江苏省徐州市2021年中考数学仿真模拟试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、选择题(本大题共有8小题,每小题3分,共24分.)
-
1. 下列说法错误的是( )A、-2的相反数是2 B、3的倒数是 C、(-3)-(-5)=2 D、-11,0,4这三个数中最小的数是02. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 有两根小棒,分别长是11厘米和16厘米,丹丹准备用一根小棒与它们围成一个三角形,她准备小棒的长可能是( )厘米.A、5 B、25 C、27 D、304. 在一个不透明的口袋中装有5个黑棋子和若干个白棋子,它们除颜色外完全相同,小明与他的朋友经过多次摸棋子试验后,发现摸到白色棋子的频率稳定在 附近,则口袋中白色棋子的个数可能是( )A、 个 B、 个 C、 个 D、 个5. 本学期某校举行了四次数学测试,李娜同学四次的成绩(单位:分)分别为80,70,90,70,王玥同学四次的成绩分别为80, ,70,90,且李娜同学四次成绩的中位数比王玥同学四次成绩的中位数少5分,则下列说法正确的是( ).A、a的值为70 B、两位同学成绩的平均数相同 C、李娜同学成绩的众数比王玥同学成绩的众数大 D、王玥同学的成绩比李娜同学的成绩稳定6. 下列运算正确的( )
3. 有两根小棒,分别长是11厘米和16厘米,丹丹准备用一根小棒与它们围成一个三角形,她准备小棒的长可能是( )厘米.A、5 B、25 C、27 D、304. 在一个不透明的口袋中装有5个黑棋子和若干个白棋子,它们除颜色外完全相同,小明与他的朋友经过多次摸棋子试验后,发现摸到白色棋子的频率稳定在 附近,则口袋中白色棋子的个数可能是( )A、 个 B、 个 C、 个 D、 个5. 本学期某校举行了四次数学测试,李娜同学四次的成绩(单位:分)分别为80,70,90,70,王玥同学四次的成绩分别为80, ,70,90,且李娜同学四次成绩的中位数比王玥同学四次成绩的中位数少5分,则下列说法正确的是( ).A、a的值为70 B、两位同学成绩的平均数相同 C、李娜同学成绩的众数比王玥同学成绩的众数大 D、王玥同学的成绩比李娜同学的成绩稳定6. 下列运算正确的( )
A、(b2)3=b5 B、x3÷x3=x C、5y3•3y2=15y5 D、a+a2=a37. 已知∠BAC=45。 , 一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )A、0<x≤1 B、 1≤x<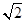 C、 0<x≤
C、 0<x≤ 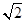 D、 x>
D、 x> 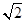 8. 如图,已知在平面直角坐标系 中,直线 分别交 轴, 轴于点 和点 ,分别交反比例函数 ( , ), ( )的图象于点 和点 ,过点 作 轴于点 ,连结 , ,若 的面积与 的面积相等,则 的值是( )
8. 如图,已知在平面直角坐标系 中,直线 分别交 轴, 轴于点 和点 ,分别交反比例函数 ( , ), ( )的图象于点 和点 ,过点 作 轴于点 ,连结 , ,若 的面积与 的面积相等,则 的值是( )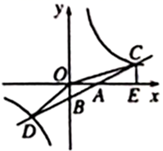 A、2 B、 C、1 D、
A、2 B、 C、1 D、二、填空题(本大题共10小题,每小题3分,共30分.)
-
9. 的算术平方根是 .10. 因式分解:x3﹣25x .11. 若式子 有意义,那么x的取值范围是 。12. 埃是表示极小长度的单位名称,是为纪念瑞典物理学家埃基特朗而定的.1埃等于一亿分之一厘米,请用科学记数法表示1埃等于 厘米.13.
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若CD=2EF=4,BC= , 则∠C等于° .
 14. 如果一个圆锥的主视图是等边三角形,俯视图是面积为4π的圆,那么它的左视图的高是 .15. 分式方程 无解,则 的值为16. 如图,点A , B , C在 上,点D在 内,则 .(填“>”,“=”或“<”)
14. 如果一个圆锥的主视图是等边三角形,俯视图是面积为4π的圆,那么它的左视图的高是 .15. 分式方程 无解,则 的值为16. 如图,点A , B , C在 上,点D在 内,则 .(填“>”,“=”或“<”)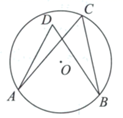 17.
17.如图,下图是一组由菱形和矩形组成的有规律的图案,第1个图中菱形的面积为S(S为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,依此类推…,则第n个图中阴影部分的面积可以用含n的代数式表示为 . (n≥2,且n是正整数)
 18. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .
18. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .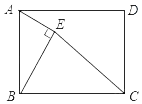
三、解答题(本大题共有10小题,共86分.)
-
19.(1)、计算:(π﹣2016)0+6cos45°﹣|﹣ |+( )﹣2(2)、先化简,再求值:( )÷ ,其中x= .20.(1)、解方程:x2+3x-2=0;(2)、解不等式组:21. 2020年元且,某商场为促销举办抽奖活动.规则如下:在一个不透明的纸盒里,装有2个红球和2个黑球,这些球除颜色外都相同.顾客每次摸出1个球,若摸到红球,则获得一份奖品;若摸到黑球,则没有奖品.(1)、如果张大妈只有一次摸球机会,那么张大妈获得奖品的概率是.(2)、如果张大妈有两次摸球机会(摸出后不放回),请用“树状图”或“列表”的方法,求张大妈获得两份奖品的概率.22. 某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人,投票结果统计如图(1);其次,对三名候选人进行了笔试和面试两项测试,各项成绩如下表所示;图(2)是某同学根据右下表绘制的一个不完整的条形图.
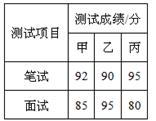
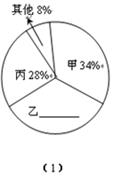
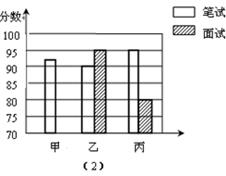
请你根据以上信息解答下列问题:
(1)、补全图(1)和图(2);(2)、请计算每名候选人的得票数;(3)、若每名候选人得一票记1分,投票、笔试、面试三项得分按照2 5 3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?23. 如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'.设旋转角为α,此时点B′恰好落在边AD上,连接B'B . (1)、当B'恰好是AD中点时,此时α=;(2)、若∠AB'B=75°,求旋转角α及AB的长.24. 2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
(1)、当B'恰好是AD中点时,此时α=;(2)、若∠AB'B=75°,求旋转角α及AB的长.24. 2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
25. 海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值) 26. 如图,在平面直角坐标系xOy中,函数 的图象与一次函数y=kx-k的图象的交点为A(m,2).
26. 如图,在平面直角坐标系xOy中,函数 的图象与一次函数y=kx-k的图象的交点为A(m,2).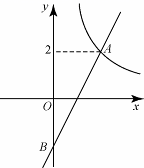 (1)、求一次函数的解析式;(2)、设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点, 且满足△PAB的面积是4,直接写出点P的坐标.27. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)、求一次函数的解析式;(2)、设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点, 且满足△PAB的面积是4,直接写出点P的坐标.27. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.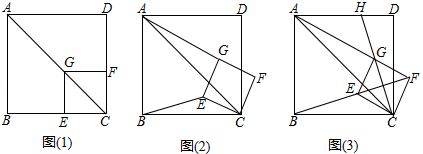 (1)、证明与推断:
(1)、证明与推断:①求证:四边形CEGF是正方形;
②推断: 的值。
(2)、探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)、拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2 ,则BC=.
28. 如图1所示,已知抛物线 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上. (1)、直接写出D点和E点的坐标;(2)、点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时, =5:6?(3)、图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、直接写出D点和E点的坐标;(2)、点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时, =5:6?(3)、图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.