初中数学苏科版七年级下册第十二章 证明 单元测试卷
试卷更新日期:2021-05-27 类型:单元试卷
一、单选题
-
1. 下列命题是真命题的是( )A、内错角相等 B、如果a2=b2 , 那么a=b C、三角形的一个外角大于任何一个内角 D、平行于同一直线的两条直线平行2. 下列命题中,正确的有( )
①两点之间线段最短;②连接两点的线段,叫做两点间的距离;③角的大小与角的两边的长短无关;④射线是直线的一部分,所以射线比直线短.
A、1个 B、2个 C、3个 D、4个3. 下列说法正确的是( )A、无限小数都是无理数 B、对顶角相等 C、图形平移后对应点所连线段平行且相等 D、两点之间垂线段最短4. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中n的值可以是( ).A、 B、 C、 D、5. 下列命题中错误的是( )A、过直线外一点有且只有一条直线与已知直线平行 B、如果两条直线都与第三条直线平行,那么这两条直线也互相平行 C、如果两条直线都与第三条直线垂直,那么这两条直线也互相垂直 D、在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条6. 如图,∠1=∠2,∠3=112°,则∠4等于( ) A、62° B、68° C、78° D、112°7. 如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( )
A、62° B、68° C、78° D、112°7. 如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( ) A、∠C=∠CDE B、∠1=∠2 C、∠3=∠4 D、∠C+∠ADC=180°8. 下列说法中错误的有( )
A、∠C=∠CDE B、∠1=∠2 C、∠3=∠4 D、∠C+∠ADC=180°8. 下列说法中错误的有( )⑴线段有两个端点,直线有一个端点;
⑵角的大小与我们画出的角的两边的长短无关;
⑶线段上有无数个点;
⑷同角或等角的补角相等;
⑸两个锐角的和一定大于直角
A、1个 B、2个 C、3个 D、4个9. 下列说法正确的是( )A、射线AB与射线BA是同一条射线 B、任何一个锐角的余角比它的补角小 C、一个角的补角一定大于这个角 D、如果 ,那么 互为补角10. 下列结论:①一个三角形的3个外角的度数之比为2:3:4,则相应的3个内角度数之比为 ;②在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;③在图形的平移中,连接对应点的线段互相平行且相等;④一个多边形的边数每增加一条,这个多边形的内角和就增加 ;⑤一个五边形最多有3个内角是直角;⑥两条直线被第三条直线所截,同旁内角的角平分线互相垂直.其中错误结论有( )A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 将“两直线平行,同位角相等”改写成“如果……那么……的形式是 。12. 请写出命题“互为相反数的两个数和为零”的逆命题:13. 命题“如果a>0,那么a2>0”的逆命题为.14. 命题“若两个角的两边互相垂直,那么这两个角相等”是命题;它的逆命题是 , 是命题.15. “两直线平行,同旁内角互补”的逆命题 , 逆命题是命题.(填“真”或“假”)16. 在△ABC中,∠A=2∠B+15°,∠C=∠A+5°,则∠B度数为 .17. 已知 ,则 的值是 .18. 已知 , ,则 .
三、解答题
-
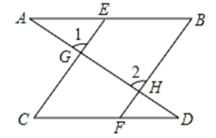
19. 如图,直线AD分与直线BE、直线CE、直线CF、直线BF相交于点A、G、D、H,且∠1=∠2,∠B=∠C.请问:AB∥CD吗?试说明理由。
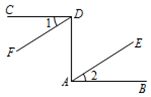
 20. 如图,AB⊥AD , CD⊥AD , ∠1=∠2,
20. 如图,AB⊥AD , CD⊥AD , ∠1=∠2,求证:DF∥EA .
 21. 补全解答过程:
21. 补全解答过程:如图,EF∥AD,∠1=∠2,若∠BAC=70°,求∠AGD.

解:∵EF∥AD,(已知)
∴∠2= , (两直线平行,同位角相等).
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥ , ()
∴∠AGD+∠BAC=180°.()
∵∠BAC=70°,(已知)
∴∠AGD= .
22. 如图, 于点D, 于点G,若 ,试说明: .下面是推理过程,请将推理过程补充完整.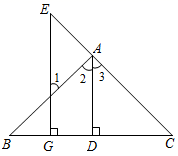
∵ 于点D, 于点G(已知),
∴ ()
∴ ()
∴ ()
∵ (已知),
∴ (等量代换)
又∵ (已证),
∴ ()
∴ (等量代换).
23. 完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.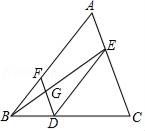
证明:∵DE∥AB(已知),
∴∠A=∠CED()
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD()
∴DF∥AE()
∴∠EGF+∠AEG=180°()
24. 如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE ∥ AB,连接AE,∠B=∠E.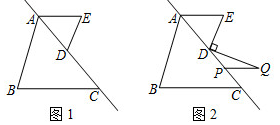 (1)、试说明AE ∥ BC.(2)、将线段AE沿着直线AC平移得到线段PQ,如图2,连接DQ.若 = ,当DE⊥DQ时,求∠Q的度数.25. 如图,∠ABC和∠BCD的平分线交于点P,延长CP交AB于点Q,且∠PBC+∠PCB=90°.
(1)、试说明AE ∥ BC.(2)、将线段AE沿着直线AC平移得到线段PQ,如图2,连接DQ.若 = ,当DE⊥DQ时,求∠Q的度数.25. 如图,∠ABC和∠BCD的平分线交于点P,延长CP交AB于点Q,且∠PBC+∠PCB=90°.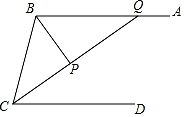 (1)、求证:AB∥CD.(2)、探究∠PBC与∠PQB的数量关系.26. 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)、求证:AB∥CD.(2)、探究∠PBC与∠PQB的数量关系.26. 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质来求∠APC.
 (1)、按小明的思路,易求得∠APC的度数为度;(2)、如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(1)、按小明的思路,易求得∠APC的度数为度;(2)、如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)、在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.