人教版2019选修三第六章计数原理单元测试

试卷更新日期：2021-05-27 类型：单元试卷

进入出卷网下载

一、单选题

1. 四个同学排成一排，甲只能排两端，共有多少种不同的排法？（）

A、6 B、12 C、24 D、30

查看试题解析
2. 若 ${(x + 1)}^{7} = a_{0} + a_{1} (x + 2) + a_{2} {(x + 2)}^{2} + \dots + a_{7} {(x + 2)}^{7}$ ，则 $a_{3} + a_{4} =$ （）．

A、0 B、35 C、70 D、-70

查看试题解析
3. 2015年11月23日，中共中央政治局审议通过《关于打赢脱贫攻坚战的决定》，在脱贫攻坚战的过程中，某单位从7名申请人中挑选5名工作人员到甲､乙两个贫困村做志愿者，要求甲村安排2名，乙村安排3名，则不同的安排方法共有（）

A、270种 B、240种 C、210种 D、180种

查看试题解析
4. 甲、乙、丙、丁和戊5名学生进行劳动技术比赛，决出第1名到第5名的名次．甲、乙两名参赛者去询问成绩，回答者对甲说：“很遗憾，你和乙都没有得到冠军”；对乙说：“你当然不会是最差的”，则该5人可能的排名情况种数为（）

A、18 B、36 C、54 D、64

查看试题解析
5. 某一次乒乓球赛的参赛队共有5小组，每小组3队.首先每小组中各队进行单循环比赛(即每两队比赛一次)，然后各小组的第一名再进行单循环比赛，则先后比赛的总次数为（）

A、15 B、20 C、25 D、30

查看试题解析
6. 在象棋比赛中，参赛的任意两位选手都比赛一场，其中胜者得2分，负者得0分，平局各得1分.现有四名学生分别统计全部选手的总得分为131分，132分，133分，134分，但其中只有一名学生的统计结果是正确的，则参赛选手共有（）

A、11位 B、12位 C、13位 D、14位

查看试题解析
7. 已知 ${(x^{2} + \frac{1}{x})}^{n} (n \in N^{*})$ 的展开式中有常数项，则 $n$ 的值可能是（）

A、5 B、6 C、7 D、8

查看试题解析
8. 从集合{A，B，C，D，E，F}和{1，2，3，4，5，6，7，8，9}中各任取2个元素排成一排（字母和数字均不能重复）．则每排中字母C和数字4，7至少出现两个的不同排法种数为（　　）

A、85 B、95 C、2040 D、2280

查看试题解析

二、多选题

9. 关于 ${(1 - 2 x)}^{2021} = a_{0} + a_{1} \cdot x + a_{2} \cdot x^{2} + \dots + a_{2001} \cdot x^{2021} (x \in R)$ ，则（）

A、 $a_{0} = 1$ B、 $a_{1} + a_{2} + a_{3} + \dots + a_{2021} = 3^{2021}$ C、 $a_{3} = 8 C_{2021}^{3}$ D、 $a_{1} - a_{2} + a_{3} - a_{4} + \dots + a_{2021} = 1 - 3^{2021}$

查看试题解析
10. 在100件产品中，有98件合格品，2件不合格品，从这100件产品中任意抽出3件，则下列结论正确的有（）

A、抽出的3件产品中恰好有1件是不合格品的抽法有 $C_{2}^{1} C_{98}^{2}$ 种 B、抽出的3件产品中恰好有1件是不合格品的抽法有 $C_{2}^{1} C_{99}^{2}$ 种 C、抽出的3件中至少有1件是不合格品的抽法有 $C_{2}^{1} C_{98}^{2} + C_{2}^{2} C_{98}^{1}$ 种 D、抽出的3件中至少有1件是不合格品的抽法有 $C_{100}^{3} - C_{98}^{3}$ 种

查看试题解析
11. 2020年3月，为促进疫情后复工复产期间安全生产，滨州市某医院派出甲、乙、丙、丁4名医生到 $A$ ， $B$ ， $C$ 三家企业开展“新冠肺炎”防护排查工作，每名医生只能到一家企业工作，则下列结论正确的是（）

A、若 $C$ 企业最多派1名医生，则所有不同分派方案共48种 B、若每家企业至少分派1名医生，则所有不同分派方案共36种 C、若每家企业至少分派1名医生，且医生甲必须到 $A$ 企业，则所有不同分派方案共12种 D、所有不同分派方案共 $4^{3}$ 种

查看试题解析
12. 某学生想在物理、化学、生物、政治、历史、地理、技术这七门课程中选三门作为选考科目，下列说法错误的是（）

A、若任意选择三门课程，选法总数为 $A_{7}^{3}$ B、若物理和化学至少选一门，选法总数为 $C_{2}^{1} C_{5}^{2}$ C、若物理和历史不能同时选，选法总数为 $C_{7}^{3} - C_{5}^{1}$ D、若物理和化学至少选一门，且物理和历史不能同时选，选法总数为 $C_{2}^{1} C_{5}^{2} - C_{5}^{1}$

查看试题解析

三、填空题

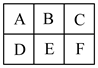
13. 5个不同的小球全部放入编号为2、3、4的三个盒子中，要求没有空盒，且每盒的小球数不大于盒子的编号数，共有种放法(用数字作答)

查看试题解析
14. $(x - 2 y) {(- x + y)}^{5}$ 展开式中，含 $x^{3} y^{3}$ 项的系数为．

查看试题解析
15. 有2辆不同的红色车和2辆不同的黑色车要停放在如图所示的六个车位中的四个内，要求相同颜色的车不在同一行也不在同一列，则共有种不同的停放方法．（用数字作答）

查看试题解析
16. 某系列智能手机玻璃版有“星河银”、“罗兰紫”、“翡冷翠”、“亮黑色”四种颜色.若甲、乙等四位市民准备分别购买一部颜色互不相同的同一型号玻璃版的该系列手机，若甲购买“亮黑色”或“星河银”，则乙不购买“罗兰紫”，则这四位市民不同的购买方案有种.

查看试题解析

四、解答题

17. 已知 ${(2 x - 1)}^{n} (n \in N^{*})$ 的二项展开式中二项式系数之和为256.

(1)、求n的值；

(2)、求该展开式中 $x^{3}$ 项的系数.

查看试题解析
18. 7人排成一排照相，按下列情况各有多少种不同的排法？

(1)、甲、乙、丙3人相邻

(2)、甲、乙、丙3人不相邻

查看试题解析
19. 盒子内有3个不同的黑球，5个不同的白球.

(1)、从中取出3个黑球、4个白球排成一列且4个白球两两不相邻的排法有多少种？

(2)、从中任取6个球且白球的个数不比黑球个数少的取法有多少种？

查看试题解析
20. 某市第一批支援湖北抗疫医疗队共10人，其中有2名志愿者、3名医生、5名护士，现根据需要，从中选派3名队员到J医院参与救治工作.

(1)、求志愿者、医生、护士各选1人的概率；

(2)、求至少选1名医生的概率.

查看试题解析
21. 为弘扬我国古代的“六艺”文化，某夏令营主办单位计划利用暑期开设“礼”、“乐”、“射”、“御”、“书”、“数”六门体验课程.

(1)、若体验课连续开设六周，每周一门，求其中“射”不排在第一周，“数”不排在最后一周的所有可能排法种数；

(2)、甲、乙、丙、丁、戊五名教师在教这六门课程，每名教师至少任教一门课程，求其中甲不任教“数”的课程安排方案种数.

查看试题解析
22. 已知4名学生和2名教师站在一排照相，求：

(1)、中间二个位置排教师，有多少种排法？

(2)、两名教师不能相邻的排法有多少种？

(3)、两名教师不站在两端，且必须相邻，有多少种排法？

查看试题解析

人教版2019选修三第六章 计数原理 单元测试

一、单选题

二、多选题

三、填空题

四、解答题

人教版2019选修三第六章计数原理单元测试