江苏省常州市2021年中考数学仿真模拟试卷
试卷更新日期:2021-05-27 类型:中考模拟
一、选择题
-
1. 的相反数为A、 B、3 C、 D、2. 下列运算不正确的是( )A、 B、 C、 D、3. 如果某物体的三视图是如图所示的三个图形,
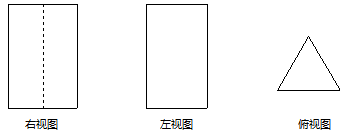
那么该物体的形状是( )
A、正方体 B、长方体 C、三棱柱 D、圆锥4. ﹣27的立方根与 的算术平方根的和是( )A、0 B、6 C、6或﹣12 D、0或65. 已知实数a,b满足 ,则下列选项错误的是( )A、 B、 C、 D、6. 如图,∠1=57°,则∠2的度数为( )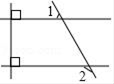 A、120° B、123° C、130° D、147°7. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A、120° B、123° C、130° D、147°7. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( ) A、1 B、1.5 C、2 D、2.58. 在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标 ,顶点 恰好落在第一象限的双曲线上,则该双曲线的解析式为( )
A、1 B、1.5 C、2 D、2.58. 在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标 ,顶点 恰好落在第一象限的双曲线上,则该双曲线的解析式为( )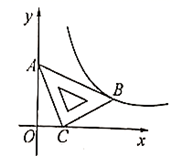 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: –2cos60°=.10. 当x时,二次根式 有意义.11. 五一假期,连云港市接待旅游总人数1760000人次,将1760000用科学记数法表示.12. 因式分解: .13. 已知一次函数y=2x﹣1的图象经过A(x1 , 1),B(x2 , 3)两点,则x1x2(填“>”“<”或“=”).14. 若m是方程 的一个根,则代数式 的值为.15. 如图所示ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=cm.
 16. 如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是.
16. 如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是. 17. 如图,已知A(4,0),B(3,3),以OA、AB为边作▱OABC , 则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为 .
17. 如图,已知A(4,0),B(3,3),以OA、AB为边作▱OABC , 则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为 .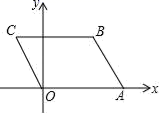 18. 如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 时,线段 的长为 .
18. 如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 时,线段 的长为 .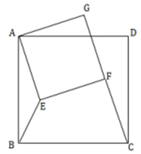
三、解答题
-
19. 先化简,再求值: ,其中 ,20.(1)、解方程 =2;(2)、解不等式组 .21. 某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20
21
19
16
27
18
31
29
21
22
25
20
19
22
35
33
19
17
18
29
18
35
22
15
18
18
31
31
19
22
整理上面数据,得到条形统计图:

样本数据的平均数、众数、中位数如下表所示:
统计量
平均数
众数
中位数
数值
23
m
21
根据以上信息,解答下列问题:
(1)、上表中众数m的值为;
(2)、为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)、该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
22. 将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.(1)、随机地抽取一张,求P(奇数);(2)、随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是“32”的概率为多少?23. 如图,已知 , ,AC与BD交于O, .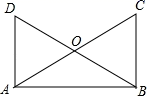
求证:
(1)、 ;(2)、 .24. 为了丰富学生的大课间活动,振海中学到体育用品商店购买篮球和足球,若购买2个篮球和3个足球共需600元,购买3个篮球和1个足球共需550元.(1)、求篮球和足球的单价分别是多少元?(2)、振海中学决定购买篮球和足球共20个,经商议,体育用品商店决定篮球单价打八折,足球单价不变,若总费用不超过2200元,那么该校最多可以购买多少个篮球?25. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .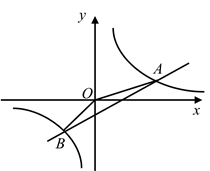 (1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.26. 如图,在△ABC中,∠C=90°,AD平分∠BAC,
(1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.26. 如图,在△ABC中,∠C=90°,AD平分∠BAC,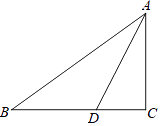 (1)、求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)(2)、求证:BC是⊙O切线.(3)、若BD=5,DC=3,求AC的长.27. 在平面直角坐标系xOy中,⊙C的半径为r(r>1),点P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:过圆心C的任意直线CP与⊙C交于点A,B,若满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图点P为⊙C的一个“完美点”.
(1)、求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)(2)、求证:BC是⊙O切线.(3)、若BD=5,DC=3,求AC的长.27. 在平面直角坐标系xOy中,⊙C的半径为r(r>1),点P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:过圆心C的任意直线CP与⊙C交于点A,B,若满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图点P为⊙C的一个“完美点”.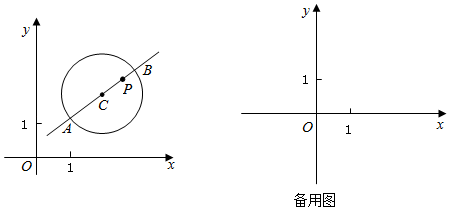 (1)、当⊙O的半径为2时
(1)、当⊙O的半径为2时①点M( ,0)⊙O的“完美点”,点(﹣ ,﹣ )⊙O的“完美点”;(填“是”或者“不是”)
②若⊙O的“完美点”P在直线y= x上,求PO的长及点P的坐标;
(2)、设圆心C的坐标为(s,t),且在直线y=﹣2x+1上,⊙C半径为r,若y轴上存在⊙C的“完美点”,求t的取值范围.28. 抛物线 与 轴交于A(4,0),B(6,0)两点,与 轴交于点C(0,3). (1)、求抛物线的解析式;(2)、点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).
(1)、求抛物线的解析式;(2)、点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,△PDE的面积最大,并求出这个最大值;
②当t =2时,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请你求出点F的坐标;若不存在,请说明理由.