江苏省无锡市2021年中考数学仿真模拟试卷

试卷更新日期：2021-05-27 类型：中考模拟

进入出卷网下载

一、选择题

1. 绝对值最小的有理数的倒数是（）

A、1 B、－1 C、0 D、不存在

查看试题解析
2. 式子 $\frac{\sqrt{2x + 1}}{x - 1}$ 有意义的x的取值范围是（）

A、 $x \geq - \frac{1}{2}$ 且x≠1 B、x≠1 C、 $x \geq - \frac{1}{2}$ D、 $x> - \frac{1}{2}$ 且x≠1

查看试题解析
3. 某市3月份某一周每天的最高气温统计如表，则这组数据（最高气温）的众数与中位数分别是（）

最高气温（℃）

13

14

15

16

天数

1

3

1

2

A、14℃，14℃ B、14℃，15℃ C、16℃，14℃ D、16℃，15℃

查看试题解析
4. 若 $2 a = 3 b$ ，则 $\frac{a}{b} =$ （）

A、 $\frac{5}{2}$ B、 $\frac{5}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
5. 已知正n边形的一个内角为135°，则边数n的值是（）

A、6 B、7 C、8 D、10

查看试题解析
6. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 下列结论正确是（）

A、x⁴·x⁴=x¹⁶ B、当x<5时，分式 $\frac{x - 5}{x^{2}}$ 的值为负数 C、若x，y的值均扩大为原来的3倍，则分式 $\frac{2 y}{x^{2}}$ 的值保持不变 D、(a⁶)²÷(a⁴)³=1

查看试题解析
8. 如图，一次函数y₁＝x﹣1与反比例函数y₂＝ $\frac{2}{x}$ 的图象交于点A（2，1），B（﹣1，﹣2），则使y₁＞y₂的x的取值范围是（）

A、x＞2 B、x＞2 或﹣1＜x＜0 C、﹣1＜x＜2 D、x＞2 或x＜﹣1

查看试题解析
9. 如图， $△ A B C$ 中， $A B = A C = 4$ ，点 $D$ 在 $B C$ 边上，连接 $A D$ ，现将 $△ A C D$ 沿着 $A D$ 对折，得到 $△ A E D$ ， $D E$ 与 $A B$ 交于点 $F$ ，若 $D E ⊥ A B$ ， $\frac{D F}{A F} = \frac{1}{4}$ ，则 $B C$ 的长为（）

A、3.8 B、 $\frac{50}{13}$ C、4 D、 $\frac{64}{17}$

查看试题解析
10. 如图，正方形ABCD中，点E，F分别在边CD，BC上，且∠EAF=45°，BD分别交AE，AF于点M，N，以点A为圆心，AB长为半径画弧BD．下列结论：①DE+BF=EF；②BN²+DM²=MN²；③△AMN∽△AFE；④ $\hat{B D}$ 与EF相切；⑤EF∥MN．其中正确结论的个数是（）

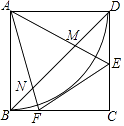A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 分解因式： $a x^{2} - 9 a =$ .

查看试题解析
12. 《战狼2》中“犯我中华者，虽远必诛”，令人动容、热血沸腾.其票房突破5600000000元，将5600000000用科学记数法表示为.

查看试题解析
13. 如图，用一个半径为60cm，圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径为cm．

查看试题解析
14. 如图，在菱形ABCD中，按以下步骤作图：
①分别以点A和B为圆心，以大于 $\frac{1}{2}$ AB的长为半径作弧，两弧相交于点E、F；

②作直线EF交BC于点G，连接AG；若AG⊥BC，CG＝3，则AD的长为．

查看试题解析
15. 若点 $(1, 5)$ , $(5, 5)$ 是抛物线 $y = {ax}^{2} + bx + c$ 上的两个点,则此抛物线的对称轴是.

查看试题解析
16. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关.”其大意是，有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为.

查看试题解析
17. 如图，D，E，F分别是边BC，AD，AC上的中点，若阴影的面积为6，则△ABC的面积是.

查看试题解析
18. 已知 $⊙ O$ 的半径 $O A = 3$ ， $B$ 为 $⊙ O$ 上一点，延长 $O B$ ，在 $O B$ 延长线上截取一点 $C$ ，使得 $B C = 2$ ， $C D$ 垂直于 $B C$ 交 $A B$ 延长线于点 $D$ ，连接 $A C$ ，若 $A C = C D$ ，则 $A B =$ .

查看试题解析

三、解答题

19.

(1)、解方程 $x^{2} - 3 x = 5 (x - 3)$

(2)、计算 $| 1 - \sqrt{2} | + 2 \cos 45 ° - \sqrt{8} + {(\frac{1}{2})}^{- 1}$

查看试题解析
20.

(1)、解不等式组 ${\begin{matrix} x - 1 < 2 x \\ \frac{x}{2} + 2 \geq 3 (x - 1) \end{matrix}$

(2)、解方程 $\frac{1}{x + 2} + \frac{4 x}{x^{2} - 4} = \frac{2}{x - 2}$ ．

查看试题解析
21. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE ，已知：∠BAC＝30°，EF⊥AB ，垂足为F ，连接DF ．

(1)、试说明AC＝EF；

(2)、求证：四边形ADFE是平行四边形．

查看试题解析
22. 小晗家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，在正常情况下，小晗按下任意一个开关均可打开对应的一盏电灯，既可三盏、两盏齐开，也可分别单盏开．因刚搬进新房不久，不熟悉情况．

(1)、若小晗任意按下一个开关，正好楼梯灯亮的概率是多少？

(2)、若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．

查看试题解析
23. 为了解学生对网上在线学习效果的满意度，某校设置了：非常满意、满意、基本满意、不满意四个选项，随机抽查了部分学生，要求每名学生都只选其中的一项，并将抽查结果绘制成如图统计图（不完整）.
请根据图中信息解答下列问题：

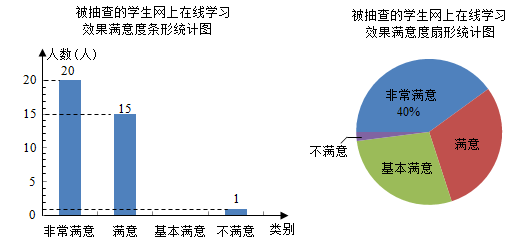(1)、求被抽查的学生人数，并补全条形统计图；

(2)、求扇形统计图中表示“满意”的扇形的圆心角度数；

(3)、若该校共有1000名学生参与网上在线学习，根据抽查结果，试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人？

查看试题解析
24. 如图，⊙O为锐角△ABC的外接圆，半径为5.

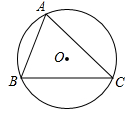(1)、用尺规作图作出∠BAC的平分线，并标出它与劣弧BC的交点E(保留作图痕迹，不写作法)；

(2)、若（1）中的点E到弦BC的距离为3，求弦CE的长.

查看试题解析
25. 如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．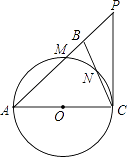

(1)、求证：直线CP是⊙O的切线；

(2)、若BC=2 $\sqrt{5}$ ，sin∠BCP= $\frac{\sqrt{5}}{5}$ ，求⊙O的半径及△ACP的周长．

查看试题解析
26. 如图，工人师傅用一块长为 $1 0dm$ ，宽为 $6 dm$ 的矩形薄铁皮，将四角各裁掉一个正方形（如图1），然后把四周折合起来成为一个体容器（如图2）．（薄铁皮厚度不计）

(1)、若长方体底面面积为 ${12dm}^{2}$ 时，裁掉的正方形边长多大？

(2)、若要求制作的长方体的底面长不大于底面宽的3倍，并将容器各面都进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，当裁掉的正方形边长多大时总费用最低，最低为多少？

查看试题解析
27. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 8 ， B C = 6 ，$ 点D在AB上， $A D = 2 ，$ 点 $E ， F$ 同时从点D出发，分别沿 $D A 、 D B$ 以每秒1个单位长度的速度向点 $A 、 B$ 匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点 $E 、 F$ 运动过程中，以EF为边作正方形EFGH使它与 $△ A B C$ 在线段AB的同铡．设 $E ， F$ 运动的时间为1秒，正方形 $E F C H$ 与 $△ A B C$ 重叠部分面积为S．

(1)、当 $0 < t < 2$ 时，求正方形EFGH的顶点刚好落在线段AC上时t的值；

(2)、当 $t \geq 2$ 时，直接写出当 $△ E G B$ 为等腰三角形时 $t$ 的值．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} - 2 a x + a^{2}$ 的顶点为A，直线 $y = x + 3$ 与抛物线交于点 $B ， C$ (点B在点C的左侧)．

(1)、求点A坐标；

(2)、横、纵坐标都是整数的点叫做整点．记线段 $B C$ 及抛物线在 $B ， C$ 两点之间的部分围成的封闭区域(不含边界)记为W．
①当 $a = 0$ 时，结合函数图象，直接写出区域W内的整点个数；

②如果区域W内有2个整点，请求出 $a$ 的取值范围．

查看试题解析

最高气温（℃）	13	14	15	16
天数	1	3	1	2