江苏省南京市2021年中考数学仿真模拟试卷(1)
试卷更新日期:2021-05-27 类型:中考模拟
一、单选题
-
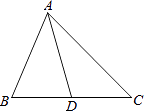
1. ( )A、±2 B、±4 C、4 D、-42. 尽管受到国际金融危机的影响,但义乌市经济依然保持了平稳增长.据统计,截止到今年4月底,我市金融机构存款余额约为1 193亿元,用科学记数法应记为( )A、1.193×1010元 B、1.193×1011元 C、1.193×1012元 D、1.193×1013元3. 化简-b•b3•(-b)4的正确结果是( )A、-b8 B、b7 C、-b7 D、b84. 下列二次根式中,能与 合并的是( )A、 B、 C、 D、5. 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
 A、 B、 C、 D、6. 一次函数y=kx+b的图像经过点( ,1)和(-1, )(m≠0),则k、b应满足的条件是( ).A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>0
A、 B、 C、 D、6. 一次函数y=kx+b的图像经过点( ,1)和(-1, )(m≠0),则k、b应满足的条件是( ).A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>0二、填空题
-
7. 函数中,自变量x的取值范围是
8. 设n为正整数,且n< <n+1,则n的值是。9. 分解因式: .10. 已知 、 是方程 的两个根,则代数式 的值为 .
11. 已知2,3,5,m,n五个数据的方差是2,那么3,4,6,m+1,n+1五个数据的方差是 .12. 如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为(结果保留根号和π). 13. 如图, 沿着直线 翻折后得到 , 沿着直线 翻折后得到 ,若 ,则 .
13. 如图, 沿着直线 翻折后得到 , 沿着直线 翻折后得到 ,若 ,则 . 14. 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为.
14. 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为.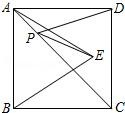 15. 如图,在同一平面直角坐标系中,若一个反比例函数的图象与正方形 交于 两点,且 两点在 轴上,点 的坐标为 ,则点F的坐标为.
15. 如图,在同一平面直角坐标系中,若一个反比例函数的图象与正方形 交于 两点,且 两点在 轴上,点 的坐标为 ,则点F的坐标为.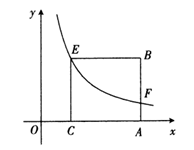 16. 如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5 ,则BC的长为 .
16. 如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5 ,则BC的长为 .
三、解答题
-
17.(1)、计算: -( )-1+4sin30°.(2)、先化简,再求值: ÷(1- ),其中m=2.18. 已知不等式组 有且只有两个整数解,求实数a的取值范围,并用数轴把它表示出来.19. 在一分钟投篮测试中,甲、乙两组同学的一次测试成绩如下:
成绩(分) 4 5 6 7 8 9 甲组(人) 1 2 4 2 1 5 乙组(人) 1 1 3 5 2 3 (1)求甲、乙两组一分钟投篮测试成绩的平均数和方差;
(2)从统计学的角度看,你认为哪组同学的测试成绩较好?为什么?20. 盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时,猜中的可能性大.请说明理由.
21. 列方程解应用题:为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车.他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?22. 直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.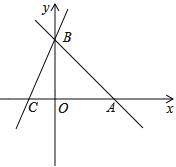 (1)、求点B的坐标;(2)、求直线BC的解析式;(3)、直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.23. 如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)、求点B的坐标;(2)、求直线BC的解析式;(3)、直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.23. 如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
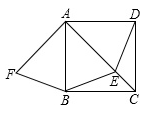 (1)、求证:BF=DE;(2)、当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.24. 如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1: , 且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.
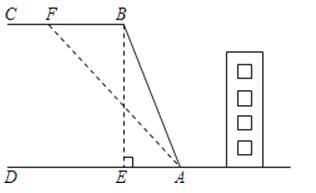
(1)、求证:BF=DE;(2)、当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.24. 如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1: , 且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长.
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75).
 25. 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H , DO及延长线分别交AC、BC于点G、.
25. 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H , DO及延长线分别交AC、BC于点G、.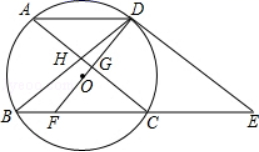 (1)、求证:DF垂直平分AC;(2)、求证:FC=CE;(3)、若弦AD=5cm , AC=8cm , 求⊙O的半径.26. 如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)、求证:DF垂直平分AC;(2)、求证:FC=CE;(3)、若弦AD=5cm , AC=8cm , 求⊙O的半径.26. 如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3). (1)、求抛物线的函数表达式;(2)、若点P在抛物线上,且 ,求点P的坐标;(3)、如图乙,设点Q是线段AC上的一动点,作DQ x轴,交抛物线于点D,求线段DQ长度的最大值.27. 如果 的两个端点 分别在 的两边上(不与点 重合),并且 除端点外的所有点都在 的内部,则称 是 的“连角弧”.(1)、图1中, 是直角, 是以 为圆心,半径为1的“连角弧”.
(1)、求抛物线的函数表达式;(2)、若点P在抛物线上,且 ,求点P的坐标;(3)、如图乙,设点Q是线段AC上的一动点,作DQ x轴,交抛物线于点D,求线段DQ长度的最大值.27. 如果 的两个端点 分别在 的两边上(不与点 重合),并且 除端点外的所有点都在 的内部,则称 是 的“连角弧”.(1)、图1中, 是直角, 是以 为圆心,半径为1的“连角弧”.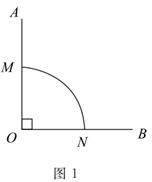
①图中 的长是 , 并在图中再作一条以 为端点、长度相同的“连角弧”;
②以 为端点,弧长最长的“连角弧”的长度是 .
(2)、如图2,在平面直角坐标系 中,点 ,点 在 轴正半轴上,若 是半圆,也是 的“连角弧”,求 的取值范围.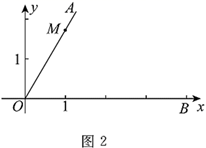 (3)、如图3,已知点 分别在射线 上, 是 的“连角弧”,且 所在圆的半径为 ,直接写出 的取值范围.
(3)、如图3,已知点 分别在射线 上, 是 的“连角弧”,且 所在圆的半径为 ,直接写出 的取值范围.