广东省揭阳市普宁市2019-2020学年高一下学期数学期末考试试卷

试卷更新日期：2021-05-26 类型：期末考试

进入出卷网下载

一、单选题

1. 若集合 $A = {x | - 2 < x < 1}$ ， $B = {x | x < - 1$ 或 $x > 3}$ ，则 $A \cap B =$ （）

A、 ${x | - 1 < x < 1}$ B、 ${x | 1 < x < 3}$ C、 ${x | - 2 < x < - 1}$ D、 ${x | - 2 < x < 3}$

查看试题解析
2. 为了检查某超市货架上的饮料是否含有塑化剂，要从编号依次为1到50的塑料瓶装饮料中抽取5瓶进行检验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的5瓶饮料的编号可能是（）

A、5，10，15，20，25 B、2，4，6，8，10 C、1，2，3，4，5 D、7，17，27，37，47

查看试题解析
3. 现有四个函数：① $y = x \cdot \sin x$ ；② $y = x \cdot \cos x$ ；③ $y = x \cdot | \cos x |$ ；④ $y = x \cdot 2^{x}$ 的图象（部分）如下，则按照从左到右图象对应的函数序号安排正确的一组是（）

A、①④②③ B、①④③② C、④①②③ D、③④②①

查看试题解析
4. 已知 $a = 2^{1.2}$ ， $b = 2^{0.8}$ ， $c = 2 \log_{5} 2$ ，则 $a, b, c$ 的大小关系为（）．

A、 $c < b < a$ B、 $c < a < b$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析
5. 已知平面向量 $\vec{a} = (1, 2), \vec{b} = (- 2, m)$ ，且 $\vec{a} / / \vec{b}$ ，则 $2 \vec{a} + 3 \vec{b} =$ （）

A、 $(- 5, - 10)$ B、 $(- 4, - 8)$ C、 $(- 3, - 6)$ D、 $(- 2, - 4)$

查看试题解析
6. 直线 $a x + y - 1 = 0$ 与直线 $2 x + 3 y - 2 = 0$ 垂直，则实数 $a$ 的值为（）

A、 $\frac{2}{3}$ B、-1 C、-2 D、 $- \frac{3}{2}$

查看试题解析
7. 某校举行演讲比赛，9位评委给选手 $A$ 打出的分数如茎叶图所示，统计员在去掉一个最高分和一个最低分后，算得平均分为91，复核员在复核时，发现有一个数字(茎叶图中的 $x$ )无法看清，若统计员计算无误，则数字 $x$ 应该是（）

A、5 B、4 C、3 D、2

查看试题解析
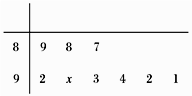8. 已知函数 $f (x) = \sin (ω x + φ)$ ( $ω > 0$ ， $| φ | < \frac{π}{2}$ )的部分图象如图所示，则（）

A、 $ω = 2$ ， $φ = \frac{π}{6}$ B、 $ω = \frac{1}{2}$ ， $φ = \frac{π}{6}$ C、 $ω = 2$ ， $φ = \frac{π}{3}$ D、 $ω = \frac{1}{2}$ ， $φ = \frac{π}{3}$

查看试题解析
9. 设甲､乙两个圆柱的底面积分别为 $S_{1}$ ､ $S_{2}$ ，体积分别为 $V_{1}$ ､ $V_{2}$ .若它们的侧面积相等，且 $\frac{S_{1}}{S_{2}} = \frac{9}{4}$ ，则 $\frac{V_{1}}{V_{2}}$ 的值是（）

A、2 B、 $\frac{3}{2}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
10. 已知圆 ${(x - a)}^{2} + y^{2} = a^{2}$ 平分圆 ${(x + 1)}^{2} + {(y - 2)}^{2} = 1$ 的周长，则a的值是（）

A、0 B、-3 C、 $- \frac{2}{5}$ D、 $\frac{5}{2}$

查看试题解析

二、多选题

11. 已知函数 $f (x) = \log_{a} | x - 1 |$ 在区间 $(- \infty, 1)$ 上单调递增，则（）

A、 $0 < a < 1$ B、 $a > 1$ C、 $f (a + 2019) > f (2020)$ D、 $f (a + 2019) < f (2020)$

查看试题解析
12. 给出如下四个表述，其中说法正确的是（）

A、存在实数 $α$ ，使得 $\sin α + \cos α = \frac{5}{3}$ B、直线 $x = 2019 π$ 是函数 $y = \cos x$ 图像的一条对称轴 C、 $y = \cos (\sin x)$ 的值域是 $[\cos 1 ， 1]$ D、若 $α$ ､ $β$ 都是第一象限角，且 $\sin α > \sin β$ ，则 $\tan α > \tan β$

查看试题解析

三、填空题

13. 已知点 $A (0, 1)$ ， $B (3, 2)$ ，向量 $\vec{A C} = (4, 3)$ ，则向量 $| \vec{B C} | =$ .

查看试题解析
14. 函数 $f (x) = x^{2} + 2 (a - 1) x + 2$ 在 $(- \infty, 4]$ 是减函数，则实数a的取值范围是

查看试题解析
15. 已知点 $A$ 在圆 $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$ 上运动，点 $B$ 在直线 $l : x - y + 2 = 0$ 上运动，且直线 $A B$ 与直线 $l$ 的夹角为 $30 °$ ，则 $A B$ 的最小值为.

查看试题解析
16. 已知 $a > 0$ 且 $a \neq 1$ ，函数 $f (x) = a^{x - 2} + 2$ 的图像恒经过的点 $P$ 的坐标为；若角 $θ$ 的终边经过点 $P$ ，则 $\sin^{2} θ - \sin 2 θ =$ .

查看试题解析

四、解答题

17. 已知函数 $f (x) = {\begin{array}{l} x - \frac{2}{x}, x > \frac{1}{2} \\ x^{2} - x + a - 1, x < \frac{1}{2} \end{array}$ ，

(1)、若 $a = 1$ ，求函数 $f (x)$ 的零点；

(2)、根据定义证明 $f (x)$ 在 $(\frac{1}{2}, + \infty)$ 上单调递增.

查看试题解析
18. 已知向量 $\vec{a} = (\sin x, \cos x)$ ， $\vec{b} = (\sqrt{3}, - 1)$ ， $x \in [0, π]$ .

(1)、若 $\vec{a} ⊥ \vec{b}$ ，求 $x$ 的值；

(2)、记 $f (x) = \vec{a} \cdot \vec{b}$ ，求 $f (x)$ 的最大值和最小值以及对应的 $x$ 的值.

查看试题解析
19. 为了了解高中新生的体能情况，某学校抽取部分高一学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12﹒

(1)、第二小组的频率是多少？样本容量是多少？

(2)、若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？

(3)、在这次测试中，学生跳绳次数的中位数落在哪个小组内？请说明理由．

查看试题解析
20. 如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是菱形， $P A = P D ， ∠ B A D = 60^{\circ} ， E$ 是 $A D$ 的中点，点 $Q$ 在侧棱 $P C$ 上．

(1)、求证： $A D ⊥$ 平面 $P B E$ ；

(2)、若 $Q$ 是 $P C$ 的中点，求证： $P A / /$ 平面 $B D Q$ ；

(3)、若 $V_{P - B C D E} = 2 V_{Q - A B C D}$ ，试求 $\frac{C P}{C Q}$ 的值．

查看试题解析
21. 在直角坐标系 $x O y$ 中，已知圆 $C : x^{2} + y^{2} - 4 x - 6 y + m = 0$ 与直线 $l : x + y - 1 = 0$ 相切，

(1)、求实数 $m$ 的值；

(2)、过点 $(3, 1)$ 的直线与圆 $C$ 交于 $M$ ､ $N$ 两点，如果 $| M N | = 2 \sqrt{3}$ ，求 $\vec{O M} \cdot \vec{O N}$ .

查看试题解析
22. 已知 $k \in R$ ，函数 $f (x) = \log_{2} (4^{x} + 1) + k x$ 是偶函数，

(1)、求 $k$ 的值；

(2)、求不等式 $f (x) > \log_{2} \frac{3}{2^{x + 1}}$ 的解集；

(3)、若函数 $g (x) = f (x) - \log_{2} (a \cdot 2^{x} - \frac{4}{3} a)$ 在 $(\log_{2} \frac{4}{3}, + \infty)$ 内存在唯一的零点，求实数 $a$ 的取值范围.

查看试题解析