初中数学苏科版八年级下册第十二章二次根式单元测试

试卷更新日期：2021-05-26 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{0.1}$ B、 $\sqrt{24}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{a^{2} + b^{2}}$

查看试题解析
2. 若代数式 $\sqrt{x - 4}$ 有意义，则x的取值范围是（）

A、x≥4 B、x=4 C、x≤4 D、x≠4

查看试题解析
3. 若等式 $\sqrt{a^{2}} = {(\sqrt{a})}^{2}$ ，成立，则实数a的取值范围是（）

A、 $a > 0$ B、 $a < 0$ C、 $a \geq 0$ D、 $a \leq 0$

查看试题解析
4. 下列计算正确的是（）

A、 $2 \sqrt{3} + 4 \sqrt{2} = 6 \sqrt{5}$ B、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ C、 $\sqrt{27} \div \sqrt{3} = 9$ . D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
5. 下列说法中正确的是（）

A、使式子 $\sqrt{x + 3}$ 有意义的是x＞﹣3 B、使 $\sqrt{12 n}$ 是正整数的最小整数n是3 C、若正方形的边长为3 $\sqrt{10}$ cm，则面积为30cm² D、计算3÷ $\sqrt{3}$ × $\frac{1}{\sqrt{3}}$ 的结果是3

查看试题解析
6. 设 $a = \sqrt{19} - 1$ ，a在两个相邻整数之间，则这两个整数是（）

A、1和2 B、2和3 C、3和4 D、4和5

查看试题解析
7. 若x ， y为实数，且y＝2+ $\sqrt{3 - x}$ + $\sqrt{x - 3}$ ，则|x+y|的值是（）

A、5 B、3 C、2 D、1

查看试题解析
8. 估计 $\sqrt{12} \times \sqrt{\frac{1}{3}} + \sqrt{10} \div \sqrt{2}$ 的运算结果应在下列哪两个数之间（）

A、3.5 和 4.0 B、4.0 和 4.5 C、4.5 和 5.0 D、5.0 和 5.5

查看试题解析
9. 已知a>b>0，并且a+b=6 $\sqrt{a b}$ ，则 $\frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} + \sqrt{b}}$ 的值为（）

A、2 B、 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
10. 已知x为实数，化简 $\sqrt{- x^{3}} - x \sqrt{- \frac{1}{x}}$ 的结果为（　　）

A、 $(x - 1) \sqrt{- x}$ B、 $(- 1 - x) \sqrt{- x}$ C、 $(1 - x) \sqrt{- x}$ D、 $(1 + x) \sqrt{- x}$

查看试题解析

二、填空题

11. 化简 $\sqrt{{(3.14 - π)}^{2}}$ ＝.

查看试题解析
12. 若 $\sqrt{{(a - 3)}^{2}} = 3 - a$ ，则a的取值范围是.

查看试题解析
13. 实数 $\frac{1}{3 - \sqrt{7}}$ 的整数部分 $a =$ ，小数部分 $b =$ ．

查看试题解析
14. 比较大小： $\frac{1}{\sqrt{6} - \sqrt{5}}$ $\frac{1}{\sqrt{7} - \sqrt{6}}$ （用 $>, <$ 或 $=$ 填空）

查看试题解析
15. 最简二次根式 $\sqrt{b + 2}$ 与 ${}^{a - 1}{\sqrt{5 - 2 b}}$ 是同类最简二次根式，则a-b=。

查看试题解析
16. 已知点P（﹣10，1）关于y轴对称点Q（a+b，b﹣1），则 $\sqrt{a} + \sqrt{b}$ 的值为.

查看试题解析
17. 已知 $y = \sqrt{x^{2} - 4 x + 4} - x + 3$ ，当 $x$ 分别取 $1, 2, 3, \dots, 2020$ 时，所对应的 $y$ 值的总和是．

查看试题解析
18. 已知实数a满足|2014-a|+ $\sqrt{a - 2015}$ =a，那么a-2014²+1的值是．

查看试题解析

三、综合题

19. 计算：

(1)、 ${(π - 2009)}^{0} + \sqrt{12} + | \sqrt{3} - 2 |$

(2)、 $(3 \sqrt{2} - \sqrt{6}) (3 \sqrt{2} + \sqrt{6}) - (\sqrt{3} - 1)$

(3)、 $\sqrt{2} - \frac{1}{\sqrt{3} - \sqrt{2}}$

(4)、 $\sqrt{18} - \frac{\sqrt{3} + \sqrt{6}}{\sqrt{3}} + \sqrt{{(1 + \sqrt{2})}^{2}}$

查看试题解析
20. 已知 $a ， b ， c$ 实数在数轴上的对应点如图所示，化简 $\sqrt{a^{2}} - | a - b | + | c - a | + \sqrt{{(b - c)}^{2}}$

查看试题解析
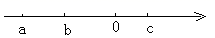21. 已知2a-1的平方根是 $\pm$ 3,3a+b-9的立方根是2，c是 $\sqrt{57}$ 的整数部分，求a+2b+c的算数平方根。

查看试题解析
22. 已知 $y = \sqrt{2 x - 5} - \sqrt{5 - 2 x} + 3$ ，求 $(2 \sqrt{x} + \sqrt{y}) (2 \sqrt{x} - \sqrt{y})$ 的值.

查看试题解析
23. 我们将 $(\sqrt{a} + \sqrt{b})$ 、 $(\sqrt{a} - \sqrt{b})$ 称为一对“对偶式”，因为 $(\sqrt{a} + \sqrt{b}) (\sqrt{a} - \sqrt{b}) = {(\sqrt{a})}^{2} - {(\sqrt{b})}^{2}$ $= a - b$ ，所以构造“对偶式”再将其相乘可以有效的将 $(\sqrt{a} + \sqrt{b})$ 和 $(\sqrt{a} - \sqrt{b})$ 中的“ ”去掉.于是二次根式除法可以这样解：如 $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{2 + \sqrt{2}}{2 - \sqrt{2}} = \frac{{(2 + \sqrt{2})}^{2}}{(2 + \sqrt{2}) \times (2 - \sqrt{2})} = 3 +$ $2 \sqrt{2}$ ．像这样，通过分子，分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化.根据以上材料，理解并运用材料提供的方法，解答以下问题：

(1)、比较大小 $\frac{1}{\sqrt{7} - 2}$ $\frac{1}{\sqrt{6} - \sqrt{3}}$ （用“ $>$ ”、“ $<$ ”或“ $=$ ”填空）；

(2)、已知 $x = \frac{\sqrt{5} + 2}{\sqrt{5} - 2}$ ， $y = \frac{\sqrt{5} - 2}{\sqrt{5} + 2}$ ，求 $x^{2} + y^{2}$ 的值；

(3)、计算： $\frac{2}{3 + \sqrt{3}} + \frac{2}{5 \sqrt{3} + 3 \sqrt{5}} + \frac{2}{7 \sqrt{5} + 5 \sqrt{7}} + \dots \dots + \frac{2}{99 \sqrt{97} + 97 \sqrt{99}}$

查看试题解析
24. 观察下列各式及其验算过程：
$\sqrt{2 + \frac{2}{3}}$ =2 $\sqrt{\frac{2}{3}}$ ，验证： $\sqrt{2 + \frac{2}{3}}$ = $\sqrt{\frac{2 \times 3 + 2}{3}}$ = $\sqrt{\frac{2^{3}}{3}}$ =2 $\sqrt{\frac{2}{3}}$ ；
$\sqrt{3 + \frac{3}{8}}$ =3 $\sqrt{\frac{3}{8}}$ ，验证： $\sqrt{3 + \frac{3}{8}}$ = $\sqrt{\frac{8 \times 3 + 3}{8}}$ = $\sqrt{\frac{3^{3}}{8}}$ =3 $\sqrt{\frac{3}{8}}$

(1)、按照上述两个等式及其验证过程的基本思路，猜想 $\sqrt{4 + \frac{4}{15}}$ 的变形结果并进行验证．

(2)、针对上述各式反映的规律，写出用n（n为大于1的整数）表示的等式并给予验证．

查看试题解析
25. 阅读理解：
求 $\sqrt{3 + \sqrt{5}} + \sqrt{3 - \sqrt{5}}$ 的值．

解：

设 $x = \sqrt{3 + \sqrt{5}} + \sqrt{3 - \sqrt{5}}$

两边平方得： $x^{2} = {(\sqrt{3 + \sqrt{5}})}^{2} + {(\sqrt{3 - \sqrt{5}})}^{2} + 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})}$

∴ $x^{2} = 3 + \sqrt{5} + 3 - \sqrt{5} + 4$ ，即 $x^{2} = 10$ .

∴ $x = \pm \sqrt{10}$

∵ $\sqrt{3 + \sqrt{5}} + \sqrt{3 - \sqrt{5}} > 0$

∴ $\sqrt{3 + \sqrt{5}} + \sqrt{3 - \sqrt{5}} = \sqrt{10}$

请利用上述方法，求 $\sqrt{4 + \sqrt{7}} + \sqrt{4 - \sqrt{7}}$ 的值．

查看试题解析
26. 阅读材料：
基本不等式 $\sqrt{a b}$ ≤ $\frac{a + b}{2}$ （a＞0，b＞0），当且仅当a＝b时等号成立，它是解决最值问题的有力工具.

例如：在x＞0的条件下，当x为何值时，x+ $\frac{1}{x}$ 有最小值，最小值是多少？

解：∵x＞0， $\frac{1}{x}$ ＞0∴ $\frac{x + \frac{1}{x}}{2}$ ≥ $\sqrt{x \cdot \frac{1}{x}}$ ，即 $x + \frac{1}{x}$ ≥2 $\sqrt{x \cdot \frac{1}{x}}$ ，∴ $x + \frac{1}{x}$ ≥2

当且仅当x＝ $\frac{1}{x}$ ，即x＝1时，x+ $\frac{1}{x}$ 有最小值，最小值为2.

请根据阅读材料解答下列问题：

(1)、已知x＞0，则当x为时，代数式3x+ $\frac{3}{x}$ 的最小值为；

(2)、已知a＞0，b＞0，a²+b²=7，则ab的最大值为

(3)、已知矩形面积为9，求矩形周长的最小值.

查看试题解析
27. 阅读下列材料，解答后面的问题：我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积.用现代式子表示即为： $S = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ ……①（其中 $a$ 、 $b$ 、 $c$ 为三角形的三边长， $s$ 为面积）.而另一个文明古国古希腊也有求三角形面积的“海伦公式”： $S = \sqrt{p (p - a) (p - b) (p - c)}$ ……②（其中 $p = \frac{a + b + c}{2}$ ）

(1)、若已知三角形的三边长分别为3，5，6，试分别运用公式①和公式②计算该三角形的面积 $s$ ；

(2)、你能否由公式①推导出公式②？请试试写出推导过程.

查看试题解析

初中数学苏科版八年级下册第十二章 二次根式 单元测试

一、单选题

二、填空题

三、综合题

初中数学苏科版八年级下册第十二章二次根式单元测试