苏科版备考2021年中考数学三轮冲刺专题9 函数综合问题
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
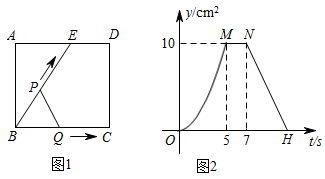
1. 如图1,已知E为矩形ABCD的边AD上的一点,动点P,Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止;点Q沿BC运动到点C时停止,它们运动的速度都是1cm/s.设P,Q同时出发,t(s)时,△BPQ的面积为y( ).已知y与t的函数关系图象如图2(曲线OM为抛物线的一部分),有下列结论:①AD=BE=5cm;② ;③当 时, ;④当 时,△ABE∽△QBP其中正确的结论是( )
 A、①② B、③④ C、①③④ D、①②③④2. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③m(am+b)+b≤a;④(a+c)2<b2;其中正确结论的个数有( )个.
A、①② B、③④ C、①③④ D、①②③④2. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③m(am+b)+b≤a;④(a+c)2<b2;其中正确结论的个数有( )个.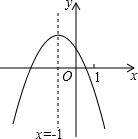 A、1个 B、2个 C、3个 D、43. 如图,反比例函数 (x>0)的图象经过□OABC的顶点C和对角线的交点E,顶点A在x轴上,若□OABC的面积为18,则k的值为( )
A、1个 B、2个 C、3个 D、43. 如图,反比例函数 (x>0)的图象经过□OABC的顶点C和对角线的交点E,顶点A在x轴上,若□OABC的面积为18,则k的值为( )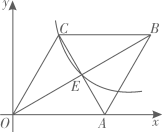 A、8 B、6 C、4 D、24. 成都市双流新城公园是亚洲最大的城市湿地公园,周末小李在这个公园里某笔直的道路上骑车游玩,先前进了a千米,休息了一段时间,又原路返回b千米(b<a),再前进c千米,则他离起点的距离s与时间t的关系的示意图是( )A、
A、8 B、6 C、4 D、24. 成都市双流新城公园是亚洲最大的城市湿地公园,周末小李在这个公园里某笔直的道路上骑车游玩,先前进了a千米,休息了一段时间,又原路返回b千米(b<a),再前进c千米,则他离起点的距离s与时间t的关系的示意图是( )A、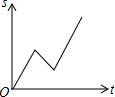 B、
B、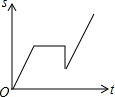 C、
C、 D、
D、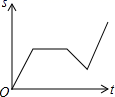 5. 如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y2>y1 , 则自变量x的取值范围是( )
5. 如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y2>y1 , 则自变量x的取值范围是( )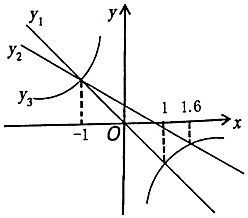 A、x<﹣1 B、﹣1<x<0或x>1.6 C、﹣1<x<0 D、x<﹣1或0<x<16. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、7. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( )
A、x<﹣1 B、﹣1<x<0或x>1.6 C、﹣1<x<0 D、x<﹣1或0<x<16. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、7. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( ) A、A→O→B B、B→A→C C、B→O→C D、C→B→O8. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A、A→O→B B、B→A→C C、B→O→C D、C→B→O8. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )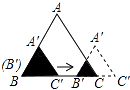 A、
A、 B、
B、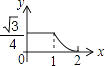 C、
C、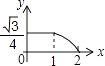 D、
D、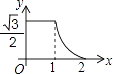 9. 已知二次函数y=x2﹣2x+c的图象沿x轴平移后经过(﹣1,y1),(5,y2)两点若y1>y2 , 则图象可能的平移方式是( )
9. 已知二次函数y=x2﹣2x+c的图象沿x轴平移后经过(﹣1,y1),(5,y2)两点若y1>y2 , 则图象可能的平移方式是( )
A、向左平移5单位 B、向左平移3单位 C、向右平移1单位 D、向右平移2单位10. 在平面直角坐标系xOy中,过点A(﹣5,0)作垂直于x轴的直线AB,直线y=x+b与双曲线y=﹣ 相交于点P(x1 , y1)、Q(x2 , y2),与直线AB相交于点R(x3 , y3).若y1>y2>y3时,则b的取值范围是( )A、b>4 B、b>4或b<﹣4 C、﹣ <b<﹣4或b>4 D、4<b< 或b<﹣4二、填空题
-
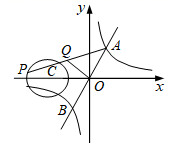
11. 如图,一次函数 = 与反比例函数 = ( >0)的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为 ,则 的值为.
 12. 如图,平面直角坐标系中,点 , ,若抛物线 与线段AB(包含A、B两点)有两个不同交点,则a的取值范围是.
12. 如图,平面直角坐标系中,点 , ,若抛物线 与线段AB(包含A、B两点)有两个不同交点,则a的取值范围是.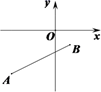 13. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是 .14. 如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE= .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 .
13. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是 .14. 如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE= .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 .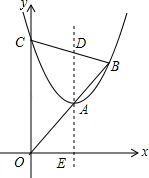 15. 若关于x的方程x2﹣2ax+a﹣2=0的一个实数根为x1≥1,另一个实数根x2≤﹣1,则抛物线y=﹣x2+2ax+2﹣a的顶点到x轴距离的最小值是.16. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是.
15. 若关于x的方程x2﹣2ax+a﹣2=0的一个实数根为x1≥1,另一个实数根x2≤﹣1,则抛物线y=﹣x2+2ax+2﹣a的顶点到x轴距离的最小值是.16. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是.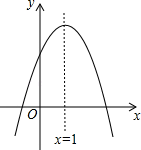 17. 如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
17. 如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .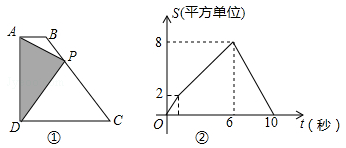 18. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .19. 如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 .
18. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .19. 如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 .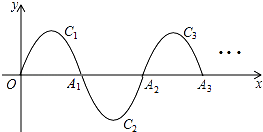 20. 如图,在平面直角坐标系中,反比例函数 与正比例函数 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是.
20. 如图,在平面直角坐标系中,反比例函数 与正比例函数 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是.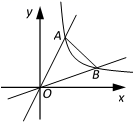
三、综合题
-
21. 已知:关于x的二次函数 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.(1)、y1=y2 , 请说明a必为奇数;(2)、设a=11,求使y1≤y2≤y3成立的所有n的值;(3)、对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.22. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.
 (1)、求抛物线的函数表达式;(2)、直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为 ,求点P,Q的坐标;(3)、在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上?若存在,请直接写出点K的坐标;若不存在,请说明理由.23. 如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC
(1)、求抛物线的函数表达式;(2)、直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为 ,求点P,Q的坐标;(3)、在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上?若存在,请直接写出点K的坐标;若不存在,请说明理由.23. 如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC (1)、求线段OC的长度;(2)、设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;(3)、在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.24. 如图,点A是直线y=﹣2x与反比例函数y= (m为常数)的图象的交点.过点A作x轴的垂线,垂足为B,且OB=2.
(1)、求线段OC的长度;(2)、设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;(3)、在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.24. 如图,点A是直线y=﹣2x与反比例函数y= (m为常数)的图象的交点.过点A作x轴的垂线,垂足为B,且OB=2.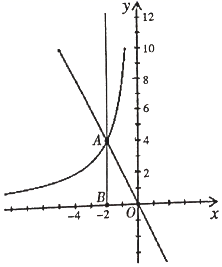 (1)、求点A的坐标及m的值;(2)、已知点P(0,n)(0<n≤10),过点P作平行于x轴的直线,交直线y=﹣2x于点C(x1 , y1),交反比例函数y= (m为常数)的图象于点D(x2 , y2),交垂线AB于点E(x3 , y3),若x1<x3<x2 , 结合函数的图象,直接写出x1+x2+x3的取值范围.25. 疫情期间,某销售商在网上销售A、B两种型号的电脑“手写板”,其进价、售价和每日销量如下表所示:
(1)、求点A的坐标及m的值;(2)、已知点P(0,n)(0<n≤10),过点P作平行于x轴的直线,交直线y=﹣2x于点C(x1 , y1),交反比例函数y= (m为常数)的图象于点D(x2 , y2),交垂线AB于点E(x3 , y3),若x1<x3<x2 , 结合函数的图象,直接写出x1+x2+x3的取值范围.25. 疫情期间,某销售商在网上销售A、B两种型号的电脑“手写板”,其进价、售价和每日销量如下表所示:进价(元/个)
售价(元/个)
销量(个/日)
A型
400
600
200
B型
800
1200
400
根据市场行情,该销售商对A型手写板降价销售,同时对B型手写板提高售价,此时发现A型手写板每降低5元就可多卖1个,B型手写板每提高5元就少卖1个.销售时保持每天销售总量不变,设其中A型手写板每天多销售x个,每天获得的总利润为y元.
(1)、求y与x之间的函数关系式,并直接写出x的取值范围;(2)、要使每天的利润不低于212000元,求出x的取值范围;(3)、该销售商决定每销售一个B型手写板,就捐助a元 给受“新冠疫情”影响的困难学生,若当30≤x≤40时,每天的最大利润为203400元,求a的值.26. 如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
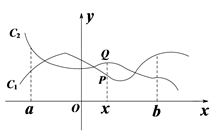 (1)、判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;(2)、若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;27. 已知二次函数y=ax2-6ax+5a(a为常数)的图象为抛物线C.(1)、求证:不论a为何值,抛物线C与x轴总有两个不同的公共点;(2)、设抛物线C交x轴于点A、B,交y轴于点D,若△ABD的面积为20,求a的值;(3)、设点E(2,4)、F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图象,直接写出a的取值范围.28. 根据完全平方公式可以作如下推导(a、b都为非负数)
(1)、判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;(2)、若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;27. 已知二次函数y=ax2-6ax+5a(a为常数)的图象为抛物线C.(1)、求证:不论a为何值,抛物线C与x轴总有两个不同的公共点;(2)、设抛物线C交x轴于点A、B,交y轴于点D,若△ABD的面积为20,求a的值;(3)、设点E(2,4)、F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图象,直接写出a的取值范围.28. 根据完全平方公式可以作如下推导(a、b都为非负数)∵ a-2 +b=( - )2≥0 ∴ a-2 +b≥0
∴ a+b≥2 ∴ ≥
其实,这个不等关系可以推广, ≥
… …
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时, ,则 有最小值.
再如:x为非负数时,x+x+ .
我们来研究函数:
 (1)、这个函数的自变量x的取值范围是;(2)、完成表格并在坐标系中画出这个函数的大致图象;
(1)、这个函数的自变量x的取值范围是;(2)、完成表格并在坐标系中画出这个函数的大致图象;x
…
-3
-2
-1
1
2
3
…
y
…
3
5
…
(3)、根据算术—几何均值不等式,该函数在第一象限有最值,是;(4)、某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .29. 平面直角坐标系中,抛物线C1:y1=x2-2mx+2m2-1,抛物线C2:y2=x2-2nx+2n2-1,(1)、若m=2,过点A(0,7)作直线l垂直于y轴交抛物线C1于点B、C两点.①求BC的长;
②若抛物线C2与直线l交于点E、F两点,若EF长大于BC的长。求出n的范围;
(2)、若m+n=k(k是常数),①若 ,试说明抛物线C1与抛物线C2的交点始终在定直线上;
②求y1+y2的最小值(用含k的代数式表示).
30. 已知,抛物线y=ax2+bx+c(a≠0)的顶点为A(s,t)(其中s≠0).(1)、若抛物线经过(2,7)和(-3,37)两点,且s=1.①求抛物线的解析式;
②若n>1,设点M(n,y1),N(n+1,y2)在抛物线上,比较y1 , y2的大小关系,并说明理由;
(2)、若a=2,c=-2,直线y=2x+m与抛物线y=ax2+bx+c的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;(3)、若点A在抛物线y= 上,且2≤s<3时,求a的取值范围.31. 如图,在平面直角坐标系中,直线 分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.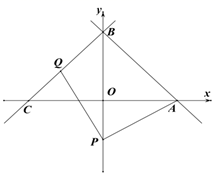 (1)、求直线BC的函数关系式;(2)、点P(0,t)在y轴负半轴上,Q为线段BC上一动点(不与B、C重合).连接PA、PQ,PQ=PA
(1)、求直线BC的函数关系式;(2)、点P(0,t)在y轴负半轴上,Q为线段BC上一动点(不与B、C重合).连接PA、PQ,PQ=PA①若点Q为BC中点,求t的值;
②用t的代数式表示点Q的坐标和直线PQ的函数关系式;
③若M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,求n的取值范围.
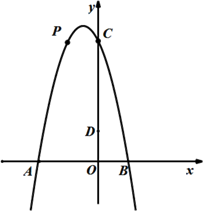
32. 如图,二次函数 的图象与 轴交于点A、B,与y轴交于点C,点B的坐标为 ,点 在y轴上,连接AD.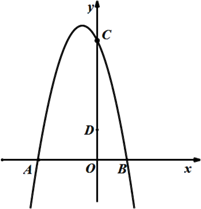
 (1)、 =;(2)、若点P是抛物线在第二象限上的点,过点 作PF⊥x轴,垂足为F, 与 交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点 的坐标;若不存在,请说明理由;(3)、若点 在抛物线上,且点 的横坐标大于-4,过点 作 ,垂足为H,直线 与 轴交于点K,且 ,求点 的坐标.33. 已知,抛物线y=ax²-2amx+am2+2m-5与x轴交于A(x1 , 0),B(x2 , 0)(x1<x2)两点,顶点为P。(1)、当a=1,m=2时,求线段AB的长度;(2)、当a=2,若点P到x轴的距离与点P到y轴的距离相等,求该抛物线的解析式;(3)、若a= ,当2m-5≤x≤2m-2时,y的最大值为2,求m的值。34. 黄冈市某高新企业制定工龄工资标准时充分考虑员工对企业发展的贡献,同时提高员工的积极性、控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.
(1)、 =;(2)、若点P是抛物线在第二象限上的点,过点 作PF⊥x轴,垂足为F, 与 交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点 的坐标;若不存在,请说明理由;(3)、若点 在抛物线上,且点 的横坐标大于-4,过点 作 ,垂足为H,直线 与 轴交于点K,且 ,求点 的坐标.33. 已知,抛物线y=ax²-2amx+am2+2m-5与x轴交于A(x1 , 0),B(x2 , 0)(x1<x2)两点,顶点为P。(1)、当a=1,m=2时,求线段AB的长度;(2)、当a=2,若点P到x轴的距离与点P到y轴的距离相等,求该抛物线的解析式;(3)、若a= ,当2m-5≤x≤2m-2时,y的最大值为2,求m的值。34. 黄冈市某高新企业制定工龄工资标准时充分考虑员工对企业发展的贡献,同时提高员工的积极性、控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄-18,
企业工龄=现年年龄-参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
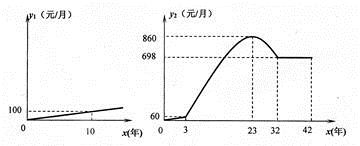 (1)、求出y1、y2与工龄x之间的函数关系式;(2)、现年28岁的高级技工小张从18岁起一直在深圳实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)、已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?35. 在平面直角坐标系xOy中,抛物线G: 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数 ( )的图像为直线 .(1)、求A、B两点的坐标;(2)、当1≤x≤2时, ≤ ≤ ,试说明:抛物线G的顶点不在直线 上;(3)、设 ,直线 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.36. 如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.
(1)、求出y1、y2与工龄x之间的函数关系式;(2)、现年28岁的高级技工小张从18岁起一直在深圳实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)、已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?35. 在平面直角坐标系xOy中,抛物线G: 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数 ( )的图像为直线 .(1)、求A、B两点的坐标;(2)、当1≤x≤2时, ≤ ≤ ,试说明:抛物线G的顶点不在直线 上;(3)、设 ,直线 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.36. 如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.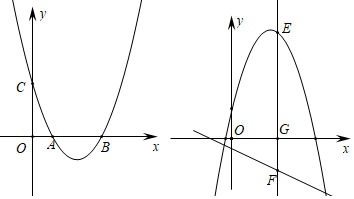 (1)、求抛物线的表达式和顶点D的坐标;(2)、在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;(3)、将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=- x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.37. 在平面直角坐标系 中,点 、 的横坐标分别为 、 ,二次函数 的图像经过点 、 ,且 满足 ( 为常数).
(1)、求抛物线的表达式和顶点D的坐标;(2)、在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;(3)、将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=- x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.37. 在平面直角坐标系 中,点 、 的横坐标分别为 、 ,二次函数 的图像经过点 、 ,且 满足 ( 为常数).
(1)、若一次函数 的图像经过 、 两点.①当 、 时,求 的值;
②若 随 的增大而减小,求 的取值范围.
(2)、当 且 、 时,判断直线 与 轴的位置关系,并说明理由;(3)、点 、 的位置随着 的变化而变化,设点 、 运动的路线与 轴分别相交于点 、 ,线段 的长度会发生变化吗?如果不变,求出 的长;如果变化,请说明理由.
38. 已知抛物线y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)与x轴分别交于A(x1 , 0)、B(x2 , 0)两点,直线y2=2x+t经过点A.
 (1)、已知A、B两点的横坐标分别为3、﹣1.
(1)、已知A、B两点的横坐标分别为3、﹣1.①当a=1时,直接写出抛物线y1和直线y2相应的函数表达式;
②如图,已知抛物线y1在3<x<4这一段位于直线y2的下方,在5<x<6这一段位于直线y2的上方,求a的取值范围;
(2)、若函数y=y1+y2的图象与x轴仅有一个公共点,探求x2﹣x1与a之间的数量关系.
39. 如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.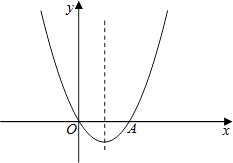 (1)、常数m= , 点A的坐标为;(2)、若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;(3)、若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.40. 已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.(1)、求该抛物线的解析式及顶点D的坐标;(2)、若点P(0,t)是y轴上的一个动点,请进行如下探究:
(1)、常数m= , 点A的坐标为;(2)、若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;(3)、若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.40. 已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.(1)、求该抛物线的解析式及顶点D的坐标;(2)、若点P(0,t)是y轴上的一个动点,请进行如下探究:探究一:如图1,设△PAD的面积为S,令W=t•S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
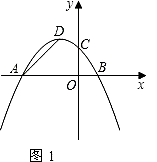
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= )