苏科版备考2021年中考数学三轮冲刺专题7 锐角三角函数
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
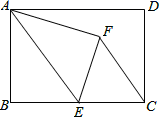
1. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE 沿AE折叠,点B落在点F处,连接FC,则tan∠ECF = ( )
 A、
A、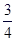 B、
B、 C、
C、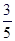 D、
D、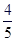 2. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
2. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.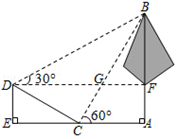 A、10 B、15 C、15 D、15 ﹣53. 斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )A、500sinα米 B、 米 C、500cosα米 D、 米4. 如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )km
A、10 B、15 C、15 D、15 ﹣53. 斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )A、500sinα米 B、 米 C、500cosα米 D、 米4. 如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )km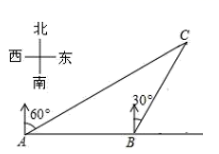 A、 B、 C、 D、5. 一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达 处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A、 B、 C、 D、5. 一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达 处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )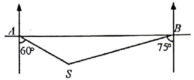 A、 海里、15海里 B、 海里、15海里 C、 海里、 海里 D、 海里、 海里6. 如图,一辆小车沿倾斜角为
A、 海里、15海里 B、 海里、15海里 C、 海里、 海里 D、 海里、 海里6. 如图,一辆小车沿倾斜角为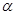 的斜坡向上行驶13米,已知 ,则小车上升的高度是( )
的斜坡向上行驶13米,已知 ,则小车上升的高度是( )  A、5米 B、6米 C、6.5米 D、12米7. 如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )
A、5米 B、6米 C、6.5米 D、12米7. 如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )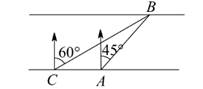 A、60( +1)米 B、30( +1)米 C、(90-30 )米 D、30( -1)米8. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )
A、60( +1)米 B、30( +1)米 C、(90-30 )米 D、30( -1)米8. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )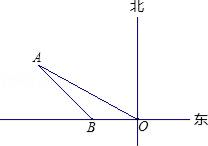 A、 海里 B、 海里 C、 海里 D、 海里9. 如图,一船以每小时36海里的速度向正北航行到A处,发现它的东北方向有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在它的北偏东75°方向,则此时船与灯塔的距离为( )
A、 海里 B、 海里 C、 海里 D、 海里9. 如图,一船以每小时36海里的速度向正北航行到A处,发现它的东北方向有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在它的北偏东75°方向,则此时船与灯塔的距离为( )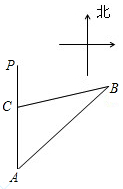 A、24 B、 C、 D、10. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A、24 B、 C、 D、10. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )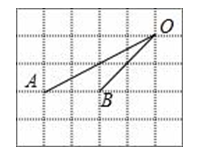 A、 B、 C、 D、11. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A、 B、 C、 D、11. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )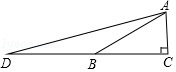 A、 B、 C、 D、12. 如图,小东在同一平面上按照如下步骤进行尺规作图:
A、 B、 C、 D、12. 如图,小东在同一平面上按照如下步骤进行尺规作图:( 1 )作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧交于点C;
( 2 )以C为圆心,以AB长为半径作弧交AC的延长线于点D;
( 3 )连接BD,BC.则下列说法中不正确的是( )
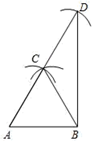 A、∠ABD=90° B、sin2A+cos2D=1 C、DB= AB D、点C是△ABD的外心13. 若锐角三角函数tan55°=a,则a的范围是( )A、0<a<1 B、1<a<2 C、2<a<3 D、3<a<414.
A、∠ABD=90° B、sin2A+cos2D=1 C、DB= AB D、点C是△ABD的外心13. 若锐角三角函数tan55°=a,则a的范围是( )A、0<a<1 B、1<a<2 C、2<a<3 D、3<a<414.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
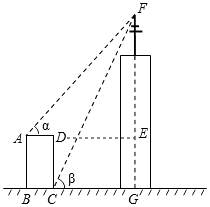 A、(35 +55)m B、(25 +45)m C、(25 +75)m D、(50+20 )m15. 如图,从坡上建筑物AB观测坡底建筑物CD.从A点处测得C点的俯角为45o , 从B点处测得D点的俯角为30o . 已知建筑物AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为( )
A、(35 +55)m B、(25 +45)m C、(25 +75)m D、(50+20 )m15. 如图,从坡上建筑物AB观测坡底建筑物CD.从A点处测得C点的俯角为45o , 从B点处测得D点的俯角为30o . 已知建筑物AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为( )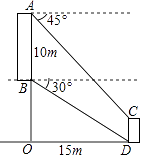 A、(5 ﹣5)m B、(10 ﹣10)m C、(10﹣5 )m D、(10﹣5 )m
A、(5 ﹣5)m B、(10 ﹣10)m C、(10﹣5 )m D、(10﹣5 )m二、填空题
-
16. 如图,小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°.已知办公大楼高46m,CD=10m,则点P到AD的距离为m.(用含根号的式子表示)
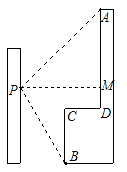 17. 位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间,周边风景秀丽.随着年代的增加,目前塔底低于地面约7米.某校学生先在地面 处侧得塔顶的仰角为30°,再向古塔方向行进 米后到达 处,在 处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么 的值为米.(结果保留根式)
17. 位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间,周边风景秀丽.随着年代的增加,目前塔底低于地面约7米.某校学生先在地面 处侧得塔顶的仰角为30°,再向古塔方向行进 米后到达 处,在 处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么 的值为米.(结果保留根式)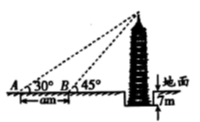 18. 如图,已知点C处有一个高空探测气球,从点C处测得水平地面上A、B两点的俯角分别为30°和45°,若AB=2km,则A、C两点之间的距离为km。
18. 如图,已知点C处有一个高空探测气球,从点C处测得水平地面上A、B两点的俯角分别为30°和45°,若AB=2km,则A、C两点之间的距离为km。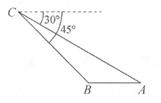 19. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .
19. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .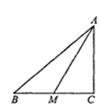 20. 如图,在楼顶点 处观察旗杆 测得旗杆顶部 的仰角为30°,旗杆底部 的俯角为45°.已知楼高 m,则旗杆 的高度为 . (结果保留根号)
20. 如图,在楼顶点 处观察旗杆 测得旗杆顶部 的仰角为30°,旗杆底部 的俯角为45°.已知楼高 m,则旗杆 的高度为 . (结果保留根号)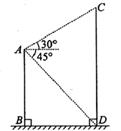 21. 若 为锐角,当 时, .
21. 若 为锐角,当 时, .
22. 在△ABC中,∠C=90°,cosA= ,则tanA等于 .23. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10 米,背水坡CD的坡度i=1: ,则背水坡的坡长CD为米.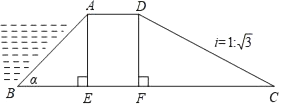 24. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果保留根号).
24. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果保留根号).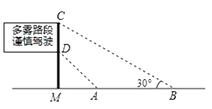 25.
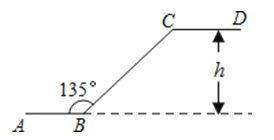
25.如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是6m,则乘电梯从点B到点C上升的高度h是 m.
三、解答题
-
26. 如图,某城市的一座古塔CD坐落在湖边,数学老师带领学生隔湖测量古塔CD的高度,在点A处测得塔尖点D的仰角∠DAC为31°,沿射线AC方向前进35米到达湖边点B处,测得塔尖点D在湖中的倒影E的俯角∠CBE为45°,根据测得的数据,计算这座灯塔的高度CD(结果精确到0.1).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.(结果精确到0.1)
 27. 某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度.他们先在点D用高1.5米的测角仪 测得塔顶M的仰角为30°,然后沿 方向前行 到达点E处,在E处测得塔顶M的仰角为60°.请根据他们的测量数据求此塔 的高.(结果精确 ,参考数据: , , ).
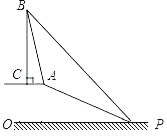
27. 某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度.他们先在点D用高1.5米的测角仪 测得塔顶M的仰角为30°,然后沿 方向前行 到达点E处,在E处测得塔顶M的仰角为60°.请根据他们的测量数据求此塔 的高.(结果精确 ,参考数据: , , ).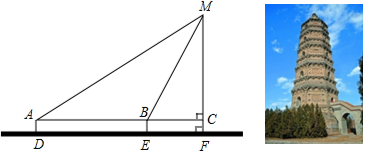 28. 如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点 处测得码头 的船的东北方向,航行40分钟后到达 处,这时码头 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头 的最近距离.(结果精确的0.1海里,参考数据 )
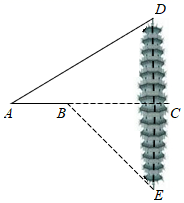
28. 如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点 处测得码头 的船的东北方向,航行40分钟后到达 处,这时码头 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头 的最近距离.(结果精确的0.1海里,参考数据 )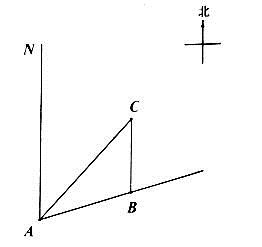 29. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1 m.参考数据:tan34°≈0.67,tan60°= 1.73)
29. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1 m.参考数据:tan34°≈0.67,tan60°= 1.73)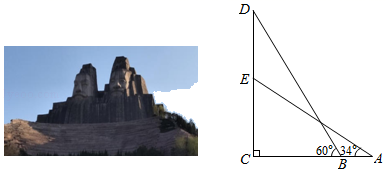 30. 如图,某高楼顶部有一信号发射塔,在矩形建筑物 的 两点测得该塔顶端 的仰角分别为 和 ,矩形建筑物的宽度 ,高度 ,求信号发射塔顶端到地面的距离 . (结果精确到 )
30. 如图,某高楼顶部有一信号发射塔,在矩形建筑物 的 两点测得该塔顶端 的仰角分别为 和 ,矩形建筑物的宽度 ,高度 ,求信号发射塔顶端到地面的距离 . (结果精确到 )(参考数据: )
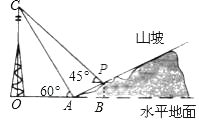
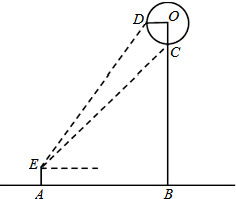
 31. 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
31. 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°=1.192)
 32. 如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
32. 如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)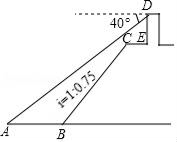 33. 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i= (即tan∠DEM= ),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).
33. 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i= (即tan∠DEM= ),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号). 34. 如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据: ≈1.7,结果保留一位小数)
34. 如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据: ≈1.7,结果保留一位小数)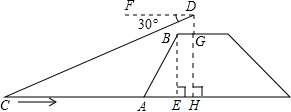 35. 如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70)
35. 如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70) 36. 已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
36. 已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:坡顶A到地面PO的距离;古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
 37. 共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75, ≈1.41
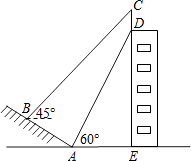
37. 共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75, ≈1.41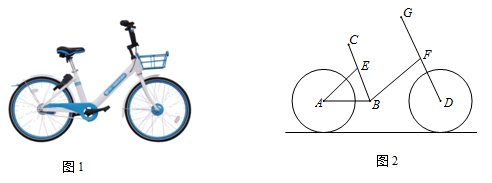 38. 如图,山坡AB的坡度i=1: ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)
38. 如图,山坡AB的坡度i=1: ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)