苏科版备考2021年中考数学三轮冲刺专题6 几何动态及最值问题
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
1. 如图,在边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接CE,将线段CE绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是( )
 A、6 B、3 C、2 D、1.5
A、6 B、3 C、2 D、1.5 -
2. 如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,作AG⊥PQ于点G,则AG的最大值为( )
 A、 B、 C、 D、6
A、 B、 C、 D、6 -
3. 如图,在平面直角坐标系中,已知A(10,0),点P为线段OA上任意一点.在直线y= x上取点E,使PO=PE,延长PE到点F,使PA=PF,分别取OE、AF中点M、N,连结MN,则MN的最小值是( )
 A、4.8 B、5 C、5.4 D、6
A、4.8 B、5 C、5.4 D、6 -
4. 如图,等边△ABC的边长为1,D,E两点分别在边AB,AC上,CE=DE,则线段CE的最小值为( )
 A、2﹣ B、2 ﹣3 C、 D、
A、2﹣ B、2 ﹣3 C、 D、 -
5. 如图,在矩形纸片ABCD中,AB=8,AD=17,折叠纸片使点B落在边AD上的E处,折痕为PQ.当E在AD边上移动时,折痕的端点P,Q也随着移动.若限定P,Q分别在边BA,BC上移动,则点E在边AD上移动的最大距离为( )
 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9 -
6. 如图,正方形 中, ,E,F分别是边 , 上的动点, ,连接 , 交于点P,过点P作 ,且 ,若 的度数最大时,则 长为( )
 A、6 B、 C、 D、
A、6 B、 C、 D、 -
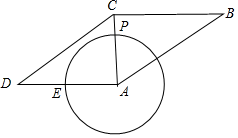
7. 如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作▱ABCD,AB=4 ,⊙A交边AD于点E,当▱ABCD面积为最大值时, 的长为( )
 A、 π B、π C、 π D、3π
A、 π B、π C、 π D、3π -
8. 如图,直线l与⊙O相切于点A,M是⊙O上的一个动点,MH⊥l,垂足为H.若⊙O的半径为1,则MA-MH的最大值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
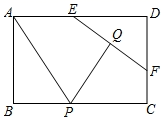
9. 如图,矩形ABCD中,AB=2,AD=3.E,F分别是AD,CD上的动点,EF=2.Q是EF的中点,P为BC上的动点,连接AP,PQ.则AP+PQ的最小值等于( )
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
10. 如图,已知⊙ 的半径为3,圆外一点 满足 ,点 为⊙ 上一动点,经过点 的直线 上有两点 、 ,且OA=OB,∠APB=90°, 不经过点 ,则 的最小值( )
 A、2 B、4 C、5 D、6
A、2 B、4 C、5 D、6 -
11. 如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
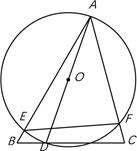 A、 B、 C、2 D、2
A、 B、 C、2 D、2 -
12. 如图,已知A,B两点的坐标分别为(8,0),(0,8),点C,F分别是直线 和 轴上的动点, ,点D是线段 的中点,连接 交 轴于点E,当 面积取得最小值时, 的值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13. 如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )
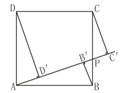 A、1 B、 C、 D、
A、1 B、 C、 D、 -
14. 如图,正方形 中, , 是 中点, 上有一动点 ,连接 、 ,将 沿着 翻折得到 .连接 、 ,则 的最小值为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
15. 如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是 上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为.

-
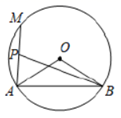
16. 已知点 、 是半径为 的 上两点,且 ,点 是 上一个动点,点 是 的中点,连接 ,则 的最小值是.
-
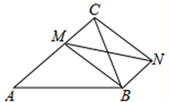
17. 如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是
-
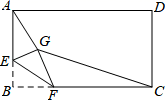
18. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.
-
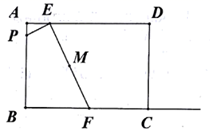
19. 如图,在矩形ABCD中, ,点E在AD边上,且 ,动点P从点A出发,沿AB运动到点B停止,过点E作 ,交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为.
-
20. 如图,折线 中, , ,将折线 绕点A按逆时针方向旋转,得到折线 ,点B的对应点落在线段 上的点D处,点C的对应点落在点E处,连接 ,若 ,则 °.
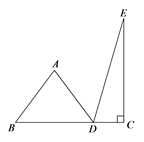
-
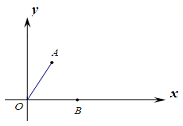
21. 如图,在平面直角坐标系中,A(1, ),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为.
-
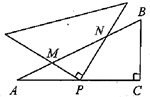
22. 如图,在 中, ,将直角三角板的直角顶点与 边的中点 重合,直角三角板绕着点 旋转,两条直角边分别交 边于 ,则 的最小值是.
-
23. 如图,已知⊙O的半径是2,点A,B在⊙O上,且∠AOB=90°,动点C在⊙O上运动(不与A,B重合),点D为线段BC的中点,连接AD,则线段AD的长度最大值是.

-
24. 如图所示,等边△ABC的边长为4,点D是BC边上一动点,且CE=BD,连接AD,BE,AD与BE相交于点P,连接PC.则线段PC的最小值等于.

-
25. 在Rt△ABC中,∠ABC=90°,AB=8,BC=4.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为.
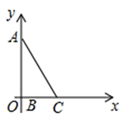
-
26. 如图,正方形ABCD的边长为2,E为BC上一点,且 F为AB边上的一个动点,连接EF,以EF为底向右侧作等腰直角 ,连接CG,则CG的最小值为.

-
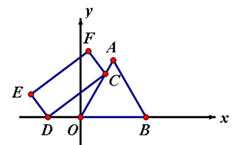
27. 如图,等边△AOB,点C是边AO所在直线上的动点,点D是x轴上的动点,在矩形CDEF中,CD=6,DE= ,则OF的最小值为.
-
28. 如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是.

-
29. 如图,在等边△ABC中,AB=4,点P是BC边上的动点,点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是.

三、综合题
-
30. 如图,在▱ABCD中,AB=5,BC=10,sinB= ,点P以每秒2个单位长度的速度从点B出发,沿着B→C→D→A的方向运动到点A时停止,设点P运动的时间为ts.
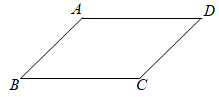 (1)、连接AC,判断△ABC是否是直角三角形,试说明理由;(2)、在点P运动的过程中,若以点C为圆心、PC长为半径的⊙C与AD边相切,求t的值;(3)、在点P出发的同时,点Q以每秒1个单位长度的速度从点C出发,沿着C→D→A的方向运动,当P、Q中的一点到达终点A时,另一点也停止运动.求当BP⊥CQ时t的值.
(1)、连接AC,判断△ABC是否是直角三角形,试说明理由;(2)、在点P运动的过程中,若以点C为圆心、PC长为半径的⊙C与AD边相切,求t的值;(3)、在点P出发的同时,点Q以每秒1个单位长度的速度从点C出发,沿着C→D→A的方向运动,当P、Q中的一点到达终点A时,另一点也停止运动.求当BP⊥CQ时t的值. -
31. 如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,将矩形ABCD沿BE折叠,点A落在点 处,连接 、BD.
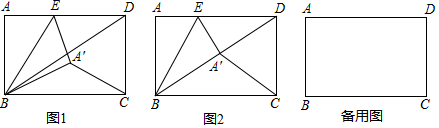 (1)、如图1,求证:∠DE =2∠ABE;(2)、如图2,若点 恰好落在BD上,求tan∠ABE的值;(3)、若AE=2,求 .(4)、点E在AD边上运动的过程中,∠ CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由.
(1)、如图1,求证:∠DE =2∠ABE;(2)、如图2,若点 恰好落在BD上,求tan∠ABE的值;(3)、若AE=2,求 .(4)、点E在AD边上运动的过程中,∠ CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由. -
32. 在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图1,现有矩形纸片ABCD,AB=8cm,AD=6cm.连接BD,将矩形ABCD沿BD剪开,得到△ABD和△BCE.保持△ABD位置不变,将△BCE从图1的位置开始,绕点B按逆时针方向旋转,旋转角为α(0°≤α<360°).在△BCE旋转过程中,边CE与边AB交于点F.

 (1)、如图2,将图1中的△BCE旋转到点C落在边BD上时,CF= ;(2)、继续旋转△BCE,当点E落在DA延长线上时,求出CF的长;(3)、在△BCE旋转过程中,连接AE,AC,当AC=AE时,直接写出此时α的度数及△AEC的面积.
(1)、如图2,将图1中的△BCE旋转到点C落在边BD上时,CF= ;(2)、继续旋转△BCE,当点E落在DA延长线上时,求出CF的长;(3)、在△BCE旋转过程中,连接AE,AC,当AC=AE时,直接写出此时α的度数及△AEC的面积. -
33. 如图, 中, 点E与点B在 的同侧,且 .

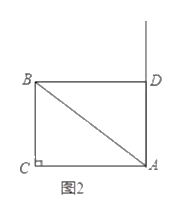 (1)、如图1,点E不与点A重合,连结 交 于点P.设 求y关于x的函数解析式,写出自变量x的取值范围;(2)、是否存在点E,使 与 相似,若存在,求AE的长;若不存在,请说明理由;(3)、如图2,过点 作 垂足为 .将以点 为圆心, 为半径的圆记为 .若点 到 上点的距离的最小值为 ,求 的半径.
(1)、如图1,点E不与点A重合,连结 交 于点P.设 求y关于x的函数解析式,写出自变量x的取值范围;(2)、是否存在点E,使 与 相似,若存在,求AE的长;若不存在,请说明理由;(3)、如图2,过点 作 垂足为 .将以点 为圆心, 为半径的圆记为 .若点 到 上点的距离的最小值为 ,求 的半径. -
34. 如图1,已知:在矩形ABCD中,AB cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以 cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
 (1)、求a的值;(2)、在运动过程中,
(1)、求a的值;(2)、在运动过程中,①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请写出t的值;若不存在,请说明理由.
-
35. 如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.
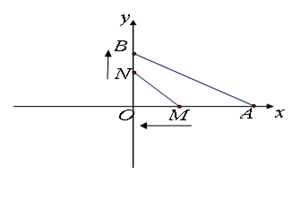
 (1)、若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?(2)、若直线y=x与△OMN外接圆的另一个交点是点C.
(1)、若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?(2)、若直线y=x与△OMN外接圆的另一个交点是点C.①试说明:当0<t<2时,OM、ON、OC在移动过程满足OM+ON= OC;
②试探究:当t>2时,OM、ON、OC之间的数量关系是否发生变化,并说明理由.
-
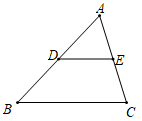
36.(1)、如图,已知△ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE= BC.
 (2)、利用第(1)题的结论,解决下列问题:
(2)、利用第(1)题的结论,解决下列问题:①如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD的中点,求证:EF∥BC,FE= (AD+BC)

②如图,在四边形ABCD中,∠A=90°,AB=3 ,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.

-
37. 如图①,在△ABC中,∠C=90°,AC=15,BC=20,经过点C的⊙O与△ABC的每条边都相交.⊙O与AC边的另一个公共点为D,与BC边的另一个公共点为E,与AB边的两个公共点分别为F、G.设⊙O的半径为r.
 (1)、(操作感知)
(1)、(操作感知)根据题意,仅用圆规在图①中作出一个满足条件的⊙O,并标明相关字母;
(2)、(初步探究)求证:CD2+CE2=4r2;
(3)、当r=8时,则CD2+CE2+FG2的最大值为;(4)、(深入研究)直接写出满足题意的r的取值范围;对于范围内每一个确定的r的值,CD2+CE2+FG2都有最大值,每一个最大值对应的圆心O所形成的路径长为.
-
38. (操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:

第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于 ;
所以图中 即为所求的点.(1)在图②中,连接 ,说明∠ =30°
(方法迁移)
(1)、如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).(2)、已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为.(3)、已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为. -
39.(1)、如图1,点 在 上,请在图中用直尺(不含刻度)和圆规作等边三角形 ,使得点B、C都在 上.
 (2)、已知矩形 中, , .
(2)、已知矩形 中, , .①如图2,当 时,请在图中用直尺(不含刻度)和圆规作等边三角形 ,使得点 在边 上,点 在边 上;

②若在该矩形中总能作出符合①中要求的等边三角形 ,请直接写出 的取值范围.
-
40. (概念认识)
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
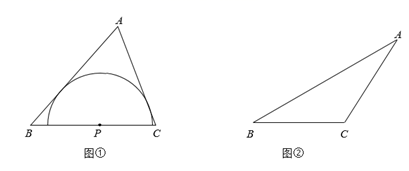 (1)、(初步思考)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为.(2)、如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).(3)、(深入研究)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
(1)、(初步思考)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为.(2)、如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).(3)、(深入研究)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.