苏科版备考2021年中考数学三轮冲刺专题5 图形的变换
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
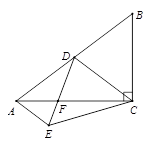
1. 已知Rt△ACB中,点D为斜边AB的中点,连接CD,将△DCB沿直线DC翻折,使点B落在点E的位置,连接DE、CE、AE,DE交AC于点F,若BC=6,AC=8,则AE的值为( )
 A、 B、 C、 D、2. 点A (4,3)经过某种图形变化后得到点B(-3,4),这种图形变化可以是( )A、关于x轴对称 B、关于y轴对称 C、绕原点逆时针旋转90° D、绕原点顺时针旋转90°3. 如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )
A、 B、 C、 D、2. 点A (4,3)经过某种图形变化后得到点B(-3,4),这种图形变化可以是( )A、关于x轴对称 B、关于y轴对称 C、绕原点逆时针旋转90° D、绕原点顺时针旋转90°3. 如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )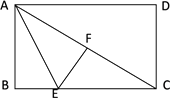 A、 B、6 C、4 D、54.
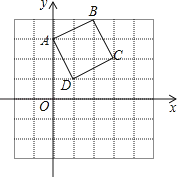
A、 B、6 C、4 D、54.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
 A、(﹣2,2) B、(4,1) C、(3,1) D、(4,0)5. 若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6.
A、(﹣2,2) B、(4,1) C、(3,1) D、(4,0)5. 若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6.如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
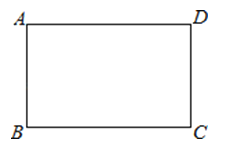 A、2条 B、4条 C、8条 D、无数条7.
A、2条 B、4条 C、8条 D、无数条7.如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是( )
 A、① B、② C、③ D、④8.
A、① B、② C、③ D、④8.△ABC在如图所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得△A1B1C1 , 再将△A1B1C1绕点O旋转180°后得到△A2B2C2 . 则下列说法正确的是( )
 A、A1的坐标为(3,1) B、S四边形ABB1A1=3 C、B2C=2 D、∠AC2O=45°9.
A、A1的坐标为(3,1) B、S四边形ABB1A1=3 C、B2C=2 D、∠AC2O=45°9.图a是矩形纸片,∠SAB=20°,将纸片沿AB折叠成图b,再沿BN折叠成图c,则图c中的∠TBA的度数是( )
 A、120° B、140° C、150° D、160°10.
A、120° B、140° C、150° D、160°10.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,则下列结论正确的是( )
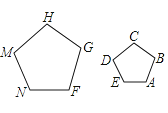 A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F11.
A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F11.如图,图2的图案是由图1中五种基本图形中的两种拼接而成,这两种基本图形是( )
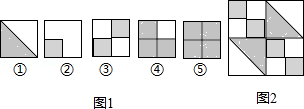 A、①② B、①③ C、①④ D、③⑤12. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )A、
A、①② B、①③ C、①④ D、③⑤12. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )A、 B、
B、 C、
C、 D、
D、 13.
13.一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
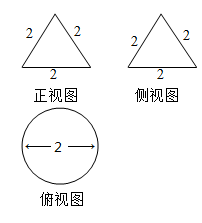 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 如图所示,在平面直角坐标系xOy中,在直线x=1处放置反光镜Ⅰ,在y轴处放置一个需开缺口的挡板Ⅱ,缺口为线段AB,其中点A(0,1),点B在点A上方,在直线x=﹣2处放置一个挡板Ⅲ,从点O发出的光线经反光镜Ⅰ反射后,通过缺口AB照射在挡板Ⅲ上,若需在挡板Ⅲ形成长度为2的光线,则在挡板Ⅱ需开缺口AB的长度为.
 15. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.则CG=.
15. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.则CG=.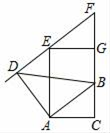 16. 如图,在 中, , ,点 是边 上一点(点 不与点 , 重合),将 沿 翻折,点 的对应点是 , 交 于点 ,若 ,则 的长为.
16. 如图,在 中, , ,点 是边 上一点(点 不与点 , 重合),将 沿 翻折,点 的对应点是 , 交 于点 ,若 ,则 的长为.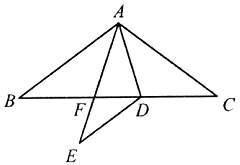 17. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,BE的长为 .
17. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,BE的长为 .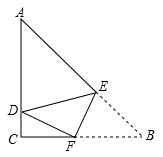 18. 如图,把△ABC沿着BC的方向平移1个单位得到△DEF,重叠部分的面积是△ABC面积的 ,则BC= .
18. 如图,把△ABC沿着BC的方向平移1个单位得到△DEF,重叠部分的面积是△ABC面积的 ,则BC= .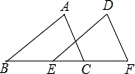 19. 在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为 . (结果用含有a,b,c的式子表示)
19. 在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为 . (结果用含有a,b,c的式子表示)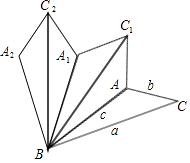 20. 如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 .
20. 如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 .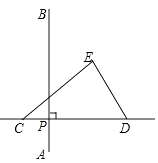 21. 通过平移把点A(2,﹣3)移到点A′(4,﹣2),按同样的平移方式可将点B(﹣3,1)移到点B′,则点B′的坐标是 .
21. 通过平移把点A(2,﹣3)移到点A′(4,﹣2),按同样的平移方式可将点B(﹣3,1)移到点B′,则点B′的坐标是 .
22. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外币A处到达内壁B处的最短距离为 . 23. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 .
23. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 . 24. 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1 , 则图中的阴影部分的面积为 .
24. 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1 , 则图中的阴影部分的面积为 . 25. 若点A(a,3a﹣b)、B(b,2a+b﹣2)关于x轴对称,则a= , b=
25. 若点A(a,3a﹣b)、B(b,2a+b﹣2)关于x轴对称,则a= , b=
26. 平面直角坐标系中的点P(2-m,m)关于x轴的对称点在第四象限,则m的取值范围为
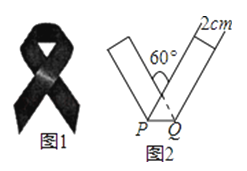
27.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是 .
 28.
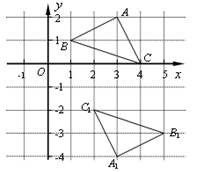
28.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是 .
 29.
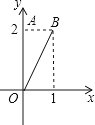
29.如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按逆时针方向旋转90°,则点B的对应点的坐标为 .
 30. 如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1 , 如果点B1 , 落在射线BD上,那么CC1的长度为 .
30. 如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1 , 如果点B1 , 落在射线BD上,那么CC1的长度为 .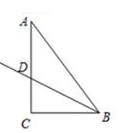 31.
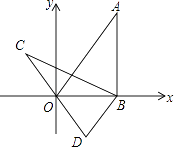
31.如图,在平面直角坐标系xOy中,直线y= x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
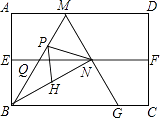
 32. 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
32. 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN=60°;②AM=1;③QN= ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是 .
其中正确结论的序号是 .
三、解答题
-
33.
问题背景:
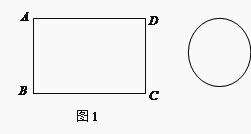
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:
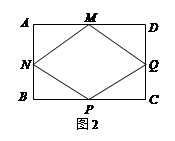
(1)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;
拓展迁移:
(1)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片;
①当BE=DF=时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .34.如图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形,再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的两个矩形为“叠加矩形”.请完成下列问题:
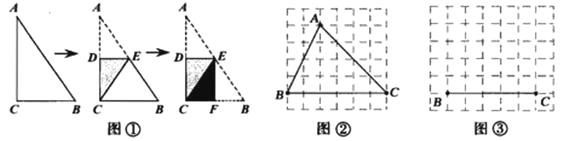
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
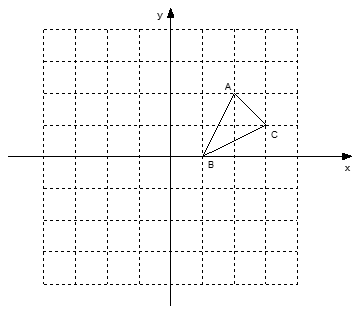
(3)如果一个三角形所折成的“叠加矩形” 为正方形,那么它必须满足的条件是 .35. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1 ,
②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2 ,
③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
 36. 如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
36. 如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?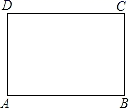
以下是小红的研究过程.
思考过程
要使边AB被三等分,若从边DC上考虑,就是要折出DM= DC,
也就是要折出DM= AB,
当DB、AM相交于F时,即要折出对角线上的DF= DB.那么…
折叠方法和示意图
①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G;
②折出AF、CG,分别交边CD、AB于M、Q;
③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
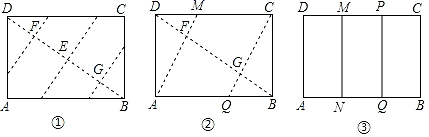 (1)、整理小红的研究过程,说明AN=NQ=QB;(2)、用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)37. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,G是边AB的中点,平行于AB的动直线l分别交△ABC的边CA、CB于点M、N,设CM=m.
(1)、整理小红的研究过程,说明AN=NQ=QB;(2)、用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)37. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,G是边AB的中点,平行于AB的动直线l分别交△ABC的边CA、CB于点M、N,设CM=m.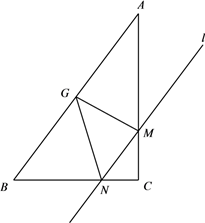 (1)、当m=1时,求△MNG的面积;
(1)、当m=1时,求△MNG的面积;
(2)、若点G关于直线l的对称点为点G′,请求出点G′ 恰好落在△ABC的内部(不含边界)时,m的取值范围;(3)、△MNG是否可能为直角三角形?如果能,请求出所有符合条件的m的值;如果不能,请说明理由.
38. 已知 是一段圆弧上的两点,且在直线 的同侧,分别过这两点作 的垂线,垂足为 是 上一动点,连接 ,且 .(1)、如图①,如果 ,且 ,求 的长;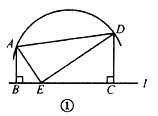
(2)、如图②,若点 恰为这段圆弧的圆心,则线段 之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当 分别在直线 两侧且 ,而其余条件不变时,线段 之间又有怎样的等量关系?请直接写出结论,不必证明.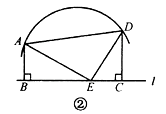 39.
39.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣5,0)、C(﹣1,0),P(a,b)是△ABC的边AC上一点:
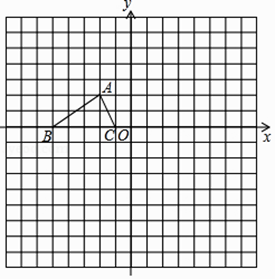 (1)、将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 .(2)、将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().(3)、若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).40. 如图,已知A (﹣4,2),B (﹣2,6),C (0,4)是直角坐标系平面上三点.
(1)、将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 .(2)、将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().(3)、若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).40. 如图,已知A (﹣4,2),B (﹣2,6),C (0,4)是直角坐标系平面上三点. (1)、把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1 , 画出平移后的图形;(2)、若△ABC内部有一点P (a,b),则平移后它的对应点Pl的坐标为;(3)、以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在所给的坐标系中作出所有满足条件的图形.
(1)、把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1 , 画出平移后的图形;(2)、若△ABC内部有一点P (a,b),则平移后它的对应点Pl的坐标为;(3)、以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在所给的坐标系中作出所有满足条件的图形.