苏科版备考2021年中考数学三轮冲刺专题4 圆及其性质
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
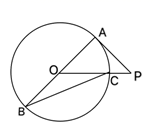
1. 如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=40°,则∠B等于( )
 A、15° B、20° C、25° D、30°2. 如图,AB为⊙O的直径,点C在⊙O上,∠A=24°,则BC弧的度数为( )
A、15° B、20° C、25° D、30°2. 如图,AB为⊙O的直径,点C在⊙O上,∠A=24°,则BC弧的度数为( )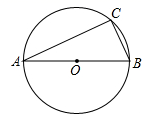 A、66° B、48° C、33° D、24°3. 如图,AB是⊙O的直径,CD是⊙O的弦,连结AC、AD、BD,若∠BAC=35°,则∠ADC 的度数为
A、66° B、48° C、33° D、24°3. 如图,AB是⊙O的直径,CD是⊙O的弦,连结AC、AD、BD,若∠BAC=35°,则∠ADC 的度数为 A、35° B、55° C、65° D、70°4. 如图,AB是⊙O的直径,O是圆心,弦CD⊥AB于E,AB=10,CD=8,则OE的长为( )
A、35° B、55° C、65° D、70°4. 如图,AB是⊙O的直径,O是圆心,弦CD⊥AB于E,AB=10,CD=8,则OE的长为( )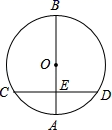 A、2 B、3 C、4 D、55. 如图,点 在 上, , ,则 等于( )
A、2 B、3 C、4 D、55. 如图,点 在 上, , ,则 等于( )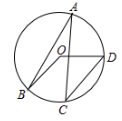 A、 B、 C、 D、6. 如图,AB是☉O的直径,点C在AB的延长线上,CD切☉O于点D,若∠A=25°,则∠C的度数是( )
A、 B、 C、 D、6. 如图,AB是☉O的直径,点C在AB的延长线上,CD切☉O于点D,若∠A=25°,则∠C的度数是( )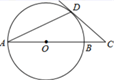 A、40º B、50º C、55º D、65º7. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
A、40º B、50º C、55º D、65º7. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )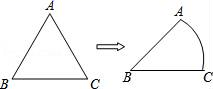 A、( )° B、( )° C、( )° D、( )°8. 如图,从⊙O外一点 A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=32°,则∠ACB的度数是( )
A、( )° B、( )° C、( )° D、( )°8. 如图,从⊙O外一点 A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=32°,则∠ACB的度数是( ) A、29° B、30° C、31° D、32°9. 已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )A、24π B、36π C、70π D、72π10. 如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为( )
A、29° B、30° C、31° D、32°9. 已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )A、24π B、36π C、70π D、72π10. 如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为( ) A、30° B、40° C、50° D、60°11. 如图,已知C为 上一点,若∠AOB=100°,则∠ACB的度数为( )
A、30° B、40° C、50° D、60°11. 如图,已知C为 上一点,若∠AOB=100°,则∠ACB的度数为( ) A、50° B、80° C、100° D、130°12. 如图,点A,B,C,D都在⊙O上,BD为直径,若∠A=65°,则∠DBC的值是( )
A、50° B、80° C、100° D、130°12. 如图,点A,B,C,D都在⊙O上,BD为直径,若∠A=65°,则∠DBC的值是( )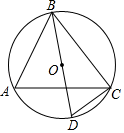 A、65° B、25° C、35° D、15°13. 如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
A、65° B、25° C、35° D、15°13. 如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 如图,在△ABC中,BC=6,以点A为圆心,2为半径的☉A与BC相切于点D,交AB于点E,交AC于点F,点P是优弧 上的一点,且∠EPF=50°,则图中阴影部分的面积是.
 15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r =4,扇形的圆心角θ=120°,则该圆锥母线l的长为.
15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r =4,扇形的圆心角θ=120°,则该圆锥母线l的长为.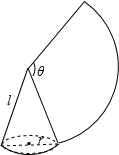 16. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.
16. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.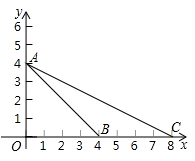 17. 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7 , 则∠A4A1A7=°.
17. 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7 , 则∠A4A1A7=°.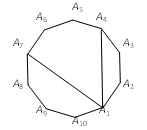 18. 若△ABC的三边长为3、4、5,则△ABC的外接圆半径R与内切圆半径r的差为.19. 如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为°.
18. 若△ABC的三边长为3、4、5,则△ABC的外接圆半径R与内切圆半径r的差为.19. 如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为°. 20. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )
20. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )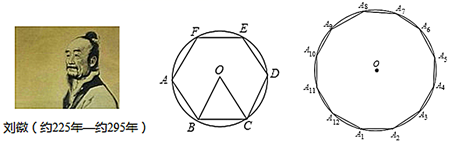 21. P是△ABC的内心,BC=4,∠BAC=90°,则△PBC的外接圆半径为.22. 如图,在△ABC中,AB=AC=5,BC=6,则△ABC的内切圆⊙I与外接圆⊙O的周长之比为。
21. P是△ABC的内心,BC=4,∠BAC=90°,则△PBC的外接圆半径为.22. 如图,在△ABC中,AB=AC=5,BC=6,则△ABC的内切圆⊙I与外接圆⊙O的周长之比为。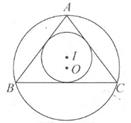 23. 如图,在四边形 中, , , ,以点A为圆心, 为半径的圆与 相切于点E,交 于点F.用扇形 围成一个圆锥的侧面,则这个圆锥底面圆的半径为.
23. 如图,在四边形 中, , , ,以点A为圆心, 为半径的圆与 相切于点E,交 于点F.用扇形 围成一个圆锥的侧面,则这个圆锥底面圆的半径为.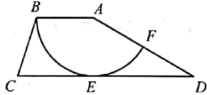 24. 如图,AD是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AD的延长线于点B.若∠A=32°,则∠B=°.
24. 如图,AD是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AD的延长线于点B.若∠A=32°,则∠B=°. 25. T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b= ;③a:b=1: ;④S1:S2=3:4.其中正确的有.(填序号)
25. T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b= ;③a:b=1: ;④S1:S2=3:4.其中正确的有.(填序号)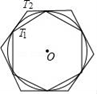 26. 如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 。
26. 如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 。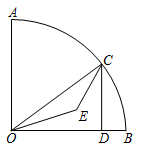
三、解答题
-
27.
如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
 (1)、直接写出ED和EC的数量关系: ;(2)、DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;(3)、填空:当BC= 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .28.
(1)、直接写出ED和EC的数量关系: ;(2)、DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;(3)、填空:当BC= 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .28.如图,点C在以AB为直径的⊙O上,∠CAB=30°,点D在AB上由点B开始向点A运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.
(1)求证:CE=CF;
(2)如果CD⊥AB,求证:EF为⊙O的切线.
 29. 用两种方法证明“圆的内接四边形对角互补”.
29. 用两种方法证明“圆的内接四边形对角互补”.已知:如图①,四边形ABCD内接于⊙O.
求证:∠B+∠D=180°.


证法1:如图②,作直径DE交⊙O于点E,连接AE、CE.
∵DE是⊙O的直径,
∴( ).
∵∠DAE+∠AEC+∠DCE+∠ADC=360°,
∴∠AEC+∠ADC=360°-∠DAE-∠DCE=360°-90°-90°=180°.
∵∠B和∠AEC所对的弧是 ,
∴( ).
∴∠B+∠ADC=180°.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
30. 如图,AB为⊙O直径,C为⊙O上一点,点D是 的中点,DE⊥AC于E,DF⊥AB于F.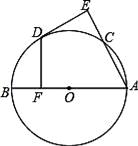 (1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.31. 如图,过点A的直线DE和正三角形ABC的边BC平行.
(1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.31. 如图,过点A的直线DE和正三角形ABC的边BC平行.
( 1 )利用直尺和圆规作△ABC的外接圆O(不写作法,保留作图痕迹);
( 2 )求证:DE是⊙O的切线.
32. 如图,四边形ABCD内接于⊙O,已知AB=AC,延长CD至点E,使CE=BD,连结AE.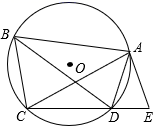 (1)、求证:AD平分∠BDE;(2)、若AB∥CD,求证:AE是⊙O的切线.33. 如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)、求证:AD平分∠BDE;(2)、若AB∥CD,求证:AE是⊙O的切线.33. 如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC. (1)、试判断BC与⊙O的位置关系,并说明理由;(2)、若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).34. 如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)、试判断BC与⊙O的位置关系,并说明理由;(2)、若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).34. 如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.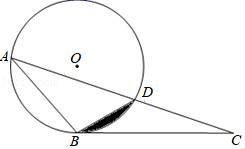 (1)、证明BC与⊙O相切;(2)、若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.35. 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)、证明BC与⊙O相切;(2)、若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.35. 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE. (1)、求证:AE是⊙O的切线;(2)、已知AE=8cm,CD=12cm,求⊙O的半径.36. 如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是 上一点.
(1)、求证:AE是⊙O的切线;(2)、已知AE=8cm,CD=12cm,求⊙O的半径.36. 如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是 上一点. (1)、若AC为⊙O的切线,试说明:∠AED=∠CAD;(2)、若AE平分∠BAD,延长DE、AB交于点P,若PB=BO,DE=2,求PD的长.37. 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)、若AC为⊙O的切线,试说明:∠AED=∠CAD;(2)、若AE平分∠BAD,延长DE、AB交于点P,若PB=BO,DE=2,求PD的长.37. 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. (1)、求证:EF⊥AB;(2)、若∠C=30°,EF= ,求EB的长.38. 如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
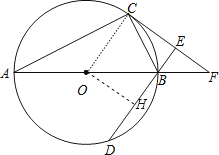
(1)、求证:EF⊥AB;(2)、若∠C=30°,EF= ,求EB的长.38. 如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO. (1)、求证:PB为⊙O的切线;
(1)、求证:PB为⊙O的切线;
(2)、若⊙O的半径为1,PA=3,求BC的长.