苏科版备考2021年中考数学三轮冲刺专题3 基本角形性质
试卷更新日期:2021-05-26 类型:三轮冲刺
一、单选题
-
1.
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货箱的三视图画了出来,如图.请你根据三视图帮他清点出箱子的个数是( )
 A、6 B、7 C、8 D、92.
A、6 B、7 C、8 D、92.如图所示的平面图形能折叠成的长方体是( )
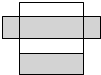 A、
A、 B、
B、 C、
C、 D、
D、 3. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( )
3. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( ) A、点O1 B、点O2 C、点O3 D、点O44. 若多边形的边数增加一条,则它的外角和( )A、增加180° B、不变 C、增加360° D、减少180°5. 下列图形中,是中心对称图形的是( )
A、点O1 B、点O2 C、点O3 D、点O44. 若多边形的边数增加一条,则它的外角和( )A、增加180° B、不变 C、增加360° D、减少180°5. 下列图形中,是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 6. 如图,△ABC是等边三角形,点C在直线b上,若直线a∥b,∠1=34°,则∠2的度数为( )
6. 如图,△ABC是等边三角形,点C在直线b上,若直线a∥b,∠1=34°,则∠2的度数为( ) A、26° B、28° C、34° D、36°7. 若一个三角形的两边长分别为4和6,则第三边长可能是( )A、12 B、10 C、8 D、28. 如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )
A、26° B、28° C、34° D、36°7. 若一个三角形的两边长分别为4和6,则第三边长可能是( )A、12 B、10 C、8 D、28. 如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )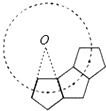 A、10 B、9 C、8 D、79. 下列命题中,是真命题的为( )A、四个角相等的四边形是矩形 B、四边相等的四边形是正方形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形10. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列符合题意的是( )
A、10 B、9 C、8 D、79. 下列命题中,是真命题的为( )A、四个角相等的四边形是矩形 B、四边相等的四边形是正方形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形10. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列符合题意的是( )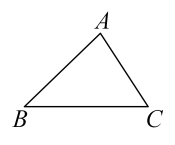 A、
A、 B、
B、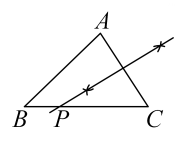 C、
C、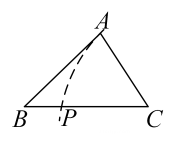 D、
D、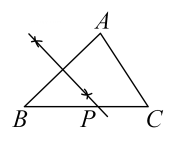 11. 如图,在 中, 是 的中点,将 沿 翻折得到 ,连接 ,则线段 的长等于( )
11. 如图,在 中, 是 的中点,将 沿 翻折得到 ,连接 ,则线段 的长等于( ) A、2 B、 C、 D、12. 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
A、2 B、 C、 D、12. 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )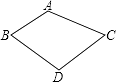 A、90° B、110° C、120° D、140°13. 如图,点E在正方形ABCD的边BC上,将△ABE沿直线AE折叠,使点B落在正方形内点P处,延长EP交CD于点F,连接AF.若点E在BC上移动,则下列结论正确的是( )
A、90° B、110° C、120° D、140°13. 如图,点E在正方形ABCD的边BC上,将△ABE沿直线AE折叠,使点B落在正方形内点P处,延长EP交CD于点F,连接AF.若点E在BC上移动,则下列结论正确的是( ) A、△AEF的周长不变 B、△AEF的面积不变 C、△CEF的周长不变 D、△CEF的面积不变
A、△AEF的周长不变 B、△AEF的面积不变 C、△CEF的周长不变 D、△CEF的面积不变二、填空题
-
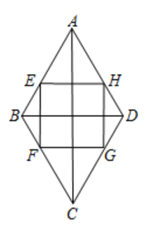
14. 如图,四边形EFGH是菱形ABCD内接正方形,若 ,若正方形的边长为2,则AC + BD =.
 15. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
15. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论: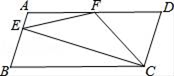 (1)、∠DCF+ ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.其中一定成立的是(把所有正确结论的序号都填在横线上)16. 如图,把 绕点 顺时针方旋转36°得到 ,若 正好经过 点,则 =°
(1)、∠DCF+ ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.其中一定成立的是(把所有正确结论的序号都填在横线上)16. 如图,把 绕点 顺时针方旋转36°得到 ,若 正好经过 点,则 =° 17. 如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=.(用含α的代数式表示)
17. 如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=.(用含α的代数式表示) 18. 一个矩形的周长为16,面积为14,则该矩形的对角线长为 .
18. 一个矩形的周长为16,面积为14,则该矩形的对角线长为 .
19. 《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC=尺.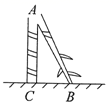 20. 如图,将等腰直角三角形ABC(∠B=90°)沿EF折叠,使点A落在BC边的中点A1处,BC=8,那么线段AE的长度为.
20. 如图,将等腰直角三角形ABC(∠B=90°)沿EF折叠,使点A落在BC边的中点A1处,BC=8,那么线段AE的长度为.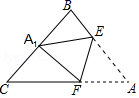 21. 如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是.
21. 如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是. 22. 如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为 .
22. 如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为 .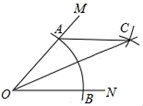 23. 如图,点B、E、C、F在一条直线上, AC∥DF,且AC=DF,请添加一个条件 , 使△ABC≌△DEF.
23. 如图,点B、E、C、F在一条直线上, AC∥DF,且AC=DF,请添加一个条件 , 使△ABC≌△DEF. 24. 如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.
24. 如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.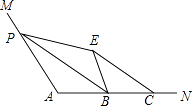 25. 若一个正多边形的外角与它的内角相等,则这个多边形为.26. 命题:“如果a = b ,那么a2=b2”的逆命题是命题(填“真”或“假”)27. 如图,点O是正五边形ABCDE的中心,连接BD、OD,则∠BDO=°.
25. 若一个正多边形的外角与它的内角相等,则这个多边形为.26. 命题:“如果a = b ,那么a2=b2”的逆命题是命题(填“真”或“假”)27. 如图,点O是正五边形ABCDE的中心,连接BD、OD,则∠BDO=°. 28.
28.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
 29. 将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= .
29. 将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= . 30. 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为 .
30. 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为 .
三、解答题
-
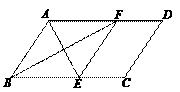
31. 如图,在▱ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,连接EF.
求证:四边形ABEF是菱形.
 32. 已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
32. 已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. (1)、求证:△AOD ≌ △EOC;(2)、连接AC,DE,当∠B ∠AEB 等于多少度时,四边形ACED是正方形?请说明理由.
(1)、求证:△AOD ≌ △EOC;(2)、连接AC,DE,当∠B ∠AEB 等于多少度时,四边形ACED是正方形?请说明理由. 33. 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
33. 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. (1)、已知BD= ,求正方形ABCD的边长;(2)、猜想线段CM与CN的数量关系并加以证明.34. 如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
(1)、已知BD= ,求正方形ABCD的边长;(2)、猜想线段CM与CN的数量关系并加以证明.34. 如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
 35. 按要求作图,不要求写做法,但要保留作图痕迹.
35. 按要求作图,不要求写做法,但要保留作图痕迹. (1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.(2)、如图2,点E是菱形ABCD的对角线BD上一点,请只用直尺(不带刻度)作菱形AECF.36.
(1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.(2)、如图2,点E是菱形ABCD的对角线BD上一点,请只用直尺(不带刻度)作菱形AECF.36.如图所示,在7×6的正方形网格中,选取14个格点,以其中三个格点为顶点画出ABC,请你以选取的格点为顶点再画出一个三角形,且分别满足下列条件:
(1)图①中所画的三角形与ABC组成的图形是轴对称图形;
(2)图②中所画的三角形与ABC组成的图形是中心对称图形.
 37. 如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
37. 如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.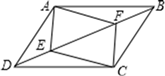
求证:
(1)、AE=CF;(2)、四边形AECF是平行四边形.38. 如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.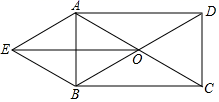 (1)、求证:四边形AOBE是菱形;(2)、若∠EAO+∠DCO=180°,DC=3,求四边形ADOE的面积.39. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
(1)、求证:四边形AOBE是菱形;(2)、若∠EAO+∠DCO=180°,DC=3,求四边形ADOE的面积.39. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,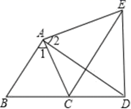 (1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.40. 如图,在由边长为1的小正方形组成的网格图中,有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形.)
(1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.40. 如图,在由边长为1的小正方形组成的网格图中,有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形.)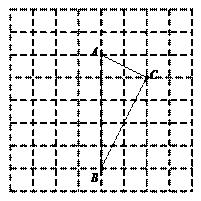 (1)、△ABC是三角形(填“锐角”、“直角”或“钝角”);(2)、若P、Q分别为线段AB、BC上的动点,当PC+PQ取得最小值时,
(1)、△ABC是三角形(填“锐角”、“直角”或“钝角”);(2)、若P、Q分别为线段AB、BC上的动点,当PC+PQ取得最小值时,① 在网格中用无刻度的直尺,画出线段PC、PQ.(请保留作图痕迹.)
② 直接写出PC+PQ的最小值:.