重庆市大渡口区2021九年级指标到校数学试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 下列四个数中,是负数的是( )A、1 B、2 C、3 D、-42. 下列四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2021年2月10日19时52分,中国首次火星探测任务“天问一号”成功“刹车”被火星“捕获”.在制动捕获过程中,火星环绕器面临着诸多困难,比如探测器距离地球约 公里,无法实时监控.其中数据 用科学记数法表示为( )A、 B、 C、 D、4. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个正三角形,第(2)个图案有7个正三角形,第(3)个图案有10个正三角形,…依此规律.第 个图案有22个三角形,则 ( )
3. 2021年2月10日19时52分,中国首次火星探测任务“天问一号”成功“刹车”被火星“捕获”.在制动捕获过程中,火星环绕器面临着诸多困难,比如探测器距离地球约 公里,无法实时监控.其中数据 用科学记数法表示为( )A、 B、 C、 D、4. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个正三角形,第(2)个图案有7个正三角形,第(3)个图案有10个正三角形,…依此规律.第 个图案有22个三角形,则 ( ) A、6 B、7 C、8 D、95. 如图,一个油桶靠在直立的墙边,量得 并且 则这个油桶的底面半径是( )
A、6 B、7 C、8 D、95. 如图,一个油桶靠在直立的墙边,量得 并且 则这个油桶的底面半径是( ) A、 B、 C、 D、6. 已知 则 的值为( )A、-2 B、-4 C、4 D、67. 若使算式 的运算结果最小,则 表示的运算符号是( )A、 B、 C、 D、8. 如图,线段CD两个端点的坐标分别为 , ,以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为 ,则点A的坐标为
A、 B、 C、 D、6. 已知 则 的值为( )A、-2 B、-4 C、4 D、67. 若使算式 的运算结果最小,则 表示的运算符号是( )A、 B、 C、 D、8. 如图,线段CD两个端点的坐标分别为 , ,以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为 ,则点A的坐标为 A、 B、 C、 D、9. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 是平行于水平地面 的一个平台、小华想利用所学知识测量古塔的高度 ,她在平台的点 处水平放置一平面镜, 她沿着 方向移动,当移动到点 时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知,根据题中提供的相关信息,古塔的高度 约为(参考数据: )( )
A、 B、 C、 D、9. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 是平行于水平地面 的一个平台、小华想利用所学知识测量古塔的高度 ,她在平台的点 处水平放置一平面镜, 她沿着 方向移动,当移动到点 时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知,根据题中提供的相关信息,古塔的高度 约为(参考数据: )( )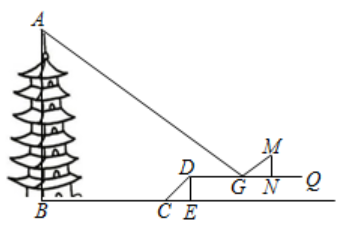 A、19.5 B、19.7 C、21.3 D、22.110. 如果关于 的分式方程 有非负整数解,关于 的不等式组 有且只有三个整数解,则所有符合条件的整数 的个数为( )A、0 B、1 C、2 D、311. 如图,已知正方形 的边长为4,将正方形 沿 对折,使点 恰好落在边 的中点 处,点 的对应点为点 延长 交 的延长线于 ,连接对角线 交折痕 于Q,则线段 的长为( )
A、19.5 B、19.7 C、21.3 D、22.110. 如果关于 的分式方程 有非负整数解,关于 的不等式组 有且只有三个整数解,则所有符合条件的整数 的个数为( )A、0 B、1 C、2 D、311. 如图,已知正方形 的边长为4,将正方形 沿 对折,使点 恰好落在边 的中点 处,点 的对应点为点 延长 交 的延长线于 ,连接对角线 交折痕 于Q,则线段 的长为( ) A、 B、 C、 D、12. 如图,平行四边形 的顶点 在 轴正半轴上, 平行于 轴,直线 交 轴于点 ,连接 ,反比例函数 的图象经过点 已知 ,则 的值是( )
A、 B、 C、 D、12. 如图,平行四边形 的顶点 在 轴正半轴上, 平行于 轴,直线 交 轴于点 ,连接 ,反比例函数 的图象经过点 已知 ,则 的值是( )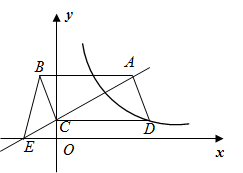 A、 B、 C、 D、5
A、 B、 C、 D、5二、填空题
-
13. .14. 已知一个多边形的每个外角都等于 则它的边数是.15. 在网络课程学习中,韩梅和李雷分别在《数学与天文》、《数学与绘画》、《数学与游戏》中随机选择一门,两人恰好选中同一门课程的概率为.16. 如图,在正方形 的边长为 以 为圆心,4为半径作圆弧.以 为圆心,6为半径作圆弧.若图中阴影部分的面积分别为 时,则 .(结果保留 )
 17. 甲、乙两车分别从 地、 地同时向 地匀速行驶 在 两地之间).甲追上乙之后,乙立即以原来速度的2倍向 地继续行驶,且此刻速度大于甲的速度,到达 地后立即以提高后的速度返回 地,甲车到达 地后立即以原来速度返回 地,两车距 地的距离之和 (千米)与甲车行驶的时间 小时)之间的部分函数关系如图所示,那么甲、乙两车第二次相遇时甲行驶的时间是小时.
17. 甲、乙两车分别从 地、 地同时向 地匀速行驶 在 两地之间).甲追上乙之后,乙立即以原来速度的2倍向 地继续行驶,且此刻速度大于甲的速度,到达 地后立即以提高后的速度返回 地,甲车到达 地后立即以原来速度返回 地,两车距 地的距离之和 (千米)与甲车行驶的时间 小时)之间的部分函数关系如图所示,那么甲、乙两车第二次相遇时甲行驶的时间是小时. 18. 如图,矩形 中, ,点 为边 上一动点(不与 重合)、以 为边向外作矩形 ,且 ,连接 点 是线段BF的中点.连接 ,则 的最小值为.
18. 如图,矩形 中, ,点 为边 上一动点(不与 重合)、以 为边向外作矩形 ,且 ,连接 点 是线段BF的中点.连接 ,则 的最小值为.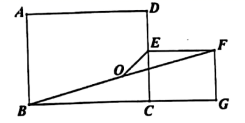
三、解答题
-
19. 计算:(1)、(2)、20. 如图,菱形 中, 交 于点 .
 (1)、尺规作图:过点 作 的垂线,交 于 .(不写作法,保留作图痕迹,并标明字母)(2)、判断线段 和 的数量关系,并证明.21. 为了推动我区教育教学发展,加快教师的成长,在某次研讨课活动中,为了分析某节复习课的教学效果,课前,陈老师让1801班每位同学做6道类似题目(与这节课内容相关),解题情况如图所示:课后,再让学生做6道类似的题目.结果如表所示.已知每位学生至少答对1题.
(1)、尺规作图:过点 作 的垂线,交 于 .(不写作法,保留作图痕迹,并标明字母)(2)、判断线段 和 的数量关系,并证明.21. 为了推动我区教育教学发展,加快教师的成长,在某次研讨课活动中,为了分析某节复习课的教学效果,课前,陈老师让1801班每位同学做6道类似题目(与这节课内容相关),解题情况如图所示:课后,再让学生做6道类似的题目.结果如表所示.已知每位学生至少答对1题.
课后解题情况统计表
答对题数
频数(人)
1
2
2
3
3
3
4
a
5
9
6
13
合计
b
(1)、根据图表信息填空:a=;b= .(2)、该班课前解题时答对题数的众数是;课后答对题数的中位数是 .(3)、请选择适当的统计量,从两个不同的角度评价这节复习课的教学效果.22. 阅读下列材料解决问题:材料一:完全平方数是指可以写成某个整数的平方的数,即其平方根为整数的数.例如, 是一个完全平方数.
材料二:对一个四位数,我们可以记为 ,即 ,若一个四位数的千位数字与百位数字相同,十位与个位数字相同,记为 ,我们称之为和谐四位数.
(1)、已知 是使 成为完全平方数的最小正整数,则 ;(2)、试证明任意一个和谐四位数都是 的倍数;(3)、若有和谐四位数 是一个完全平方数,请求出符合条件的数.23. 在初中阶段的函数学习中,我们经历了“确定函数的表达式一画出函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.在画函数图象时,我们通过列表、描点、连线或平移的方法画出了所学的函数图象.以下是我们研究函数 的图象、性质及其应用的部分过程,请你按要求完成下列问题.(1)、列表:函数自变量 的取值范围是 ,下表列出部分 的对应值:-5
-4
-3
-2
-1
0
1
2
3
2
3
4
1
3
根据表格中的数据计算出: , , , ;
(2)、描点、连线:在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质: ▲ ;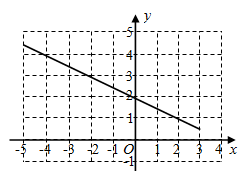 (3)、已知函数 的图象如图所示,直接写出不等式 的解集为;(结果保留位 小数,误差不超过0.1)24. 某小微企业在网上销售 两种品牌木制休闲用品.今年2月,一共销售 两种品牌木制休闲用品共450件,其中 品牌木制休闲用品每件售价20元, 品牌木制休闲用品每件售价30元,2月全部售完这些木制休闲用品,所得总销售额不低于11500元.(1)、 品牌木制休闲用品最多销售多少件?(2)、为了促进销量,今年3月,该店开展了优惠活动, 品牌木制休闲用品的售价比2月的价格优惠 , 品牌木制休闲用品的售价比2月的价格优惠 ,结果3月售出的 品牌木制休闲用品数量比2月总销售额最低时售出的 品牌木制休闲用品数量增加了 ,售出的 品牌木制休闲用品数量比2月总销售额最低时售出的 品牌木制休闲用品数量增加了 ,结果3的总销售额比2月最低销售额增加了 ,求 的值.25. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(3)、已知函数 的图象如图所示,直接写出不等式 的解集为;(结果保留位 小数,误差不超过0.1)24. 某小微企业在网上销售 两种品牌木制休闲用品.今年2月,一共销售 两种品牌木制休闲用品共450件,其中 品牌木制休闲用品每件售价20元, 品牌木制休闲用品每件售价30元,2月全部售完这些木制休闲用品,所得总销售额不低于11500元.(1)、 品牌木制休闲用品最多销售多少件?(2)、为了促进销量,今年3月,该店开展了优惠活动, 品牌木制休闲用品的售价比2月的价格优惠 , 品牌木制休闲用品的售价比2月的价格优惠 ,结果3月售出的 品牌木制休闲用品数量比2月总销售额最低时售出的 品牌木制休闲用品数量增加了 ,售出的 品牌木制休闲用品数量比2月总销售额最低时售出的 品牌木制休闲用品数量增加了 ,结果3的总销售额比2月最低销售额增加了 ,求 的值.25. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C. (1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
(1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
26. 如图,在 中, ,将 绕点 顺时针旋转 得到 ,点 ,点 旋转后的对应分别为点 ,点 (1)、当点 恰好为线段 的中点时, , .(2)、当线段 与 有交点时,记交点为点 .猜想线段 与 的数量关系,画出图形并加以证明;(3)、在满足(2)的条件下,连接 ,请直接写出 长度的取值范围.
(1)、当点 恰好为线段 的中点时, , .(2)、当线段 与 有交点时,记交点为点 .猜想线段 与 的数量关系,画出图形并加以证明;(3)、在满足(2)的条件下,连接 ,请直接写出 长度的取值范围.