浙江省温州市瓯海区2021年数学中考第二次适应性试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数 $\sqrt{2}$ ， $\frac{1}{2}$ ，0，﹣2中，无理数是（）

A、 $\sqrt{2}$ B、 $\frac{1}{2}$ C、0 D、﹣2

查看试题解析
2. 用科学记数法表示2300000，正确的是（）

A、0.23×10⁷ B、2.3×10⁶ C、23×10⁵ D、2.3×10⁷

查看试题解析
3. 某物体如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 在同一副扑克牌中抽取5张“方块”，3张“梅花”，2张“黑桃”．将这10张牌背面朝上，从中任意抽取1张，是“黑桃”的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{3}{10}$ D、 $\frac{1}{5}$

查看试题解析
5. 后疫情时代，小牛电动车销量逆势增长，某店去年6～10月份销量如图所示，相邻的两个月中，月销量增长最快的是（）

A、6月到7月 B、7月到8月 C、8月到9月 D、9月到10月

查看试题解析
6. 如图，四边形ABCD的对角线互相平分，要使它变为菱形，需要添加的条件是（）

A、AB＝CD B、AD＝BC C、AC＝BD D、AB＝BC

查看试题解析
7. 一张小凳子的结构如图所示，AB∥CD ， ∠1＝∠2＝ $α$ ，AD＝50厘米，则小凳子的高度MN为（）

A、50cos $α$ 厘米 B、 $\frac{50}{\cos α}$ 厘米 C、50sin $α$ 厘米 D、 $\frac{50}{\sin α}$ 厘米

查看试题解析
8. 在平面直角坐标系中，过直线l：y＝x＋1上一点A（1，a）作AB⊥x轴于B点，若平移直线l过点B交y轴于C点，则点C的纵坐标为（）

A、﹣ $\frac{2}{3}$ B、﹣ $\frac{3}{2}$ C、﹣1 D、﹣2

查看试题解析
9. 已知二次函数y＝ax²﹣4ax﹣1，当x≤1时，y随x的增大而增大，且﹣1≤x≤6时，y的最小值为﹣4，则a的值为（）

A、1 B、 $\frac{3}{4}$ C、﹣ $\frac{3}{5}$ D、﹣ $\frac{1}{4}$

查看试题解析
10. 如图，在Rt△ABC中，∠ACB＝90°，分别以其三边为边向外作正方形，延长EA交BG于点M ，连接IM交AB于点N ，若M是BG的中点，则 $\frac{B N}{A N}$ 的值为（）

A、 $\frac{2}{15}$ B、 $\frac{1}{8}$ C、 $\frac{\sqrt{5}}{12}$ D、 $\frac{\sqrt{10}}{24}$

查看试题解析

二、填空题

11. 分解因式： $x^{2}$ －9= ．

查看试题解析
12. 对三垟湿地某处鸟类动物进行调查和鉴定后，绘制成如图所示统计图．已知调查发现白鹭数目为15只，那么调查发现燕鸥为只．

查看试题解析
13. 不等式组 ${\begin{array}{l} x - 8 < 0 \\ \frac{x - 1}{3} ⩽ 2 \end{array}$ 的解为．

查看试题解析
14. 已知扇形的圆心角为60°，弧长为2πcm，则扇形的面积为cm² ．（计算结果保留π）

查看试题解析
15. 如图，已知Rt△AOC的直角顶点A落在x轴的正半轴上，且∠AOC＝30°，△OAC与△OBC关于直线OC对称，经过点C的反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象交射线OB于点D ，若BD＝1，则点C的坐标为．

查看试题解析
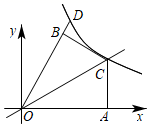16. 如图，有一个弓形的暗礁区AEB ，圆心角∠AOB＝120°，灯塔A在灯塔B的正西方向5 $\sqrt{3}$ 海里处，灯塔B的正北方向9海里处有一救援点C ，若救援船沿着东西方向巡逻时，离暗礁区最近点距离为海里；救援船向西巡逻至点F时，收到来自E点处某轮船的求救信号，测得点E在点F的南偏西60°方向，且∠FEO＝90°，救援船立即改变航向以30海里/小时的速度沿FE方向行驶，需小时到达点E ．

查看试题解析

三、解答题

17.

(1)、计算： $| - 2 | - \sqrt{16} + {(\sqrt{3} - 1)}^{0} - (- 3)$ ；

(2)、化简： $\frac{a + 2}{a^{2} - a} + \frac{3}{a - a^{2}}$ ．

查看试题解析
18. 如图，在△ABC和△EDF中，AC＝EF ， ∠ACB＝∠F＝90°，点A ， D ， B ， E在同一条直线上，且点D ， B分别为AB ， DE中点．

(1)、求证：△ABC≌△EDF ．

(2)、连接CD ，当CD＝5，EF＝6时，求BC的长．

查看试题解析
19. 质量检测部门对甲、乙两公司销售的某电子产品的使用寿命进行跟踪调查，各抽查了10件产品，统计结果如表：
甲公司被抽查的电子产品使用寿命统计表

时间（年）

6

7

8

10

11

数量（个）

2

3

2

2

1

乙公司被抽查的电子产品使用寿命统计表

时间（年）

5

6

9

11

13

数量（个）

2

4

1

1

2

(1)、求甲、乙两公司被抽查的电子产品的平均使用寿命．

(2)、若你是顾客，从平均数、中位数、众数的这三个角度进行分析，你将选购哪家公司销售的产品？

查看试题解析
20. 如图，在8×8的方格纸中，每个小方格的顶点称为格点，请按要求画格点四边形ABCD ．

(1)、在图1中画平行四边形ABCD ，使点P是它的对称中心．

(2)、在图2中画四边形ABCD ，使得∠D＝90°，且PB∥CD ．

查看试题解析
21. 如图，在平面直角坐标系中，二次函数y＝﹣x²＋bx＋c的图象与y轴交于点A（0，2），且对称轴是直线x＝2，过点A作x轴的平行线交抛物线于另一点B ．

(1)、求抛物线解析式，并根据该函数图象直接写出y＞2时x的取值范围．

(2)、已知点C是抛物线上一点且位于直线AB上方，若点C向左平移m个单位，将与抛物线上点D重合；若点D向下平移n个单位，将与x轴上点E重合．当m＋n＝ $\frac{7}{4}$ AB时，求点C坐标．

查看试题解析
22. 如图，在△ABC中，AC＝BC ，以BC为直径的⊙O交AB于点D ，交AC的延长线于点E ，连接DE交BC于点G ，过点D作DF⊥AC ，垂足为点F ，连接OD ．

(1)、求证：OD∥AE ．

(2)、若tan∠ODE＝ $\frac{1}{2}$ ，AE＝8，求CG的长．

查看试题解析
23. 温州市开展“明眸皓齿”工程以后，某商店准备购进A ， B两种护眼灯，已知每台护眼灯的进价A种比B种多40元，用2000元购进A种护眼灯和用1600元购进B种护眼灯的数量相同．

(1)、A ， B两种护眼灯每台进价各是多少元？

(2)、该商店计划用不超过14550元的资金购进A ， B两种护眼灯共80台，A ， B两种护眼灯的每台售价分别为300元和200元．
①若这两种护眼灯全部售出，则该商店应如何进货才能获得最大利润？最大利润是多少？

②若该商店捐赠8台护眼灯给温州市社会福利院，且剩余的护眼灯全部售出，现要使得80台护眼灯的利润率等于20%，则该商店应购进A ， B两种护眼灯各多少台？（利润率＝ $\frac{利润}{进价}$ ×100%）

查看试题解析
24. 如图，在矩形ABCD中，AD＝2 $\sqrt{5}$ ，AB＝4 $\sqrt{5}$ ，DM⊥AC于点M ，在对角线AC上取一点N ，使得2CN＝3AM ，连接DN并延长交BC于点E ， F是AB上一点，连接EF ， MF ．当点P从点E匀速运动到点F时，点Q恰好从点M匀速运动到点N ．

(1)、求AM ， CE的长．

(2)、若EF∥AC ，记EP＝x ， AQ＝y ．
①求y关于x的函数表达式．

②连接PQ ，当直线PQ平行于四边形DEFM的一边时，求所有满足条件的x的值．

(3)、在运动过程中，当直线PQ同时经过点B和D时，记点Q的运动速度为v₁ ，记点P的运动速度为v₂ ，求 $\frac{v_{1}}{v_{2}}$ 的值．

查看试题解析

时间（年）	6	7	8	10	11
数量（个）	2	3	2	2	1

时间（年）	5	6	9	11	13
数量（个）	2	4	1	1	2