浙江省温州市龙港市2021年中考数学一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
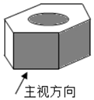
1. 计算8÷(﹣2)的结果是( )A、﹣4 B、﹣16 C、﹣6 D、102. 如图所示的一个六角螺帽毛坯底面正六边形的边长、高和内孔直径都相等,其主视图是( )
 A、
A、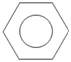 B、
B、 C、
C、 D、
D、 3. 2021年1月29日4时47分,我国长征四号丙火箭将3颗遥感三十一号卫星送入高度约为1100公里、与赤道存在63.4度倾角的轨道,发射任务取得圆满成功,数据1100用科学记数法表示为( )A、 B、 C、 D、4. 甲、乙和丙三位同学排成一排照相,则甲同学在乙丙之间的概率是( )A、 B、 C、 D、5. 如图,已知四边形ABCD内接于⊙O,连接OA,OC,若∠AOC=116°,则∠ADC的度数是( )
3. 2021年1月29日4时47分,我国长征四号丙火箭将3颗遥感三十一号卫星送入高度约为1100公里、与赤道存在63.4度倾角的轨道,发射任务取得圆满成功,数据1100用科学记数法表示为( )A、 B、 C、 D、4. 甲、乙和丙三位同学排成一排照相,则甲同学在乙丙之间的概率是( )A、 B、 C、 D、5. 如图,已知四边形ABCD内接于⊙O,连接OA,OC,若∠AOC=116°,则∠ADC的度数是( )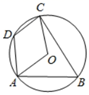 A、122° B、120° C、117° D、116°6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。
A、122° B、120° C、117° D、116°6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。株数(株)
7
9
12
2
花径(cm)
6.5
6.6
6.7
6.8
这批“金心大红”花径的众数为( )
A、6.5cm B、6.6cm C、6.7cm D、6.8cm7. 如图,升国旗时,某同学在离国旗18米处行注目礼,当国旗上升至顶端时,该同学视线的仰角为α°,已知双眼离地面1.6米,则旗杆AB的高度为( ) A、18tanα米 B、(18sinα+1.6)米 C、( +1.6)米 D、(18tanα+1.6)米8. 如图,在▱ABCD中,CD=10,∠ABC的平分线交AD于点E,过点A作AF⊥BE,垂足为点F,若AF=6,则BE的长为( )
A、18tanα米 B、(18sinα+1.6)米 C、( +1.6)米 D、(18tanα+1.6)米8. 如图,在▱ABCD中,CD=10,∠ABC的平分线交AD于点E,过点A作AF⊥BE,垂足为点F,若AF=6,则BE的长为( ) A、8 B、10 C、16 D、189. 已知二次函数y=﹣ +bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )A、5 B、7 C、12 D、﹣710. 勾股定理是几何中一个重要定理.著名数学家毕达哥拉斯用如图①所示的图形验证了勾股定理,把图①放入矩形内得到图②,∠ACB=90°,BC=2AC,E,F,G,H,I都在矩形MNOP的边上,则 的值为( )
A、8 B、10 C、16 D、189. 已知二次函数y=﹣ +bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )A、5 B、7 C、12 D、﹣710. 勾股定理是几何中一个重要定理.著名数学家毕达哥拉斯用如图①所示的图形验证了勾股定理,把图①放入矩形内得到图②,∠ACB=90°,BC=2AC,E,F,G,H,I都在矩形MNOP的边上,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:a2﹣2a+1= .12. 不等式组 的解集为.13. 某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有人.
 14. 半径为3的圆中,120°的圆心角所对的弧长为.15. 如图,在直角坐标系中,点A在反比例函数y= (k>0,x>0)的图象上,线段OA绕点A顺时针方向旋转90°得到线段AB,过点B向下作x轴的垂线,交该反比例函数图象于点C,连接AC,若△ABC的面积为1,tanB= ,则k的值为.
14. 半径为3的圆中,120°的圆心角所对的弧长为.15. 如图,在直角坐标系中,点A在反比例函数y= (k>0,x>0)的图象上,线段OA绕点A顺时针方向旋转90°得到线段AB,过点B向下作x轴的垂线,交该反比例函数图象于点C,连接AC,若△ABC的面积为1,tanB= ,则k的值为. 16. 工人师傅在正中间立着一根圆形排水管的正方形地面(如图①)铺瓷砖,先裁出四块全等直角三角形ABC的瓷砖如图②,再在AB边上各切割一个弓形(阴影部分),然后围着排水管拼接而成(不重叠,无缝隙)如图③所示.已知∠BAC=90°,切割点分别为A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8 , 依次连接这8个点恰好组成正八边形,AB﹣AC=(4+2 )cm,则AA1=cm;如果π取3,那么切去的每块弓形面积为cm2.
16. 工人师傅在正中间立着一根圆形排水管的正方形地面(如图①)铺瓷砖,先裁出四块全等直角三角形ABC的瓷砖如图②,再在AB边上各切割一个弓形(阴影部分),然后围着排水管拼接而成(不重叠,无缝隙)如图③所示.已知∠BAC=90°,切割点分别为A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8 , 依次连接这8个点恰好组成正八边形,AB﹣AC=(4+2 )cm,则AA1=cm;如果π取3,那么切去的每块弓形面积为cm2.
三、解答题
-
17.(1)、计算: +|﹣ |﹣40.(2)、解方程: =3.18. 如图,点A,B,C,D在同一条直线上,AB=CD,∠A=∠D,AE=DF.
 (1)、求证:△ACE≌△DBF.(2)、若BF⊥CE于点H,求∠HBC的度数.19. 今年3月5日是第58个“学习雷锋纪念日”,某校组织七、八年级全体学生开展“学习雷锋知识竞赛活动”.为了解竞赛成绩情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级80,80,85,85,90,90,90,95,95,100;八年级80,85,85,90,90,90,90,95,95,100.分析数据如表:
(1)、求证:△ACE≌△DBF.(2)、若BF⊥CE于点H,求∠HBC的度数.19. 今年3月5日是第58个“学习雷锋纪念日”,某校组织七、八年级全体学生开展“学习雷锋知识竞赛活动”.为了解竞赛成绩情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级80,80,85,85,90,90,90,95,95,100;八年级80,85,85,90,90,90,90,95,95,100.分析数据如表:平均数
中位数
众数
方差
七年级
a
90
90
39
八年级
90
90
b
30
根据以上信息回答下列问题:
(1)、求出表格中a,b的值;(2)、通过数据分析,你认为哪个年级的成绩比较好?请说明理由.20. 如图,在4×4的方格纸MNOP中,请在所给网格中按要求画格点四边形(顶点都在格点上,且均不与点M,N,O,P重合). (1)、在图1中画格点四边形ABCD,使点A,B,C,D分别落在MN,NO,OP,PM上,且对角线AC=BD,AC不垂直BD.(2)、在图2中画格点四边形EFGH,使点E,F,G,H分别落在MN,NO,OP,PM上,设它的两条对角线的夹角为α,且tanα=2.21. 二次函数y=ax2+bx+6的图象经过点(﹣2,0),(6,0).
(1)、在图1中画格点四边形ABCD,使点A,B,C,D分别落在MN,NO,OP,PM上,且对角线AC=BD,AC不垂直BD.(2)、在图2中画格点四边形EFGH,使点E,F,G,H分别落在MN,NO,OP,PM上,设它的两条对角线的夹角为α,且tanα=2.21. 二次函数y=ax2+bx+6的图象经过点(﹣2,0),(6,0). (1)、求二次函数的表达式和对称轴.(2)、如图,该二次函数图象交y轴于点A,点P在线段OA上,过点P作x轴的平行线交抛物线于B,C(点B在点C的左侧),若PC=5PB,求点P的纵坐标.22. 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足H在半径OB上,若劣弧CD沿着直线CD翻折,点B落在OA上的点E处(点E不与点A,O重合),连接CA,CE,CB.
(1)、求二次函数的表达式和对称轴.(2)、如图,该二次函数图象交y轴于点A,点P在线段OA上,过点P作x轴的平行线交抛物线于B,C(点B在点C的左侧),若PC=5PB,求点P的纵坐标.22. 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足H在半径OB上,若劣弧CD沿着直线CD翻折,点B落在OA上的点E处(点E不与点A,O重合),连接CA,CE,CB. (1)、求证:∠ACE=∠DCO.(2)、延长CE交⊙O于点M,连接AM,若AM=10,OE=3,求∠ACE的正弦值.23. 温州某商店以每件40元的价格购进一种商品,经市场调查发现:在一段时间内,该商品的日销售量y(件)与售价x(元/件)成一次函数关系,其对应关系如下表.
(1)、求证:∠ACE=∠DCO.(2)、延长CE交⊙O于点M,连接AM,若AM=10,OE=3,求∠ACE的正弦值.23. 温州某商店以每件40元的价格购进一种商品,经市场调查发现:在一段时间内,该商品的日销售量y(件)与售价x(元/件)成一次函数关系,其对应关系如下表.售价(元/件)
45
50
60
日销售量(件)
110
100
80
(1)、求y关于x的函数表达式.(2)、求售价为多少时,日销售利润最大,最大利润是多少元.(3)、该商店准备搞节日促销活动,顾客每购买一件该商品奖m元(m>0),要想在日销售量不少于68件时的日销售最大利润是1360元,若日销售量与售价仍然满足(1)中的函数关系,求m的值.(每件销售利润=售价﹣进价)24. 如图,一次函数y=﹣x+1的图象分别交x轴,y轴于A,B两点,C是线段OB上的动点(与O,B不重合),点D在AB上,∠BCD=∠ACO,过点D作DE⊥AC,交x轴于点E. (1)、求证: .(2)、当点E在线段OA上,以A为圆心,以AC为半径画圆,交y轴负半轴于点F,设OF=m,OE=n,求n关于m的函数表达式.(3)、连接CE,是否存在∠ECO=∠BAC?如果存在,请求出所有满足条件OC的长;如果不存在,请说明理由.
(1)、求证: .(2)、当点E在线段OA上,以A为圆心,以AC为半径画圆,交y轴负半轴于点F,设OF=m,OE=n,求n关于m的函数表达式.(3)、连接CE,是否存在∠ECO=∠BAC?如果存在,请求出所有满足条件OC的长;如果不存在,请说明理由.