浙江省绍兴市越城区2021年数学初中学业考试适应性试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 2是2的（）

A、相反数 B、倒数 C、绝对值 D、平方根

查看试题解析
2. 在⊙O中，已知半径为5，弦AB的长为8，则圆心O到AB的距离为（）

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，直线a∥b，∠1=60°，∠2=40°，则∠3等于（）

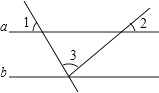A、40° B、60° C、80° D、100°

查看试题解析
4. 计算 ${(- 2 a)}^{2} \cdot a^{4}$ 的结果是（）

A、 $- 4 a^{6}$ B、 $4 a^{6}$ C、 $- 2 a^{6}$ D、 $- 4 a^{8}$

查看试题解析
5. 如图，已知 $△ A B C ， A B = A C$ ，以点B为圆心， $B C$ 长为半径画弧，交腰 $A C$ 于点E，则下列结论一定正确的是（）

A、 $B C = E C$ B、 $A E = B E$ C、 $∠ E B C = ∠ B A C$ D、 $∠ E B C = ∠ A B E$

查看试题解析
6. 已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的.那么安放的位置是（）

A、① B、② C、③ D、④

查看试题解析
7. 某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒，绿灯持续时间为60秒.若小明同学来到该路口遇到红灯，则至少需要等待15秒才会出现绿灯的概率为（）

A、 $\frac{7}{10}$ B、 $\frac{5}{8}$ C、 $\frac{3}{8}$ D、 $\frac{3}{10}$

查看试题解析
8. 小红同学在某数学兴趣小组活动期间，用铁丝设计并制作了如图所示的三种不同的图形，请您观察甲、乙、丙三个图形，判断制作它们所用铁丝的长度关系是（）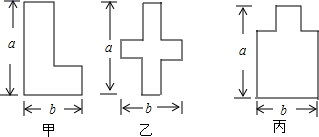

A、制作甲种图形所用铁丝最长 B、制作乙种图形所用铁丝最长 C、制作丙种图形所用铁丝最长 D、三种图形的制作所用铁丝一样长

查看试题解析
9. 如图，抛物线 $y = - x^{2} + a x + b$ 交x轴于 $A (1 ， 0) ， B (3 ， 0)$ 两点，点C是y轴的正半轴上一点，直线 $B C$ 交抛物线于点P，若点P是线段 $B C$ 的中点，那么 $\sin ∠ O C B$ 的值为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{3}{5}$

查看试题解析
10. 对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形每条边都至少有一个公共点（如图1），那么这个矩形水平方向的边长我们称为该图形的宽，矩形铅垂方向的边长我们称为该图形的高.如图2，已知菱形 $A B C D$ 的边长为1，菱形的边 $A B$ 水平放置，如果该菱形的高是宽的 $\frac{2}{3}$ ，那么菱形的宽是（）

A、 $\frac{18}{13}$ B、 $\frac{13}{9}$ C、 $\frac{3}{2}$ D、2

查看试题解析

二、填空题

11. 因式分解： $x y^{2} - 4 x$ = ．

查看试题解析
12. “植树节”时，九（2）班6个小组的植树棵数分别是： $5 、 7 、 3 、 x 、 6 、 4$ ，已知这组数据的众数是5，则这组数据的中位数为.

查看试题解析
13. 已知三个数1， $\sqrt{2}$ ，2，请再添上一个数，使它们构成一个比例式，满足这样条件的数是．

查看试题解析
14. 如图， $C D$ 是 $⊙ O$ 的弦，O是圆心，把 $⊙ O$ 的劣弧沿着 $C D$ 对折，A是对折后劣弧上的一点，若 $∠ C A D = 100 °$ ，那么 $∠ B C A + ∠ B D A =$ .

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = 3 ， B C = 4 ， P$ 是 $B C$ 边上的动点，设 $P C = x$ .若能在 $A C$ 边上找到一点Q，使 $∠ B Q P = 90 °$ ，则x的取值范围是.

查看试题解析
16. 在 $R t Δ A B C$ 中，∠C=90°，AC=2，BC=4，，点 $D ， E$ 分别是边 $B C$ 、 $A B$ 的中点，将 $Δ B D E$ 绕着点B旋转，点 $D ， E$ 旋转后的对应点分别为点 $D^{'} ， E^{'}$ ，当直线 $D^{'} ， E^{'}$ 经过点A时，线段 $C D^{'}$ 的长为

查看试题解析

三、解答题

17. 计算：

(1)、 ${(2 a - b)}^{2} - (4 a + b) (a - b)$ ；

(2)、 ${(- \frac{1}{2})}^{- 2} + {(2021 - π)}^{0} - \frac{\sqrt{3}}{3} \tan 60 °$ .

查看试题解析
18. 如图，一次函数 $y = m x + 5$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象在第一象限交于 $A (1 ， n)$ 和 $B (4 ， 1)$ 两点，过点A作y轴的垂线，垂足为M.

(1)、求一次函数和反比例函数的表达式；

(2)、求 $△ O A M$ 的面积S.

查看试题解析
19. 数学课中，张老师和同学们复习回顾圆与正多边形位置关系时，马伊同学向大家分享了自己设计的一个作圆内接等边三角形的方法，方法如下：

①如图，作直径 $A D$ ；

②作半径 $O D$ 的垂直平分线，交 $⊙ O$ 于 $B 、 C$ 两点；

③连结 $A B 、 A C$ ，那么 $△ A B C$ 为所求的三角形.

张老师认可马伊同学的设计，请您顺着马伊同学的设计思路完成整个过程.

(1)、用尺规在原图上作出 $△ A B C$ ；

(2)、证明 $△ A B C$ 是等边三角形.

查看试题解析
20. 如图1是城市广场地下停车场的入口，图2是安装雨棚左侧支架的示意图.已知，支架的立柱 $B C$ 与地面垂直，即 $∠ B C A = 90 °$ ，且 $B C = 1.5 m$ ，点 $F 、 A 、 C$ 在同一条水平线上，斜杆 $A B$ 与水平线 $A C$ 的夹角 $∠ B A C = 30 °$ ，支撑杆 $D E ⊥ A B$ 于点D，该支架的边 $B E$ 与 $A B$ 的夹角 $∠ E B D = 60 °$ ，又测得 $A D = 1 m$ .请你求出该支架的边 $B E$ 及顶端E到地面的距离 $E F$ 的长度.

查看试题解析
21. 某手机店在今年的1~4月这四个月时间里，试销售 $A 、 B$ 两个品牌的手机，合计售出400台，试销结束后，经销人员统计并绘制出两幅不同类型的不完整统计图，如图1和图2所示.

(1)、求出B品牌手机第三个月销售量和第四个月两品牌的销量占总销量的百分比；

(2)、为跟踪调查手机的使用稳定性，从售出的第四个月 $A 、 B$ 两个品牌的手机中，随机抽取一台，求抽到B品牌手机的概率；

(3)、请在图2中补全表示B品牌手机月销量的折线，并结合折线的走势进行简要分析，帮助该店判断应在 $A 、 B$ 中选择哪个品牌作为经销商品.

查看试题解析
22. 如图，已知 $A B$ 与 $⊙ O$ 相切于点A，直线 $l$ 与 $⊙ O$ 相离， $O B ⊥ l$ 于点B，且 $O B = 5 ， O B$ 与 $⊙ O$ 交于点 $P ， A P$ 的延长线交直线 $l$ 于点C.

(1)、求证： $A B = B C$ ；

(2)、若 $⊙ O$ 的半径为3，求线段 $A P$ 的长.

查看试题解析
23. 在平面直角坐标系xOy中，如果抛物线 $y = a x^{2} + b x + c$ 上存在一点A，使点A关于坐标原点O的对称点 $A^{'}$ 也在这条抛物线上，那么我们把这条抛物线叫做回归抛物线，点A叫做这条抛物线的回归点.

(1)、已知点M在抛物线 $y = - x^{2} + 2 x + 4$ 上，且点M的横坐标为2，试判断抛物线 $y = - x^{2} + 2 x + 4$ 是否为回归抛物线，并说明理由；

(2)、已知点C为回归抛物线 $y = - x^{2} - 2 x + c$ 的顶点，如果点C是这条抛物线的回归点，求这条抛物线的表达式；

(3)、在（2）的条件下，所求得的抛物线的对称轴与x轴交于点D.连接CO并延长，交该抛物线于点E.点F是射线CD上一点，如果 $∠ C F E = ∠ D E C$ ，求点F的坐标.

查看试题解析
24. 如图，已知在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 4$ ，点D为边 $B C$ 上一动点（与点B、C不重合），点E为边 $A B$ 上一点， $∠ E D B = ∠ A D C$ ，过点E作 $E F ⊥ A D$ ，垂足为点G，交射线 $A C$ 于点F．

(1)、如果点D为边 $B C$ 的中点，求 $∠ D A B$ 的正切值；

(2)、当点F在边 $A C$ 上时，设 $C D = x$ ， $C F = y$ ，求y关于x的函数解析式及定义域；

(3)、联结 $D F$ 如果 $△ C D F$ 与 $△ A G E$ 相似，求线段 $C D$ 的长．

查看试题解析