浙江省杭州市下城区2021年数学中考一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 化简：2m－3m＝（）

A、m B、－m C、5m D、－5m

查看试题解析
2. 若 $\frac{3 x - 1}{2} = 1$ ，则（）

A、 $3 x = 2 + 1$ B、 $3 x = 1 - 2$ C、 $3 x - 1 = \frac{1}{2}$ D、 $3 x - 1 = 1$

查看试题解析
3. 下列计算结果是负数的是（）

A、 $2^{- 3}$ B、 $3^{- 2}$ C、 ${(- 2)}^{3}$ D、 ${(- 3)}^{2}$

查看试题解析
4. 如图，在△ABC中，点D ，点E分别在边AB ， AC上（不与端点重合），连接DE ，若DE∥BC ，则 $\frac{D E}{B C}$ ＝（）

A、 $\frac{A D}{D B}$ B、 $\frac{E C}{A E}$ C、 $\frac{A D}{A B}$ D、 $\frac{E C}{A C}$

查看试题解析
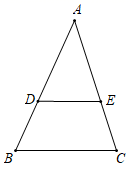5. 设一个直角三角形的两直角边分别是a ， b ，斜边是c ．若用一把最大刻度是20cm的直尺，可一次直接测得c的长度，则a ， b的长可能是（）

A、a＝12，b＝16 B、a＝11，b＝17 C、a＝10，b＝18 D、a＝9，b＝19

查看试题解析
6. 甲烧杯有432毫升酒精，乙烧杯有96毫升酒精，若从甲烧杯倒x毫升酒精到乙烧杯后，此时，甲烧杯中的酒精是乙烧杯中的酒精的2倍，则（）

A、432＝2（96＋x） B、432－x＝2×96 C、432－x＝2（96＋x） D、432＋x＝2（96－x）

查看试题解析
7. 某公司六位员工的月工资分别是4000元，5000元，5000元，5500元，7000元，10000元，这些数据的（）

A、中位数＞众数＞平均数 B、中位数＞平均数＞众数 C、平均数＞众数＞中位数 D、平均数＞中位数＞众数

查看试题解析
8. 若a＜0＜b＜c ，则（）

A、a＋b＋c是负数 B、a＋b－c是负数 C、a－b＋c是正数 D、a－b－c是正数

查看试题解析
9. 如图，直角三角形ABC的顶点A在直线m上，分别度量：①∠1，∠2，∠C；②∠2，∠3，∠B；③∠3，∠4，∠C；④∠1，∠2，∠3，可判断直线m与直线n是否平行的是（）

A、① B、② C、③ D、④

查看试题解析
10. 设二次函数 $y = x^{2} - k x + 2 k$ （ $k$ 为实数）的图象过点 $(1， y_{1})$ ， $(2， y_{2})$ ， $(3 ， y_{3})$ ， $(4 ， y_{4})$ ，设 $y_{1} - y_{2} = a$ ， $y_{3} - y_{4} = b$ ，（）

A、若 $a b < 0$ ，且 $a + b < 0$ ，则 $k < 3$ B、着 $a b < 0$ ，且 $a + b > 0$ ，则 $k < 5$ C、若 $a b > 0$ ，且 $a + b < 0$ ，则 $k > 3$ D、若 $a b > 0$ ，且 $a + b > 0$ ，则 $k > 7$

查看试题解析

二、填空题

11. 因式分解： $a^{2} - a b =$ ．

查看试题解析
12. 如图，点A ，点B ，点C在⊙O上，分别连接AB ， BC ， OC ．若AB＝BC ， ∠B＝40°，则∠OCB＝．

查看试题解析
13. 一个仅装有球的不透明布袋里共有3个球（只有颜色不同），其中2个是红球，1个是白球．从中同时摸出两个球，都是红球的概率是．

查看试题解析
14. 在等腰三角形ABC中，∠B＝30°，若AB＞BC ．则∠C＝．

查看试题解析
15. 设矩形的两条邻边长分别为x ， y ，且满足 $y = \frac{3}{x}$ ．若此矩形能被分割成3个全等的正方形，则这个矩形的对角线长是．

查看试题解析
16. 如图，点E ，点F分别在矩形ABCD的边AB ， AD上，连接AC ， CE ， CF ．若CE是△ACB的角平分线，CF是△ACD的中线，且∠BCE＝∠FCD ，则 $\frac{A B}{B C}$ ＝．

查看试题解析

三、解答题

17. 某校为了解九年级学生作业量情况，某天随机抽取了50名九年级学生进行调查，并把调查结果绘制成不完整的频数分布直方图（每组含前一个边界值，不含后一个边界值），如下图，已知所有学生作业完成时间均在0.5小时~2.5小时（含0.5小时，不含2.5小时）的范围内．

(1)、设图中缺少部分的频数为a ，求a的值．

(2)、补全频数分布直方图．

(3)、该校共有九年级学生500人，估计这天作业完成时间小于1小时的人数．

查看试题解析
18. 如图，在Rt△ABC中，∠BAC＝90°，AB＝15，BC＝25，AD是BC边上的高，点E在边AC上，EF⊥BC于点F ．

(1)、求证：sinB＝sin∠CEF ．

(2)、若AE＝5，求证：△ABD≌△CEF ．

查看试题解析
19. 已知x－2y＋z＝2x－y＋z＝3，且x ， y ， z的值中仅有一个为0，解这个方程组．

查看试题解析
20. 某列“复兴号”高铁从A站出发，以350km/h的速度向B站匀速行驶（途中不停靠），设行驶的时间为t（h），所对应的行驶路程为s（km）．

(1)、写出s关于t的函数表达式．

(2)、已知B站距离A站1400km，这列高铁在上午7点时离开A站．
①几点到达B站？

②若C站在A站和B站之间，且B ， C两站之间的距离为300km，借助所学的数学知识说明：列车途经C站时，已过上午10点．

查看试题解析
21. 如图，在△ABC中，AD是角平分线，点E ，点F分别在线段AB ， AD上，且∠EFD＝∠BDF ．

(1)、求证：△AFE∽△ADC ．

(2)、若 $\frac{A E}{A C} = \frac{4}{5}$ ， $\frac{A E}{E B} = 2$ ，且∠AFE＝∠C ，探索BE和DF之间的数量关系．

查看试题解析
22. 设二次函数y＝（x－m）（x－m－2），其中m为实数．

(1)、若函数y的图象经过点A（4，3），求函数y的表达式．

(2)、若函数y的图象的对称轴是直线x＝1，求该函数的最小值．

(3)、把函数y的图象向上平移k个单位，所得图象与x轴没有交点，求证：k＞1．

查看试题解析
23. 如图，AB ， CD是⊙O的两条直径，且AB⊥CD ，点E ，点F分别在半径OC ， OD上（不与点O ，点C ，点D重合），连接AE ， EB ， BF ， FA ．

(1)、若CE＝DF ，求证：四边形AEBF是菱形．

(2)、过点O作OG⊥EB ，分别交EB ， ⊙O于点H ，点G ，连接BG ．
①若∠COG＝∠EBG ，判断△OBG的形状，说明理由．

②若点E是OC的中点，求 $\frac{G H}{H O}$ 的值．

查看试题解析