四川省宜宾市长宁县2021年九年级下学期数学中考一诊试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的倒数是（）

A、 $\frac{1}{3}$ B、-3 C、 $- \frac{1}{3}$ D、 $\pm \frac{1}{3}$

查看试题解析
2. 新型冠状病毒属于 $β$ 属的新型冠状病毒，有包膜，颗粒呈圆形或者椭圆形，常为多形性，最大直径约 $0.0000014$ 米，将 $0.0000014$ 用科学记数法表示为（）

A、 $1.4 \times 10^{- 5}$ B、 $1.4 \times 10^{- 6}$ C、 $1.4 \times 10^{- 7}$ D、 $14 \times 10^{- 6}$

查看试题解析
3. 如图，立体图形的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中，计算错误的是（）

A、 $2 a + 3 a = 5 a$ B、 $- x^{2} \cdot x = - x^{3}$ C、 $2 x - 3 x = - 1$ D、 ${(- x^{3})}^{2} = x^{6}$

查看试题解析
5. 把某不等式组中两个不等式的解集表示在数轴上，如图所示，则这个不等式组可能是（）

A、 ${\begin{matrix} x > 4 \\ x \leq - 1 \end{matrix}$ B、 ${\begin{matrix} x \leq 4 \\ x > - 1 \end{matrix}$ C、 ${\begin{matrix} x > 4 \\ x > - 1 \end{matrix}$ D、 ${\begin{matrix} x < 4 \\ x \geq - 1 \end{matrix}$

查看试题解析
6. 今年3月，我市某公司举行考试招聘，其中8名应聘者的基本能力得分如下表所示：

得分

80

85

87

90

人数

1

3

2

2

则这8名应聘者的基本能力得分的众数、中位数分别是（）

A、85、85 B、87、85 C、85、86 D、85、87

查看试题解析
7.
如图，直线AB、CD相交于点E，DF∥AB．若∠D=70°，则∠CEB等于（　　）

A、70° B、80° C、90° D、110°

查看试题解析
8. 已知点 $M$ 是直线 $y = x + 1$ 上一点， $M$ 的横坐标为1，若点N与点 $M$ 关于 $y$ 轴对称，则点N的坐标为（）

A、 $(1 ， - 2)$ B、 $(- 1 ， - 2)$ C、 $(- 2 ， 1)$ D、 $(- 1 ， 2)$

查看试题解析
9. 若关于x的一元二次方程的两个根为x₁=1，x₂=2，则这个方程可能是（）

A、x²-3x+2=0 B、x²+3x+2=0 C、x²+3x-2=0 D、x²-2x+3=0

查看试题解析
10. 在 $△ A B C$ 中， $D$ 、 $E$ 两点分别在 $A B$ 、 $A$ 边上， $D E // B C$ .若 $A D ： D B = 2 ： 1$ ，则 $S_{△ A D E} ： S_{△ A B C}$ 为（）

A、 $2 ： 3$ B、 $4 ： 9$ C、 $4 ： 5$ D、 $4 ： 1$

查看试题解析
11. “圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小.以锯锯之，深一寸，锯道长六寸，问径几何？”用现在的数学语言表述是：“如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为 $E$ ， $C E = 1$ 寸， $A B = 6$ 寸，求直径 $C D$ 的长”.依题意， $C D$ 长为（）

A、13寸 B、12寸 C、10寸 D、8寸

查看试题解析
12. 如图， $A$ ， $B$ ， $E$ 三点在同一直线上， $△ A B C$ ， $△ C D E$ 都是等边三角形，连接 $A D$ ， $B E$ ， $O C$ ：下列结论中正确的是（）
①△ACD≌△BCE；②△CPQ是等边三角形；③ $O C$ 平分 $∠ A O E$ ；④△BPO≌△EDO.

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

13. 因式分解： $3 y^{2} - 27 =$ .

查看试题解析
14. 不等式 $3 x - 10 \leq 0$ 的非负整数解是.

查看试题解析
15. 若方程组 ${\begin{array}{l} 2 x + y = b \\ x - b y = a \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 0 \end{array}$ ，那么|a-b|= ．

查看试题解析
16. 前年“五•一”期间，一批大二同学包租一辆客车去蜀南花海游览，客车的租金为500元，出发时，又增加了5名同学，且租金不变，这样每个同学比原来少分摊了5元车费，若设原来参加游览的同学一共有 $x$ 人，为求 $x$ ，可列方程为.

查看试题解析
17. 某直角三角形的周长为15，斜边长为7，该直角三角形的面积是.

查看试题解析
18. 给出定义：设一条直线与一条抛物线只有一个公共点，且这条直线与这条抛物线的对称轴不平行，就称直线与抛物线相切，这条直线是抛物线的切线.有下列命题：
①直线 $y = 0$ 是抛物线 $y = \frac{1}{4} x^{2}$ 的切线；

②直线 $x = - 2$ 与抛物线 $y = \frac{1}{4} x^{2}$ 相切于点 $(- 2 ， 1)$

③若直线 $y = x + b$ 与抛物线 $y = \frac{1}{4} x^{2}$ 相切，则相切于点 $(2 ， 1)$

④若直线 $y = k x - 2$ 与抛物线 $y = \frac{1}{4} x^{2}$ 相切，则实数 $k = \sqrt{2}$

其中正确命题有.

查看试题解析

三、解答题

19.

(1)、计算： ${(\frac{1}{2})}^{- 1} - {(π - 3)}^{0} + {(- 1)}^{2021} - \cos 60 °$

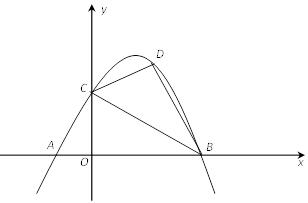
(2)、化简： $\frac{x^{2} - x}{x^{2} - 1} + (1 - \frac{1}{x + 1})$

查看试题解析
20. 如图，分别过点 $C$ 、 $B$ 作 $△ A B C$ 的 $B C$ 边上的中线 $A D$ 及其延长线的垂线，垂足分别为 $E$ 、 $F$ .

(1)、求证： $B F = C E$ ；

(2)、若 $△ A C E$ 的面积为4， $△ C E D$ 的面积为3，求△ABF的面积.

查看试题解析
21. 我市某中学举行“法制进校园”知识竞赛，赛后将学生的成绩分为A、B、C、D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.

(1)、成绩为“ $B$ 等级”的学生人数有 ▲ 名，并把条统计图补充完整；

(2)、在扇形统计图中，表示“ $D$ 等级”的扇形的圆心角度数为，图中 $m$ 的值为.

(3)、学校决定从本次比赛获得“ $A$ 等级”的学生中，选出2名去参加市中学生知识竞赛.已知“ $A$ 等级”中有1名女生，请用列表或画树状图的方法求出女生被选中的概率.

查看试题解析
22. 为了维护我国海洋权力，海监部门对我国领海实行了常态化巡航管理.如图，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在 $A$ 处测得灯塔 $P$ 在北偏东 $60 °$ 方向上，海监船继续向东航行1小时到达 $B$ 处，此时测得灯塔 $P$ 在北偏东 $30 °$ 方向上.

(1)、求 $B$ 处到灯塔 $P$ 的距离；

(2)、已知灯塔 $P$ 的周围50海里内有暗礁，若海监船继续向正东方向航行是否安全？（参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ， $\sqrt{5} \approx 2.236$ ）

查看试题解析
23. 如图，已知反比例函数y= $\frac{m}{x}$ （m≠0）的图象经过点（1，4），一次函数y=﹣x+b的图象经过反比例函数图象上的点Q（﹣4，n）.

(1)、求反比例函数与一次函数的表达式；

(2)、一次函数的图象分别与x轴、y轴交于A、B两点，与反比例函数图象的另一个交点为P点，连结OP、OQ，求△OPQ的面积.

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $∠ B = ∠ C A D$ .

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若点 $E$ 是 $\overset{⌢}{B D}$ 的中点，连接 $A E$ 交 $B C$ 于点 $F$ ，当 $B D = 5$ ， $C D = 4$ 时，求 $A F$ 的值.

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 经过A（-1，0）、B（4，0）、C（0，2）三点，点D（x ， y）为抛物线上第一象限内的一个动点．

(1)、求抛物线所对应的函数表达式；

(2)、当 $Δ B C D$ 的面积为3时，求点D的坐标；

(3)、过点D作 $D E ⊥ B C$ ，垂足为点E ，是否存在点D ，使得 $Δ C D E$ 中的某个角等于 $∠ A B C$ 的2倍？若存在，求点D的横坐标；若不存在，请说明理由．

查看试题解析

得分	80	85	87	90
人数	1	3	2	2