四川省绵阳市三台县2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 古钱币是我国悠久的历史文化遗产,以下是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )
 A、
A、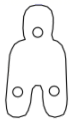 B、
B、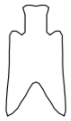 C、
C、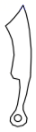 D、
D、 2. 起重机将质量为6.5t的货物沿竖直方向提升了2m,则起重机提升货物所做的功用科学记数法表示为(g=10N/kg)A、1.3×106J B、13×105J C、13×104J D、1.3×105J3. 用一把带有刻度的直尺,① 可以画出两条平行的直线
2. 起重机将质量为6.5t的货物沿竖直方向提升了2m,则起重机提升货物所做的功用科学记数法表示为(g=10N/kg)A、1.3×106J B、13×105J C、13×104J D、1.3×105J3. 用一把带有刻度的直尺,① 可以画出两条平行的直线 与b,如图⑴;② 可以画出∠AOB的平分线OP,如图⑵所示;③ 可以检验工件的凹面是否为半圆,如图⑶所示;④ 可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有( )
与b,如图⑴;② 可以画出∠AOB的平分线OP,如图⑵所示;③ 可以检验工件的凹面是否为半圆,如图⑶所示;④ 可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有( ) 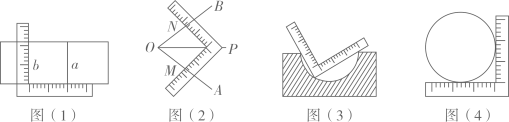 A、1个 B、2个 C、3个 D、4个4. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A、1个 B、2个 C、3个 D、4个4. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )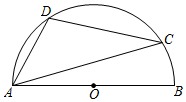 A、10° B、14° C、16° D、26°5. 如图,矩形ABCD的顶点A和对称中心在反比例函数 (k≠0,x>0),若矩形ABCD的面积为10,则k的值为( )
A、10° B、14° C、16° D、26°5. 如图,矩形ABCD的顶点A和对称中心在反比例函数 (k≠0,x>0),若矩形ABCD的面积为10,则k的值为( )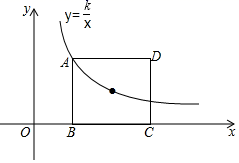 A、10 B、4 C、3 D、56. 定义运算:若am=b,则logab=m(a>0),例如23=8,则log28=3.运用以上定义,计算:log5125﹣log381=( )A、﹣1 B、2 C、1 D、447. 将抛物线M:y=- x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )A、45° B、60° C、90° D、120°8. 如图,△ABC、△FED区域为驾驶员的盲区,驾驶员视线PB与地面BE的央角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F为视线与车窗底端的交点,AF BE,AC⊥BE,FD⊥BE.若A点到B点的距离AB=1.6m,则盲区中DE的长度是( )(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)
A、10 B、4 C、3 D、56. 定义运算:若am=b,则logab=m(a>0),例如23=8,则log28=3.运用以上定义,计算:log5125﹣log381=( )A、﹣1 B、2 C、1 D、447. 将抛物线M:y=- x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )A、45° B、60° C、90° D、120°8. 如图,△ABC、△FED区域为驾驶员的盲区,驾驶员视线PB与地面BE的央角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F为视线与车窗底端的交点,AF BE,AC⊥BE,FD⊥BE.若A点到B点的距离AB=1.6m,则盲区中DE的长度是( )(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)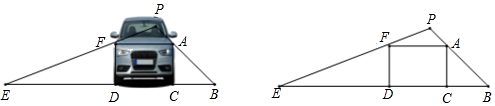 A、2.6m B、2.8m C、3.4m D、4.5m9. 设方程x2+x﹣1=0的一个正实数根为a,2a3+a2﹣3a的值是( )A、1 B、﹣1 C、2 D、﹣310. 如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,则线段EF的最大值为( )
A、2.6m B、2.8m C、3.4m D、4.5m9. 设方程x2+x﹣1=0的一个正实数根为a,2a3+a2﹣3a的值是( )A、1 B、﹣1 C、2 D、﹣310. 如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,则线段EF的最大值为( )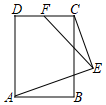 A、7 B、8 C、9 D、1011. 若数a使关于x的不等式组 有且仅有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、﹣3 B、﹣2 C、﹣1 D、112. 如图,在正方形ABCD中,点O为对角线AC的中点,过点O作射线OG、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
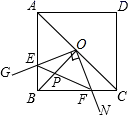
A、7 B、8 C、9 D、1011. 若数a使关于x的不等式组 有且仅有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、﹣3 B、﹣2 C、﹣1 D、112. 如图,在正方形ABCD中,点O为对角线AC的中点,过点O作射线OG、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
(1)图形中全等的三角形只有两对;(2)正方形ABCD的面积等于四边形OEBF面积的4倍;(3)BE+BF= OA;(4)AE2+CF2=2OP•OB.正确的结论有( )个.
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
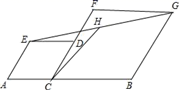
13. 分解因式:3x2﹣6xy+3y2= .14. 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是.
 15. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm.
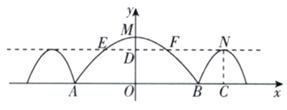
15. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm. 16. 如图所示,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度 为 ,顶点M距水面 (即 ),小孔顶点N距水面 (即 ).当水位上涨到刚好淹没小孔时,借助图中的直角坐标系,可以得出此时大孔的水面宽度 是m.
16. 如图所示,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度 为 ,顶点M距水面 (即 ),小孔顶点N距水面 (即 ).当水位上涨到刚好淹没小孔时,借助图中的直角坐标系,可以得出此时大孔的水面宽度 是m.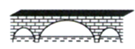
 17. 普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的倍.18. 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),且与x轴交点的横坐标为x1、x2 , 其中﹣2<x1<﹣1,0<x2<1,则下列结论:①2a﹣b<0,②4a﹣2b+c>0,③b2+8a>4ac,④当x>0时,函数值随x的增长而减少,⑤a+c<1.其中正确的是(填序号).
17. 普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的倍.18. 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),且与x轴交点的横坐标为x1、x2 , 其中﹣2<x1<﹣1,0<x2<1,则下列结论:①2a﹣b<0,②4a﹣2b+c>0,③b2+8a>4ac,④当x>0时,函数值随x的增长而减少,⑤a+c<1.其中正确的是(填序号).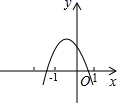
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中x,y的取值是二元一次方程x+2y=7的一对整数解.21. 年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通, 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域( 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
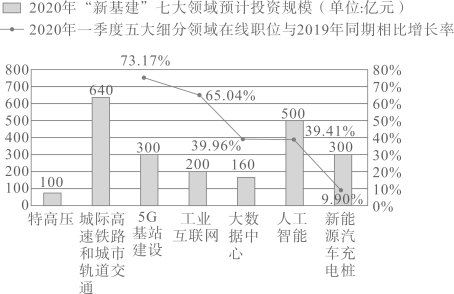 (1)、填空:图中 年“新基建”七大领域预计投资规模的中位数是亿元;(2)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么;(3)、小勇对“新基建”很感兴趣,他收集到了五大细分领域的图标,依次制成编号为 , , , , 的五张卡片(除编号和内容外,其余完全相同),将这五张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法求抽到的两张卡片恰好是编号为 ( 基站建设)和 (人工智能)的概率.
(1)、填空:图中 年“新基建”七大领域预计投资规模的中位数是亿元;(2)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么;(3)、小勇对“新基建”很感兴趣,他收集到了五大细分领域的图标,依次制成编号为 , , , , 的五张卡片(除编号和内容外,其余完全相同),将这五张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法求抽到的两张卡片恰好是编号为 ( 基站建设)和 (人工智能)的概率. 22. Rt△ABC在直角坐标系内的位置如图所示,反比例函数 在第一象限内的图象与BC边交于点D(4,m),与AB边交于点E(2,n),△BDE的面积为2.
22. Rt△ABC在直角坐标系内的位置如图所示,反比例函数 在第一象限内的图象与BC边交于点D(4,m),与AB边交于点E(2,n),△BDE的面积为2.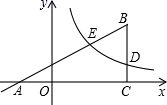 (1)、求m与n的数量关系;(2)、当tan∠BAC= 时,求反比例函数的解析式和直线AB的解析式;(3)、设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B,C,P为顶点的三角形与△EDB相似?若存在,求出此时点P的坐标;若不存在,请说明理由.23. 如图,在 中, ,AD平分 ,AD交BC于点D, 交AB于点E, 的外接圆⊙O交AC于点F,连接EF.
(1)、求m与n的数量关系;(2)、当tan∠BAC= 时,求反比例函数的解析式和直线AB的解析式;(3)、设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B,C,P为顶点的三角形与△EDB相似?若存在,求出此时点P的坐标;若不存在,请说明理由.23. 如图,在 中, ,AD平分 ,AD交BC于点D, 交AB于点E, 的外接圆⊙O交AC于点F,连接EF.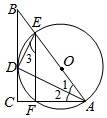 (1)、求证:BC是⊙O的切线;(2)、求⊙O的半径r及 的正切值.24. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1)、求证:BC是⊙O的切线;(2)、求⊙O的半径r及 的正切值.24. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示. (1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.25. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.25. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.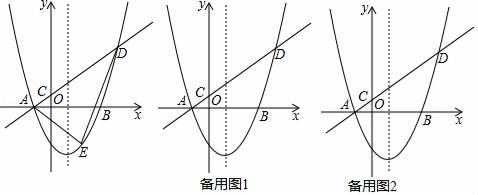 (1)、直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).(2)、点E为直线l下方抛物线上一点,当△ADE的面积的最大值为 时,求抛物线的函数表达式;(3)、设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.26. 如图,在正方形ABCD中,AB=4,动点P从点A出发,以每秒2个单位的速度,沿线段AB方向匀速运动,到达点B停止.连接DP交AC于点E,以DP为直径作⊙O交AC于点F,连接DF、PF.
(1)、直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).(2)、点E为直线l下方抛物线上一点,当△ADE的面积的最大值为 时,求抛物线的函数表达式;(3)、设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.26. 如图,在正方形ABCD中,AB=4,动点P从点A出发,以每秒2个单位的速度,沿线段AB方向匀速运动,到达点B停止.连接DP交AC于点E,以DP为直径作⊙O交AC于点F,连接DF、PF.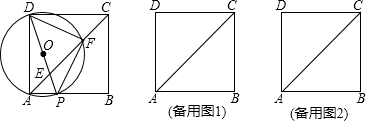 (1)、求证:△DPF为等腰直角三角形;(2)、若点P的运动时间t秒.
(1)、求证:△DPF为等腰直角三角形;(2)、若点P的运动时间t秒.①当t为何值时,点E恰好为AC的一个三等分点;
②将△EFP沿PF翻折,得到△QFP,当点Q恰好落在BC上时,求t的值.