四川省成都市郫都区2021年数学中考一诊试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 我国古代著作《九章算术》在世界数学史上首次正式引入负数，若气温升高 $3^{°} C$ 时，气温变化记作 $+ 3^{°} C$ ，那么气温下降 $10^{°} C$ 时，气温变化记作（）

A、 $- 13^{°} C$ B、 $- 10^{°} C$ C、 $- 7^{°} C$ D、 $+ 7^{°} C$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 $a^{- 2} = - a^{2}$ C、 ${(a^{2})}^{4} = a^{8}$ D、 $a^{4} \div a^{4} = a$

查看试题解析
4. 如图，在 $△ A B C$ 中，点 $D$ 是 $A B$ 上一点， $D E // B C$ 交 $M C$ 于点 $E$ ， $A D = 3$ ， $B D = 2$ ，则 $A E$ 与 $E C$ 的比是（）

A、 $3 ： 2$ B、 $3 ： 5$ C、 $9 ： 16$ D、 $9 ： 4$

查看试题解析
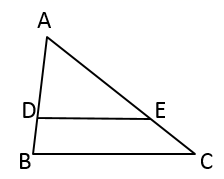5. 如图所示，点A、B、C都在 $⊙ O$ 上，若 $∠ A B O = 20 ° ， ∠ A C O = 30 °$ ，则 $∠ B O C =$ （）

A、 $100 °$ B、 $110 °$ C、 $125 °$ D、 $130 °$

查看试题解析
6. 如图所示的几何体是由两个相同的正方体和一个圆锥搭建而成，其左视图是（）

A、 B、 C、 D、

查看试题解析
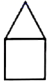7. 习近平总书记提出了五年“精准扶贫”的战略构想，意味着每年要减贫约11600000人，将数据11600000用科学记数法表示为（）

A、 $1.16 \times 10^{6}$ B、 $1.16 \times 10^{7}$ C、 $1.16 \times 10^{8}$ D、 $11.6 \times 10^{6}$

查看试题解析
8. 一个足球队23名队员的年龄统计结果如下表所示，这个足球队队员年龄的众数，中位数分别是（）

年龄/岁

12

13

14

15

16

人数/人

2

4

5

7

5

A、14，15 B、14，14 C、15，13 D、15，15

查看试题解析
9. 若点 $A (m, y_{1})$ ，点 $B (m + a^{2} + 1, y_{2})$ 都在一次函数 $y = 5 x + 4$ 的图象上，则（）

A、 $y_{1} < y_{2}$ B、 $y_{1} = - y_{2}$ C、 $y_{1} > y_{2}$ D、 $y_{1} = y_{2}$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的图象如图，下列结论：① $a < 0$ ；② $2 a + b = 0$ ；③ $b^{2} - 4 a c < 0$ ；④ $4 a + 2 b + c < 0$ .其中正确的有（）

A、1个 B、3个 C、2个 D、4个

查看试题解析

二、填空题

11. 计算： ${(2021 - π)}^{0} =$ .

查看试题解析
12. 将点 $P (- 3, 1)$ 向上平移2个单位长度得到点Q，则点Q的坐标为．

查看试题解析
13. 如图，在平行四边形ABCD中， $A B / / C D$ ，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于 $\frac{1}{2} M N$ 长为半径作弧，两弧相交于点P；③作射线AP，交边CD于点Q，若 $∠ D = 110 °$ ，则 $∠ A Q D$ 的度数为.

查看试题解析
14. 若关于x的方程 $\frac{x + m}{x - 4} + \frac{3 m}{4 - x} = 3$ 的解为正数，则m的取值范围是.

查看试题解析
15. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
16. 若 $m$ ， $n$ 是方程 $x^{2} + 2 x - 2021 = 0$ 的两个实数根，则 $m^{2} + 3 m + n$ 的值为.

查看试题解析
17. 如图，有A、B、C三类长方形（或正方形）卡片（a＞b），其中甲同学持有A、B类卡片各一张，乙同学持有B、C类卡片各一张，丙同学持有A、C类卡片各一张，现随机选取两位同学手中的卡片共四张进行拼图，则能拼成一个正方形的概率是.

查看试题解析
18. 如图，已知正方形ABCD中，两动点M和N分别从顶点B、C同时出发，以相同的速度沿BC、CD向终点C、D运动，连接AM、BN，交于点P，再连接PC，若 $A B = 4$ ，则PC长的最小值为.

查看试题解析
19. 平面直角坐标系 $x O y$ 中，矩形ABOC的顶点 $A (4 ， 3)$ ，点B在x轴上，双曲线 $y = k x^{- 1} (k > 0)$ 分别交两边AC，AB于E、F两点（E、F不与A重合），沿着EF将矩形ABOC折叠使A、D两点重合.若折叠后， $△ A B D$ 是等腰三角形，则此时点D的坐标为.

查看试题解析

三、解答题

20.

(1)、计算： $3 \tan 30 ° - \sqrt{12} - \sqrt{2} \sin 45^{°} + 3 \sqrt{\frac{1}{3}}$ .

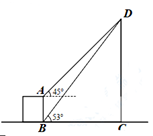
(2)、解不等式组： ${\begin{array}{l} 3 (x - 2) \leq 4 ① \\ x + 1 > \frac{2 x - 1}{5} ② \end{array}$ .

查看试题解析
21. 如图，从楼层底部B处测得旗杆CD的顶端D处的仰角是53°，从楼层顶部A处测得旗杆CD的顶端D处的仰角是45°，已知楼层AB的楼高为3米。求旗杆CD的高度约为多少米？(参考数据： sin53°≈ $\frac{4}{5}$ ，cos53°≈ $\frac{3}{5}$ ，tan53°≈ $\frac{4}{3}$ )

查看试题解析
22. 先化简，再求值： $(1 + \frac{m}{m^{2} - m}) \div \frac{m^{2} - 1}{m^{2} - 2 m + 1}$ ，其中m从﹣1、0、1、2这四个数中选取.

查看试题解析
23. 某校为了解九年级学生对新冠肺炎防控知识的掌握情况，从全校九年级学生中随机抽取部分学生做为样本进行调查.

根据图中提供的不完整信息，解答下列问题：

(1)、补全条形统计图，并求D类所对应扇形的圆心角的大小；

(2)、已知D类中有2名女生，从D类中随机抽取2名同学，求抽到“一男一女”的概率.

查看试题解析
24. 如图，一次函数 $y = a x + b$ 的图象与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象分别交于点 $A (m ， 3)$ 和点 $B (6 ， 1)$ ，与y轴交于点C.

(1)、求m的值；

(2)、求直线AB的解析式；

(3)、若线段OC的垂直平分线交双曲线于点M，交直线AB于点N，求线段MN的长.

查看试题解析
25. 如图， $Rt △ A B C$ 中， $∠ A B C = 90 °$ .以AB为直径作 $⊙ O$ ，与AC相交于点D，连接BD.点E为 $⊙ O$ 上一点，且 $C E = C B$ ，连接EO并延长交CB的延长线于点F.

(1)、求证： $△ A D B ∽ △ A B C$ ；

(2)、求证：CE是 $⊙ O$ 的切线；

(3)、若 $A D \cdot A C = 36 ， B F = 4$ ，求AC的长.

查看试题解析
26. 某水果店销售某品牌苹果，该苹果每箱的进价是50元，若每箱销售80元，每星期可卖200箱.为了促销，该水果店决定降价促销.市场调查反映：若售价每降低1元，每星期可多卖出10箱.设该苹果每箱售价x元（ $50 ⩽ x ⩽ 80$ ），每星期的销售量为y箱.

(1)、求y与x之间的函数关系式；

(2)、当每箱为多少元时，每星期的销售利润达到6000元？

查看试题解析
27. 如图，在矩形ABCD中，点O是边AD的中点，点E是边BC上的一个动点，延长EO到F，使得 $O E = O F$ .

(1)、当点E运动到什么位置时，四边形AEDF是菱形？（直接写出答案）

(2)、若矩形ABCD的周长为20，求四边形AEDF的面积的最大值；

(3)、若 $A B = m$ ，且存在点E，使四边形AEDF能成为一个矩形，求BC的取值范围.

查看试题解析
28. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 6$ 与x轴交于点 $A (- 1 ， 0) ， B (3 ， 0)$ ，与y轴交于点C，点P是第一象限内抛物线上的动点.

(1)、求抛物线的解析式；

(2)、连接BC与OP，交于点D，当 $P D ： O D$ 的值最大时，求点P的坐标；

(3)、点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N使 $∠ C M N = 90 °$ ，且 $△ C M N$ 与 $△ B O C$ 相似，若存在，请直接写出点M的坐标.

查看试题解析

年龄/岁	12	13	14	15	16
人数/人	2	4	5	7	5