四川省成都市高新区2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. ﹣ 的相反数是( )A、﹣5 B、5 C、﹣ D、2. 如图是由四个完全相同的小正方体组合而成的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2021年2月24日,我国首次火星探测任务天问一号探测器成功实施第三次近火制动,进入火星停泊轨道.此次天问一号探测器进入的火星停泊轨道是与火星的最远距离59000公里的椭圆形轨道.将59000用科学记数法表示为( )A、 B、 C、 D、4. 在平面直角坐标系中,将点 向左平移2个单位长度后得到的点的坐标为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , ,则 的度数为( )
3. 2021年2月24日,我国首次火星探测任务天问一号探测器成功实施第三次近火制动,进入火星停泊轨道.此次天问一号探测器进入的火星停泊轨道是与火星的最远距离59000公里的椭圆形轨道.将59000用科学记数法表示为( )A、 B、 C、 D、4. 在平面直角坐标系中,将点 向左平移2个单位长度后得到的点的坐标为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , ,则 的度数为( )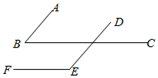 A、 B、 C、 D、7. 2021年8月18日,第三十一届世界大学生夏季运动会将在四川成都举行.为迎接大运会的到来,某校开展了主题为“爱成都•迎大运”的演讲比赛.九年级10名同学参加该演讲比赛的成绩如下表,则这组数据的众数和中位数分别为( )
A、 B、 C、 D、7. 2021年8月18日,第三十一届世界大学生夏季运动会将在四川成都举行.为迎接大运会的到来,某校开展了主题为“爱成都•迎大运”的演讲比赛.九年级10名同学参加该演讲比赛的成绩如下表,则这组数据的众数和中位数分别为( )成绩/分
80
85
90
95
人数/人
2
3
4
1
A、 85,87.5 B、85,85 C、90,85 D、90,87.58. 方程组 的解是( )A、 B、 C、 D、9. 如图,二次函数 图象的对称轴是 ,下列说法正确的是( ) A、 B、 C、 D、10. 如图,四边形 是半径为3的 的内接四边形,连接 , .若 ,则 的长为( )
A、 B、 C、 D、10. 如图,四边形 是半径为3的 的内接四边形,连接 , .若 ,则 的长为( )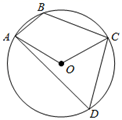 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
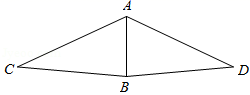
11. 因式分解: .12. 如图, , , ,则 的度数为.
 13. 一次函数 的函数值 随 值的增大而增大,则 的取值范围是.14. 如图,▱ABCD的对角线AC与BD交于点O,BD⊥AD,AB=10,AD=6,则AC的长为.
13. 一次函数 的函数值 随 值的增大而增大,则 的取值范围是.14. 如图,▱ABCD的对角线AC与BD交于点O,BD⊥AD,AB=10,AD=6,则AC的长为.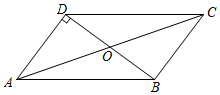 15. 若 ,则 的值为.16. 若关于 的方程 的解为正数,则 的取值范围是.17. 数学家刘徽首创割圆术,用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图,正六边形 的边长为2,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.
15. 若 ,则 的值为.16. 若关于 的方程 的解为正数,则 的取值范围是.17. 数学家刘徽首创割圆术,用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图,正六边形 的边长为2,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.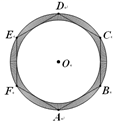 18. 如图,在矩形ABCD中,AB=9,BC=12,F是边AD上一点,连接BF,将△ABF沿BF折叠使点A落在G点,连接AG并延长交CD于点E,连接GD.若△DEG是以DG为腰的等腰三角形,则AF的长为.
18. 如图,在矩形ABCD中,AB=9,BC=12,F是边AD上一点,连接BF,将△ABF沿BF折叠使点A落在G点,连接AG并延长交CD于点E,连接GD.若△DEG是以DG为腰的等腰三角形,则AF的长为.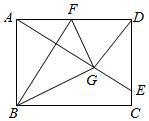 19. 如图,反比例函数 的图象与直线 交于 , 两点(点 在点 右侧),过点 作 轴的垂线,垂足为点 ,连接 , ,图中阴影部分的面积为12,则 的值为.
19. 如图,反比例函数 的图象与直线 交于 , 两点(点 在点 右侧),过点 作 轴的垂线,垂足为点 ,连接 , ,图中阴影部分的面积为12,则 的值为.
三、解答题
-
20.(1)、计算: +sin30°+| ﹣2|;(2)、解不等式组: .21. 先化简,再求值: ,从﹣2,﹣1,2中选取一个合适的数作为a的值代入求值.22. 为帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志,某校开展了“一人一球”的体育选修课活动.学生根据自己的喜好选择一门球类项目( :篮球, :足球, :排球, :羽毛球, :乒乓球),王老师随机对该校部分学生的选课情况进行调查后;制成了两幅不完整的统计图(如图所示).
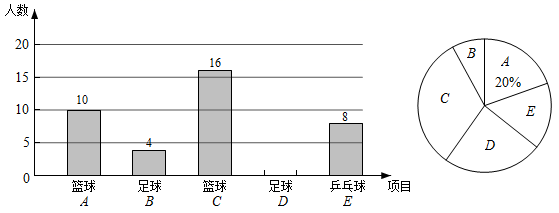 (1)、王老师调查的学生人数是 ▲ ,请将条形统计图补充完整;(2)、若该校共有学生1500名,请估计有多少学生选修乒乓球?(3)、现有4名学生,2人选修篮球,1人选修足球,1人选修排球,王老师要从这4人中任选2人了解他们对体育选修课的看法,请用列表或画树状图的方法,求出所选2人都是选修篮球的概率.23. 如图,一艘货轮以40海里/小时的速度在海面上航行,当它行驶到 处时,发现它的东北方向有一灯塔 ,货轮继续向北航行30分钟后到达 点,发现灯塔 在它北偏东 方向,求此时货轮与灯塔 的距离.(结果精确到0.1海里,参考数据: , )
(1)、王老师调查的学生人数是 ▲ ,请将条形统计图补充完整;(2)、若该校共有学生1500名,请估计有多少学生选修乒乓球?(3)、现有4名学生,2人选修篮球,1人选修足球,1人选修排球,王老师要从这4人中任选2人了解他们对体育选修课的看法,请用列表或画树状图的方法,求出所选2人都是选修篮球的概率.23. 如图,一艘货轮以40海里/小时的速度在海面上航行,当它行驶到 处时,发现它的东北方向有一灯塔 ,货轮继续向北航行30分钟后到达 点,发现灯塔 在它北偏东 方向,求此时货轮与灯塔 的距离.(结果精确到0.1海里,参考数据: , )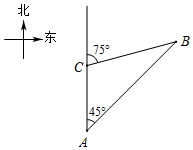 24. 如图,在平面直角坐标系 中,直线 与反比例函数 的图象交于点 ,点 的横坐标为4.
24. 如图,在平面直角坐标系 中,直线 与反比例函数 的图象交于点 ,点 的横坐标为4.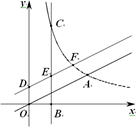 (1)、求反比例函数的表达式;(2)、过点 作 轴的垂线,与反比例函数图象交于点 ,将直线 向上平移 个单位长度后与 轴交于点 ,与直线 交于点 ,与反比例函数图象交于点 .若 ,求 的值.25. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)、求反比例函数的表达式;(2)、过点 作 轴的垂线,与反比例函数图象交于点 ,将直线 向上平移 个单位长度后与 轴交于点 ,与直线 交于点 ,与反比例函数图象交于点 .若 ,求 的值.25. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.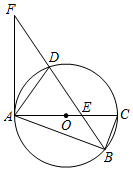 (1)、求证:AF为⊙O的切线;(2)、当点D为EF的中点时,求证:AD2=AO•AE;(3)、在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.26. 2021年春节,不少市民响应国家号召原地过年.为保障市民节日消费需求,某商家宣布“今年春节不打烊”,该商家以每件80元的价格购进一批商品,规定每件商品的售价不低于进价且不高于100元,经市场调查发现,该批商品的日销售量 (件)与每件售价 (元)满足一次函数关系,其部分对应数据如下表所示:
(1)、求证:AF为⊙O的切线;(2)、当点D为EF的中点时,求证:AD2=AO•AE;(3)、在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.26. 2021年春节,不少市民响应国家号召原地过年.为保障市民节日消费需求,某商家宣布“今年春节不打烊”,该商家以每件80元的价格购进一批商品,规定每件商品的售价不低于进价且不高于100元,经市场调查发现,该批商品的日销售量 (件)与每件售价 (元)满足一次函数关系,其部分对应数据如下表所示:每件售价 (元)
…
85
90
95
…
日销售量 (件)
…
230
180
130
…
(1)、求 与 之间的函数关系式;(2)、当每件商品的售价定为多少元时,该批商品的日销售利润最大?日销售最大利润是多少?27. 如图1,在Rt△ABC中,∠ABC=90°,D,E分别为边BC,AC上的点,连接DE,过D作DF⊥DE交AC边于点F(F不与点C重合),点G为射线DF上一点,连接EG,使∠BAC=∠DEG=α.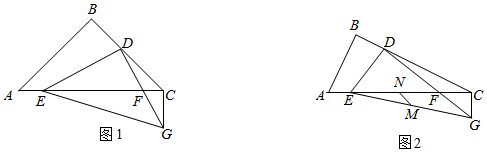 (1)、连接CG,求证:△DEF∽△CGF;(2)、当α=45°时,请探究AE,BD与CG三者满足的数量关系,并证明;(3)、如图2,点M,N分别为EG和AC的中点,连接MN.若tanα=2,BD= CD,AC=10,请直接写出MN的最小值.28. 抛物线y=﹣x2+mx+2n(m,n为常数,且n>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点 C.
(1)、连接CG,求证:△DEF∽△CGF;(2)、当α=45°时,请探究AE,BD与CG三者满足的数量关系,并证明;(3)、如图2,点M,N分别为EG和AC的中点,连接MN.若tanα=2,BD= CD,AC=10,请直接写出MN的最小值.28. 抛物线y=﹣x2+mx+2n(m,n为常数,且n>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点 C. (1)、若点B的横坐标为4,抛物线的对称轴为x= .
(1)、若点B的横坐标为4,抛物线的对称轴为x= .ⅰ)求该抛物线的函数表达式;
ⅱ)如图1,在直线BC上方的抛物线上取点D,连接AD,交BC于点E,若 =7,求点D的坐标.
(2)、如图2,当m=n﹣2时,过点A作BC的平行线,与y轴交于点F,将抛物线在直线BC上方的图象沿BC折叠,若折叠后的图象(图中虚线部分)与直线AF有且只有一个公共点,求n的值.