陕西省咸阳市兴平市2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
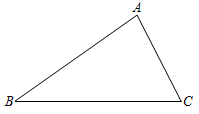
1. 计算的结果是( )A、-2 B、2 C、-8 D、82. 如图是某个几何体的三视图,该几何体是( )
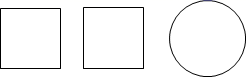
主视图 左视图 俯视图
A、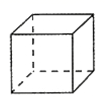 B、
B、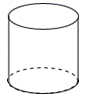 C、
C、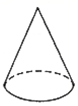 D、
D、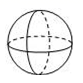 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )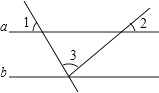 A、40° B、60° C、80° D、100°5. 已知一次函数 ,y 的值随 x 值的增大而减小, 点在该一次函数的图象上,则 n 的取值范围为( )A、 B、 C、 D、6. 如图,CM 是 的中线, 的周长比 的周长大 , ,则 AC 的长为( )
A、40° B、60° C、80° D、100°5. 已知一次函数 ,y 的值随 x 值的增大而减小, 点在该一次函数的图象上,则 n 的取值范围为( )A、 B、 C、 D、6. 如图,CM 是 的中线, 的周长比 的周长大 , ,则 AC 的长为( )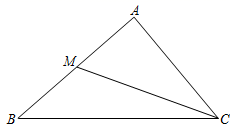 A、 B、 C、 D、7.
A、 B、 C、 D、7.如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
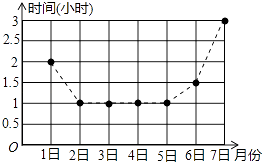 A、1小时 B、1.5小时 C、2小时 D、3小时8. 如图,在矩形 中, , ,点 E 在边 上,且 .连接 ,将 沿 折叠,点 C 的对应点 恰好落在边 上,则 ( )
A、1小时 B、1.5小时 C、2小时 D、3小时8. 如图,在矩形 中, , ,点 E 在边 上,且 .连接 ,将 沿 折叠,点 C 的对应点 恰好落在边 上,则 ( )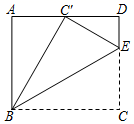 A、 B、 C、 D、59. 如图, 是 的内接三角形,且 , , 的直径 交 于点E,则 的度数为( )
A、 B、 C、 D、59. 如图, 是 的内接三角形,且 , , 的直径 交 于点E,则 的度数为( )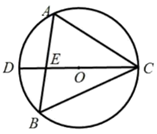 A、 B、 C、 D、10. 在平面直角坐标系中,将抛物线y=﹣x2+(m﹣1)x+m绕原点旋转180°,在旋转后的抛物线上,当x 4时,y随x的增大而增大,则m的范围是( )A、m ﹣7 B、m ﹣7 C、m ﹣7 D、m ﹣7
A、 B、 C、 D、10. 在平面直角坐标系中,将抛物线y=﹣x2+(m﹣1)x+m绕原点旋转180°,在旋转后的抛物线上,当x 4时,y随x的增大而增大,则m的范围是( )A、m ﹣7 B、m ﹣7 C、m ﹣7 D、m ﹣7二、填空题
-
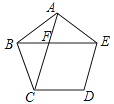
11. 不等式 的解集为.12. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .
 13. 如图,在平面直角坐标系中,一条过原点的直线与反比例函数 的图象相交于 两点,若 , ,则该反比例函数的表达式为.
13. 如图,在平面直角坐标系中,一条过原点的直线与反比例函数 的图象相交于 两点,若 , ,则该反比例函数的表达式为.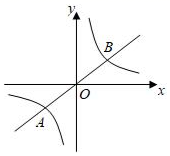 14. 已知矩形 , , ,点 E 为 边的中点,点 F 为 边上的动点,点 B 和点 关于 对称,则 的最小值是.
14. 已知矩形 , , ,点 E 为 边的中点,点 F 为 边上的动点,点 B 和点 关于 对称,则 的最小值是.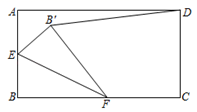
三、解答题
-
15. 计算:16. 化简:17. 如图,请用尺规作 ,使得 与 BC 相切(不写作法,保留作图痕迹)
 18. 如图,在 中, , 平分 ,交 于点 D,过点 D 作 于点 E.
18. 如图,在 中, , 平分 ,交 于点 D,过点 D 作 于点 E.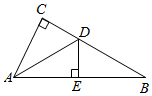 (1)、求证: ;(2)、若 , ,求 的长.19. 西安市统一体育考试时间定为 5 月 3 日至 6 月 29 日进行,某校课题研究小组对本校九年整全体同学体有测试情况进行调在他们质机抽责部分同学体方测试成绩(由高到低分A、B、C、D 四个等级),根据调查的数据绘制成如图不完整的条形统计图和扇形统计图.请解答下列问题:
(1)、求证: ;(2)、若 , ,求 的长.19. 西安市统一体育考试时间定为 5 月 3 日至 6 月 29 日进行,某校课题研究小组对本校九年整全体同学体有测试情况进行调在他们质机抽责部分同学体方测试成绩(由高到低分A、B、C、D 四个等级),根据调查的数据绘制成如图不完整的条形统计图和扇形统计图.请解答下列问题: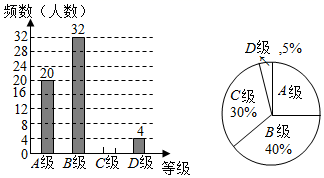 (1)、该课题研究小组共抽查了 ▲ 名同学的体育测试成绩,请补全条形统计图;(2)、这些同学的体育测试成绩的中位数落在级,扇形统计图中 A 级所占的百分比为;(3)、若该校九年级共有800名同学,请估计该校九年级同学体育测试约有多少人达标.(测试成绩C 级以上,含 C 级)20. 如图所示,某校综合实践活动小组的同学欲测量公园内一棵树 的高度,他们在这棵树的正前方一座楼亭前的台阶上 点处测得树顶端 的仰角为 ,朝着这棵树的方向走到台阶下的点 处,测得树顶端 的仰角为 .已知 点的高度 为3米,台阶 的坡比为1: (即AB:BC=1: ),且 、 、 三点在同一条直线上.请根据以上条件求出树 的高度(侧倾器的高度忽略不计).
(1)、该课题研究小组共抽查了 ▲ 名同学的体育测试成绩,请补全条形统计图;(2)、这些同学的体育测试成绩的中位数落在级,扇形统计图中 A 级所占的百分比为;(3)、若该校九年级共有800名同学,请估计该校九年级同学体育测试约有多少人达标.(测试成绩C 级以上,含 C 级)20. 如图所示,某校综合实践活动小组的同学欲测量公园内一棵树 的高度,他们在这棵树的正前方一座楼亭前的台阶上 点处测得树顶端 的仰角为 ,朝着这棵树的方向走到台阶下的点 处,测得树顶端 的仰角为 .已知 点的高度 为3米,台阶 的坡比为1: (即AB:BC=1: ),且 、 、 三点在同一条直线上.请根据以上条件求出树 的高度(侧倾器的高度忽略不计).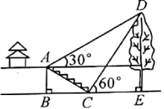 21. 为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.(1)、以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;(2)、若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?22. 第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.(1)、若从这20人中随机选取一人作为联络员,求选到女生的概率;(2)、若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.23. 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
21. 为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.(1)、以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;(2)、若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?22. 第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.(1)、若从这20人中随机选取一人作为联络员,求选到女生的概率;(2)、若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.23. 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.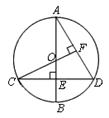 (1)、证明:点E是OB的中点;(2)、若AB=8,求CD的长.24. 如图,抛物线 与y轴交于点 ,与x轴交于B、C两点,且抛物线的对称轴方程为 .
(1)、证明:点E是OB的中点;(2)、若AB=8,求CD的长.24. 如图,抛物线 与y轴交于点 ,与x轴交于B、C两点,且抛物线的对称轴方程为 .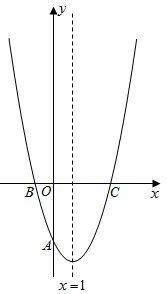 (1)、求抛物线的解析式;(2)、设点P为抛物线对称轴上第一象限内一点,若 的面积为4,求点P的坐标;(3)、点M为抛物线上一点,点N为抛物线的对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时( 为平行四边形的一条边),求此时点M的坐标.25. 如图
(1)、求抛物线的解析式;(2)、设点P为抛物线对称轴上第一象限内一点,若 的面积为4,求点P的坐标;(3)、点M为抛物线上一点,点N为抛物线的对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时( 为平行四边形的一条边),求此时点M的坐标.25. 如图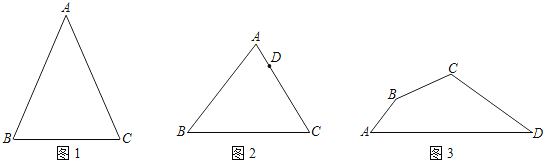 (1)、问题提出:
(1)、问题提出:如图1,在△ABC中,已知AB=AC=5,BC=4,在BC上找一点D,使得线段AD将△ABC分成面积相等的两部分,画出线段AD,并写出AD的长为 ▲ .
(2)、问题探究:如图2,点D是△ABC边AC上一定点,在BC上找一点E,使得线段DE将△ABC分成面积相等的两部分,并说明理由.
(3)、问题解决:如图3,四边形ABCD是西安市高新区新近改造过程中的一块不规则空地,为了美化环境,市规划办决定在这块地里种植两种花卉,打算过点C修一条笔直的通道,以便市民出行观赏花卉,要求通道两侧种植花卉的面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长.