宁夏银川市贺兰县2021年数学中考模拟试卷（一）

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算，错误的是（）.

A、 ${(a^{2})}^{3} = a^{6}$ B、 ${(x + y)}^{2} = x^{2} + y^{2}$ C、 ${(\sqrt{5} - 1)}^{0} = 1$ D、61200 = 6.12×10 ⁴

查看试题解析
2. 未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（　　）

A、0.845×10⁴亿元 B、8.45×10³亿元 C、8.45×10⁴亿元 D、84.5×10²亿元

查看试题解析
3. 如图所示，直线l经过第二，三，四象限，l的解析式是 $y = (m - 2) x + n$ ，则m的取值范围则数轴上表示为（）

A、 B、 C、 D、

查看试题解析
4. 菱形ABCD的一条对角线长为6，边AB的长为方程y²﹣7y+10=0的一个根，则菱形ABCD的周长为（　　）

A、8 B、20 C、8或20 D、10

查看试题解析
5. 如图是根据某班40名同学一周的体育锻炼情况绘制的统计图，该班40名同学一周参加体育锻炼时间的中位数，众数分别是（）

A、10.5，16 B、8.5，16 C、8.5，8 D、9，8

查看试题解析
6. 如图，在△ABC中，∠CAB＝70°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）

A、35° B、40° C、50° D、70°

查看试题解析
7. 如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E.过半圆上一点F作半圆的切线，分别交AB，AC于M，N.那么 $\frac{B M \cdot C N}{B C^{2}}$ 的值等于（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、1

查看试题解析
8. 已知二次函数 $y = - \frac{1}{4} x^{2} + b x + c$ 的图象如下，则一次函数 $y = - \frac{1}{4} x - 2 b$ 与反比例函数 $y = \frac{c}{x}$ 在同一平面直角坐标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 分解因式3x²﹣27y²＝.

查看试题解析
10. 某校举行“中国诗词大会”的比赛每班限报一名选手，九（1）班甲、乙、丙、丁四位选手在班级选拔赛时的数据如表：

甲

乙

丙

丁

平均分

9.8

9.3

9.2

9.8

方差

1.5

3.2

3.3

6.8

根据表中数据，要从四个同学中选择一个成绩好且发挥稳定的参加比赛，应该选择是（填“甲”或“乙”或“丙”或“丁”）

查看试题解析
11. 计算：( $\frac{1}{3}$ )^-1－|－2＋ $\sqrt{3}$ tan45°|＋( $\sqrt{2}$ －1.41)⁰＝.

查看试题解析
12. 如图，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时，竹竿与这一点相距8m、与旗杆相距22m，则旗杆的高为.

查看试题解析
13. 如果在解关于x的分式方程 $\frac{x}{x - 1} + \frac{k}{1 - x} = 2$ 时出现了增根x＝1，那么常数k的值为.

查看试题解析
14. 如图是一个几何体的三视图（图中尺寸单位： $c m$ ），根据图中数据计算，这个几何体的表面积为 $c m^{2}$ ．

查看试题解析
15.
如图，为保护门源百里油菜花海，由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB，AC．若∠B=56°，∠C=45°，则游客中心A到观景长廊BC的距离AD的长约为米．（sin56°≈0.8，tan56°≈1.5）

查看试题解析
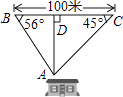16. 二次函数y＝ax²+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b²；③2a+b＞0；④其顶点坐标为（ $\frac{1}{2}$ ，﹣2）；⑤当x＜ $\frac{1}{2}$ 时，y随x的增大而减小；⑥a+b+c＞0中，正确的有.（只填序号）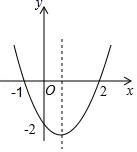

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} x - 4 \leq \frac{3}{2} (2 x - 1) \\ 2 x - \frac{1 + 3 x}{2} < 1 \end{matrix}$ ，把解集表示在数轴上，并求出不等式组的整数解.

查看试题解析
18. 先化简，再求值： $\frac{1}{x + 2} - \frac{x + 3}{x^{2} - 4} \div \frac{x^{2} + 5 x + 6}{{(x - 2)}^{2}}$ ，其中 $x = \sqrt{3} - 2$ .

查看试题解析
19. 已知△ABC在平面直角坐标系内，三个顶点的坐标分别为A(0，3)，B(4，5)，C(3，2)．(正方形网格中，每个小正方形的边长都是1个单位长度)

(1)、画出△ABC向下平移5个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ，并直接写出点 $C_{1}$ 的坐标；

(2)、以点B为位似中心，在网格中画出 $△ A_{2} B C_{2}$ ，使 $△ A_{2} B C_{2}$ 与 $△ A B C$ 位似，且相似比为2∶1，并直接写出 $△ A_{2} B C_{2}$ 的面积．

查看试题解析
20. 为落实疫情期间的垃圾分类，树立全面环保意识，某校举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为 $A$ ， $B$ ， $C$ ， $D$ 四个等级，并绘制了不完整的两种统计图：

根据图中提供的信息，回答下列问题：

(1)、参加知识竞赛的学生共有人，并把条形统计图补充完整；

(2)、扇形统计图中， $m =$ ， $n =$ ， $C$ 等级对应的圆心角为度；

(3)、小明是四名获 $A$ 等级的学生中的一位，学校将从获 $A$ 等级的学生中任选取2人，参加市举办的知识竞赛，请用列表法或画树状图，求小明被选中参加区知识竞赛的概率.

查看试题解析
21. 如图，在▱ABCD中，E，F分别为边AB，CD的中点，BD是对角线．

(1)、求证：△ADE≌△CBF；

(2)、若∠ADB是直角，请证明四边形BEDF是菱形．

查看试题解析
22. 4月20日8时2分，四川省雅安市芦山县发生了7.0级地震，当地的部分房屋严重受损，上万灾民无家可归，灾情牵动亿万中国人的心．某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地，若用大、小两种货车共20辆，恰好能一次性运完这批物资．已知这两种货车的载重量分别为16吨/辆和10吨/辆，运往甲、乙两地的运费如下表：
车型
运往地
甲地（元/辆）
乙地（元/辆）
大货车
720
800
小货车
500
650

(1)、求这两种货车各用多少辆？

(2)、如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，前往甲、乙两地的总运费为w元，求出w与a的函数关系式（写出自变量的取值范围）；

(3)、在（2）的条件下，若运往甲地的物资不少于132吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费．

查看试题解析
23. 如图△ABC内接于⊙O ， $∠ A C B = 60 °$ ，BD是⊙O的直径，点P是BD延长线上一点，且PA是⊙O的切线．

(1)、求证： $A P = A B$ ；

(2)、若 $P D = \sqrt{5}$ ，求⊙O的直径．

查看试题解析
24. 如图一次函数y＝k₁x+3的图象与坐标轴相交于点A（﹣2，0）和点B，与反比例函数y＝ $\frac{k_{2}}{x}$ （x＞0）相交于点C（2，m）.

(1)、求出一次函数与反比例函数的解析式；

(2)、若点P是反比例函数图象上的一点，连接CP并延长，交x轴正半轴于点D，若PD：CP＝1：2时，求△COP的面积.

查看试题解析
25. 随着《流浪地球》的热播，其同名科幻小说的销量也急剧上升.为应对这种变化，某网店分别花20000元和30000元先后两次增购该小说，第二次的数量比第一次多500套，且两次进价相同.

(1)、该科幻小说第一次购进多少套？

(2)、根据以往经验：当销售单价是25元时，每天的销售量是250套；销售单价每上涨1元，每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y（套）与销售单价x（元）之间的函数关系式及自变量x的取值范围；

②网店决定每销售1套该科幻小说，就捐赠a（0＜a＜7）元给困难职工，每天扣除捐赠后可获得的最大利润为1960元，求a的值.

查看试题解析
26. 综合与探究
如图，抛物线 $y = \frac{1}{4} x^{2} - \frac{1}{2} x - 2$ ，与x轴交于A ， B两点(点A在点B的左侧)，与y轴交于点C ，抛物线的对称轴为l ．

(1)、求点A ， B ， C的坐标；

(2)、若点D是第一象限内抛物线上一点，过点D作 $D E ⊥ x$ 轴于点E ，交直线BC于点F ，当 $O E = 4 D F$ 时，求四边形DOBF的面积；

(3)、在（2）的条件下，若点M在抛物线上，点N在抛物线的对称轴上，是否存在以点B ， D ， M ， N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

查看试题解析

	甲	乙	丙	丁
平均分	9.8	9.3	9.2	9.8
方差	1.5	3.2	3.3	6.8