江苏省扬州市江都区八校2021年数学中考模拟联考试卷（3月）

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列运算正确的是（）

A、 $a^{6} \div a^{3} = a^{3}$ B、 ${(a^{3})}^{3} = a^{6}$ C、 $a^{3} \cdot a^{2} = a^{6}$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
3. 函数y＝ $\sqrt{2 - x}$ 中自变量x的取值范围是（）

A、x＞2 B、x≤2 C、x≥2 D、x≠2

查看试题解析
4. 如图所示几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 一组数据为x，2，4，10，14，8.若这组数据的众数为10，则这组数据的中位数为（）

A、7 B、8 C、9 D、10

查看试题解析
6. 如图，△ABC内接于⊙O，∠OBC＝40°，则∠A的度数为（）

A、80° B、100° C、110° D、130°

查看试题解析
7. 如图，把正方形纸片 $A B C D$ 沿对边中点所在的直线对折后展开，折痕为MN，再过点C折叠纸片，使点C落在MN上的点F处，折痕为BE.若AB的长为1，则FM的长为（）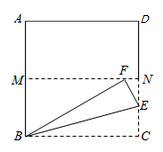

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
8. 关于x的一元二次方程 $x^{2} - 2 x - t = 0$ （t为实数）有且只有一个根在 $- 2 < x < 3$ 的范围内，则t的取值范围是（）

A、 $3 \leq t < 8$ B、 $- 1 \leq t < 8$ C、 $3 \leq t < 8$ 或 $t = - 1$ D、 $- 1 < t < 3$

查看试题解析

二、填空题

9. 因式分解： $a^{3} - a =$ ．

查看试题解析
10. 如果正比例函数 $y = (k - 1) x$ 的图象经过原点和第一、第三象限，那么 $k$ .

查看试题解析
11. 如图，将三角尺的直角顶点放在直尺的一边上， $∠ 1 = 30 °$ ， $∠ 3 = 35 °$ ，则 $∠ 2$ 的度数为 $°$ .

查看试题解析
12. 如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是.

查看试题解析
13. 已知圆锥的底面半径为3cm，母线长为5cm，则这个圆锥的侧面积是cm².

查看试题解析
14. 如图，正方形网格中，每个正方形边长都相等，A、O、B在如图的格点上，则 $\sin ∠ A O B =$ .

查看试题解析
15. a、b是一元二次方程 $x^{2} - x - 3 = 0$ 的两根，则 $a^{2} - 2 a - b$ 值为.

查看试题解析
16. 如图，点A在双曲线y= $\frac{3}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，过点A作AD⊥x轴于D，连接OB，与AD相交于点C，若AC=2CD，则k的值为．

查看试题解析
17. 如图，将矩形 $O A B C$ 置于平面直角坐标系中，B点坐标为 $(10 ， 7)$ ，点D为BC上一点，且 $D C = 2$ ，连接AD，将 $△ A B D$ 沿AD折叠，压平，使B点的对应点E落在坐标平面内.若抛物线 $y = a x^{2} - 8 a x + 10$ （ $a \neq 0$ ，a为常数）的顶点落在 $△ A D E$ 的内部（不含边界），则a的取值范围为.

查看试题解析

三、解答题

18. 计算：

(1)、 $- \sqrt{27} + | \sqrt{3} - 2 | - {(- \frac{1}{3})}^{- 1} + 2 \cos 30 °$ ；

(2)、 $(\frac{1}{x - 2} + 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ .

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 (x + 2) < 3 x + 3 \\ \frac{x - 2}{4} > \frac{x}{3} - 1 \end{array}$ ，并求出最大整数解.

查看试题解析
20. 在2017年“KFC”篮球赛进校园活动中，某校甲、乙两队进行决赛，比赛规则规定：两队之间进行3局比赛，3局比赛必须全部打完，只要赢满2局的队为获胜队，假如甲、乙两队之间每局比赛输赢的机会相同，且乙队已经赢得了第1局比赛，那么甲队获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）

查看试题解析
21. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图.请根据相关信息，解答下列问题：

(1)、扇形统计图中，初赛成绩为1.65m所在扇形图形的圆心角为_°；

(2)、补全条形统计图；

(3)、这组初赛成绩的中位数是m；

(4)、根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？

查看试题解析
22. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．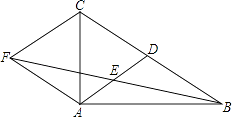

(1)、求证：AF=DC；

(2)、若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
23. 2020年12月11日，连淮扬镇高铁全线通车.某工程队承担了该道路1800米长的建造任务.工程队在建造完720米道路后，引进了新设备，每天的工作效率比原来提高了20%，结果共用27天完成了任务，问引进新设备前工程队每天建造道路多少米？

查看试题解析
24. 如图，AB是⊙O的直径，C 是⊙O上一点，过点C 作⊙O的切线，交BA的延长线交于点D，过点B 作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC.

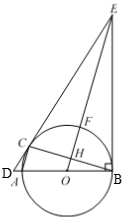(1)、求证：∠ECB=∠EBC；

(2)、连接BF，CF，若BF=5，sin∠FBC= $\frac{3}{5}$ ，求AC的长.

查看试题解析
25. 某商场经营某种品牌的玩具，购进时的单价是40元，根据市场调查：在一段时间内，销售单价是50元时，销售量是600件，而销售单价每涨2元，就会少售出20件玩具.

(1)、不妨设该种品牌玩具的销售单价为x元（x＞50），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元，并把结果填写在表格中：

销售单价（元）

x

销售量y（件）

销售玩具获得利润ω（元）

(2)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于54元，且商场要完成不少于400件的销售任务，求商场销售该品牌玩具获得的最大利润是多少元？

查看试题解析
26.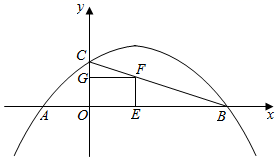 已经二次函数 $y = a x^{2} + b x + 1$ .

(1)、如图，其图象与x轴交于点 $A (- 1 ， 0)$ 和点B，与y轴交于点C，对称轴为直线 $x = 1$ .
①求二次函数解析式；

②F为线段BC上一点，过F分别作x轴，y轴垂线，垂足分别为E、F，当四边形 $O E F G$ 为正方形时，求点F坐标；

(2)、其图象上仅有一个点的横坐标、纵坐标互为相反数，且二次函数 $y = a x^{2} + b x + 1$ 函数值存在负数，求b的取值范围.

查看试题解析
27. 平面上两点间距离公式是解析几何中重要的公式之一，如图所示， $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ ，则 $P_{1} P_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ .请用所学知识解决问题：

已知道 $⊙ O$ 半径为3，

(1)、如图1， $P (x ， y)$ 为圆上任意一点，请探究x，y的关系式；

(2)、如图2，已知 $Q (a ， b)$ ，QA为 $⊙ O$ 切线， $B (2 ， - 1)$ ，且 $Q A = Q B$ ，求b关于a的函数关系式；

(3)、如图3，M点坐标 $(- 5 ， 0)$ ，在x轴上是否存在点N（不同于点M），满足对于 $⊙ O$ 上任意一点P，都有 $\frac{P N}{P M}$ 为一常数，若存在求出N点坐标，若不存在请说明理由.

查看试题解析

销售单价（元）	x
销售量y（件）
销售玩具获得利润ω（元）