江苏省盐城市建湖县2021年数学中考模拟试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的相反数是（）

A、 3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下面立体图形中，从正面、侧面、上面看，都不能看到长方形的是（）

A、长方体 B、圆柱 C、圆锥 D、正四棱锥

查看试题解析
3. 化简 $| \sqrt{2} - 3 |$ 的结果正确的是（）

A、 $\sqrt{2} - 3$ B、 $- \sqrt{2} - 3$ C、 $\sqrt{2} + 3$ D、 $3 - \sqrt{2}$

查看试题解析
4. 如图，在四边形 $A B C D$ 中， $∠ A = ∠ B D C = 90 °$ ， $∠ C = ∠ A D B$ ，点P是 $B C$ 边上的一动点，连接 $D P$ ，若 $A D = 3$ ，则DP的长不可能是（）

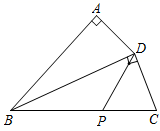A、2 B、3 C、4 D、5

查看试题解析
5. 据统计，某城市去年接待旅游人数约为89000000人，89000000这个数据用科学记数法表示为（）

A、 $8.9 \times 10^{5}$ B、 $8.9 \times 10^{6}$ C、 $8.9 \times 10^{7}$ D、 $8.9 \times 10^{8}$

查看试题解析
6. 若平行四边形两个内角的度数比为1：2，则其中较大内角的度数为（）

A、100° B、110° C、120° D、135°

查看试题解析
7. 如图，点A为反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上的一点，过点A作 $A B ⊥ y$ 轴于点B，点C为x轴上的一个动点， $△ A B C$ 的面积为3，则 k的值为（）

A、3 B、6 C、9 D、12

查看试题解析
8. 从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示.下列结论：①小球抛出3秒时达到最高点；②小球从抛出到落地经过的路程是80m；③小球的高度h＝20时，t＝1s或5s.④小球抛出2秒后的高度是35m.其中正确的有（）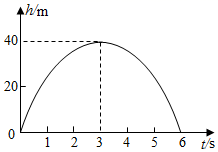

A、①② B、②③ C、①③④ D、①②③

查看试题解析

二、填空题

9. 若代数式 $\frac{1}{1 - x}$ 有意义，则实数x的取值范围是.

查看试题解析
10. 因式分解： $x^{2} - 6 x y + 9 y^{2} =$ .

查看试题解析
11. 一组从小到大排列的数据：2，5，x，y，2x，11的平均数与中位数都是7，则x-y=.

查看试题解析
12. 已知 $x = 3$ 是关于 $x$ 的方程 $a x + 2 x - 3 = 0$ 的解，则 $a$ 的值为.

查看试题解析
13. 如图，在△ABC中，M是BC边上的中点，AP是∠BAC的平分线，BP⊥AP于点P，已知AB＝16，AC＝24，那么PM的长为.

查看试题解析
14. 已知关于x，y的方程组 ${\begin{array}{l} x - y = 2 k \\ x + 3 y = 1 - 5 k \end{array}$ 的解满足不等式﹣3≤x+y≤1，则实数k的取值范围为.

查看试题解析
15. 菱形 $O A B C$ 在平面直角坐标系中的位置如图所示， $∠ A O C = 60^{\circ}$ ， $O C = \sqrt{3}$ ，则点 $B$ 的坐标为.

查看试题解析
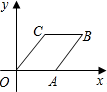16. 在平面直角坐标系中，直线y＝﹣x+6分别与x轴、y轴交于点A、B两点，点C在y轴左边，且∠ACB＝90°，则点C的横坐标x_c的取值范围是.

查看试题解析

三、解答题

17. 计算：（π﹣3020）⁰﹣2cos45°﹣ $\sqrt{27}$ +|1﹣ $\sqrt{3}$ |.

查看试题解析
18. 解方程： $\frac{2 x}{x - 2} - \frac{1}{2 - x} = 1$

查看试题解析
19. 先化简，再求值：

(1)、6x²y（﹣2xy＋y³）÷xy² ，其中x＝2，y＝﹣1；

(2)、（x＋2y）（x﹣2y）＋（x﹣2y）²﹣（6x²y﹣2xy²）÷（2y），其中x＝﹣2，y＝ $\frac{1}{2}$ .

查看试题解析
20. 如图，BD是△ABC的角平分线，点E、F分别在BC、AB上，且DE∥AB，EF∥AC；

(1)、求证：BE＝AF；

(2)、如图，若∠A＝∠C＝60°，请写出4个面积等于△ABC面积一半的几何图形.

查看试题解析
21. 图中圆形转盘被均分成面积相等的四等份，小明和小亮用其做游戏：分别转动转盘两次，若两次数字之和为偶数则小明胜，若数字之和为奇数则小亮胜，你认为游戏是否公平？请说明理由.

查看试题解析
22. 某学校为了丰富学生课余生活，开展了“第二课堂”活动，推出了以下四种选修课程： $A$ .绘画； $B$ .唱歌； $C$ .跳舞； $D$ .演讲； $E$ .书法.学校规定：每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制了如下两幅不完整的统计图.

请结合统计图中的信息解决下列问题：

(1)、这次抽查的学生人数是多少人？

(2)、将条形统计图补充完整.

(3)、求扇形统计图中课程 $E$ 所对应扇形的圆心角的度数.

(4)、如果该校共有1200名学生，请你估计该校选择课程 $D$ 的学生约有多少人.

查看试题解析
23. 如图，四边形ABCD内接于⊙O ， ∠BAD=90°，AD、BC的延长线交于点F ，点E在CF上，且∠DEC=∠BAC ．

(1)、求证：DE是⊙O的切线；

(2)、若AB=AC ， CE=10，EF=14，求CD ．

查看试题解析
24. 某校为改善教师的办公环境，计划购进A，B两种办公椅共100把.经市场调查：购买A种办公椅2把，B种办公椅5把，共需600元；购买A种办公椅3把，B种办公椅1把，共需380元.

(1)、求A种，B种办公椅每把各多少元？

(2)、因实际需要，购买A种办公椅的数量不少于B种办公椅数量的3倍.学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其它因素），实际付款总金额按市场价九折优惠.请设计一种购买办公椅的方案，使实际所花费用最省，并求出最省的费用.

查看试题解析
25. 元旦期间，小黄自驾游去了离家156千米的黄石矿博园，右图是小黄离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．

(1)、求小黄出发0.5小时时，离家的距离；

(2)、求出AB段的图象的函数解析式；

(3)、小黄出发1.5小时时，离目的地还有多少千米？

查看试题解析
26. 在平行四边形ABCD中，点E、F分别在边AB、BC上，DE、AF交于点M.

(1)、如图1，E为AB的中点，AF⊥BC交BC于点F，过点E作EN⊥AF交AF于点N， $\frac{B F}{A D} = \frac{1}{3}$ ，直接写出 $\frac{M N}{A M}$ 的值是；

(2)、如图2，∠B＝90°，∠ADE＝∠BAF，求证：△AEM∽△AFB；

(3)、如图3，∠B＝60°，AB＝AD，∠ADE＝∠BAF，求证： $\frac{BF}{CF} = \frac{A E}{A D}$ .

查看试题解析