江苏省盐城市东台市第五教育联盟2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. ﹣ 的倒数是( )A、﹣ B、 C、﹣3 D、32. 下列标志是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,是由5个大小相同的小正方体摆成的几何体,从上面看到的平面图形是( )
3. 如图,是由5个大小相同的小正方体摆成的几何体,从上面看到的平面图形是( )
 A、
A、 B、
B、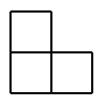 C、
C、 D、
D、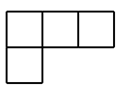 4. 下列计算正确的是( )A、 B、 C、 D、5. 2019年10月1日国庆阅兵式上首次亮相了我国自主研发的洲际导弹导弹“东风41号”,它的射程可以达到12000公里,数据12000用科学记数法表示为( )A、1.2×103 B、1.2×104 C、12×103 D、12×1046. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 2019年10月1日国庆阅兵式上首次亮相了我国自主研发的洲际导弹导弹“东风41号”,它的射程可以达到12000公里,数据12000用科学记数法表示为( )A、1.2×103 B、1.2×104 C、12×103 D、12×1046. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )年龄(岁)
14
15
16
17
18
人数(人)
1
4
3
2
2
A、15,16 B、15,15 C、15,15.5 D、16,157. 一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于( )A、36 πcm2 B、24πcm2 C、18πcm2 D、12 πcm28. 已知α,β是方程x2+2017x+1=0的两个根,则(1+2019α+α2)(1+2019β+β2)的值为( )A、1 B、2 C、3 D、4二、填空题
-
9. 一组数1、2、3、4、5的方差是 与另一组数3、4、5、6、7的方差 的大小比较 (填写:大于、等于、小于).10. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 11. 分解因式: .12. 若 在实数范围内有意义,则x的取值范围为 .13. 抛物线 的顶点坐标是.14. 抛物线经过坐标系(-1,0)和(0,3)两点,对称轴 ,如图所示,则当 时,x的取值范围是.
11. 分解因式: .12. 若 在实数范围内有意义,则x的取值范围为 .13. 抛物线 的顶点坐标是.14. 抛物线经过坐标系(-1,0)和(0,3)两点,对称轴 ,如图所示,则当 时,x的取值范围是. 15. 如图,四边形 内接于 , 是 的直径, , 与 相交于点 ,若 ,则 .
15. 如图,四边形 内接于 , 是 的直径, , 与 相交于点 ,若 ,则 . 16. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是.
16. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是.
三、解答题
-
17. 计算:18. 解分式方程: +1= .19. 先化简,再求值: ,其中 .20. 小涵和小悦商定来玩一种“摸字组词”游戏.一个不透明的口袋里装有分别标有 “奋”“发”“图”“强”的4个小球,除汉字不同外,小球没有任何区别,摸球前先搅拌均匀再摸球.如果摸一次同时取出2个球上的汉字恰能组成“奋发”或“图强”则小涵赢,否则小悦赢.(1)、用列表或树状图列出摸字的所有可能出现的情况.(2)、请判断该“摸字组词”游戏对小涵和小悦双方是否公平?并说明理由.21. 如图所示,一次函数y=kx+b与反比例函数y= 的图象交于A(2,4),B(﹣4,n)两点.
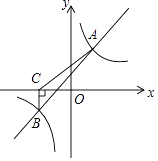 (1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.22. 如图,在矩形 中, , ,垂足分别为 、 ,连接 、 .
(1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.22. 如图,在矩形 中, , ,垂足分别为 、 ,连接 、 . (1)、求证: ;(2)、判断四边形 的形状,并说明理由.23. 随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
(1)、求证: ;(2)、判断四边形 的形状,并说明理由.23. 随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图. (1)、求本次调查的学生总人数,并补全条形统计图;(2)、求扇形统计图中“在线阅读”对应的扇形圆心角的度数;(3)、该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生人数.24. 专卖店卖某品牌文化衫,如果每件利润为30元(市场管理部门规定,该品牌文化衫每件利润不能超过50元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.(1)、请写出y与x之间的函数表达式;(写出自变量x的范围)(2)、当x为多少时,超市每天销售这种品牌文化衫可获利润1932元?(3)、设超市每天销售这种文化衫可获利w元,当x为多少时w最大,最大值是多少?25. 如图,以 为直径作半圆O,C是半圆上一点, 的平分线交 于点E,D为 延长线上一点,且 .
(1)、求本次调查的学生总人数,并补全条形统计图;(2)、求扇形统计图中“在线阅读”对应的扇形圆心角的度数;(3)、该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生人数.24. 专卖店卖某品牌文化衫,如果每件利润为30元(市场管理部门规定,该品牌文化衫每件利润不能超过50元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.(1)、请写出y与x之间的函数表达式;(写出自变量x的范围)(2)、当x为多少时,超市每天销售这种品牌文化衫可获利润1932元?(3)、设超市每天销售这种文化衫可获利w元,当x为多少时w最大,最大值是多少?25. 如图,以 为直径作半圆O,C是半圆上一点, 的平分线交 于点E,D为 延长线上一点,且 . (1)、求证: 为 的切线;(2)、若 ,求 的长.26. 如图, 是以 为底边的等腰三角形,A,C分别是一次函数 的图象与y轴,x轴的交点,点B在二次函数 的图象上,且该二次函数图象上存在一点D使四边形 能构成平行四边形.
(1)、求证: 为 的切线;(2)、若 ,求 的长.26. 如图, 是以 为底边的等腰三角形,A,C分别是一次函数 的图象与y轴,x轴的交点,点B在二次函数 的图象上,且该二次函数图象上存在一点D使四边形 能构成平行四边形. (1)、求该二次函数的表达式;(2)、动点P在线段 上从点A至点D运动,同时动点Q在线段 上从点C到点A运动,两点都是以每秒1个单位长度的速度运动,当其中一个点到达终点时,另一个点也随之停止.
(1)、求该二次函数的表达式;(2)、动点P在线段 上从点A至点D运动,同时动点Q在线段 上从点C到点A运动,两点都是以每秒1个单位长度的速度运动,当其中一个点到达终点时,另一个点也随之停止.①当 是直角三角形时,求P的坐标;
②四边形 的面积是否有最小值?若有,求出面积的最小值和点P的坐标;若没有,请说明理由.
27. 问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2. (1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;(3)、延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
(1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;(3)、延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.