江苏省徐州市县区2021年数学中考一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. -5的倒数是（）

A、5 B、-5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2011年徐州市接待国内外旅游人数约为24 800 000人次，该数据用科学记数法表示为（）

A、 $2 ． 48 \times 10^{7}$ B、 $2 ． 48 \times 10^{6}$ C、 $0 ． 248 \times 10^{8}$ D、 $248 \times 10^{5}$

查看试题解析
4. 下列运算中，正确的是（）

A、 $x^{3} + x^{3} = x^{6}$ B、 $x^{3} \cdot x^{9} = x^{27}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 $x \div x^{2} = x^{- 1}$

查看试题解析
5. 如图，点A，B，C在⊙O上，∠AOB=72°，则∠ACB等于（）

A、36° B、54° C、18° D、28°

查看试题解析
6.
某市6月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别是（　　）

A、21，21 B、21，21.5 C、21，22 D、22，22

查看试题解析
7. 如图，E是直线 $C A$ 上一点， $∠ F E A = 40 °$ ，射线 $E B$ 平分 $∠ C E F$ ， $G E ⊥ E F$ .则 $∠ G E B =$ （）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
8. 如图，菱形ABCD的两个顶点B，D在反比例函数y= $\frac{k}{x}$ 的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（1，1），∠ABC=60°，则k的值是（）

A、﹣5 B、﹣4 C、﹣3 D、﹣2

查看试题解析

二、填空题

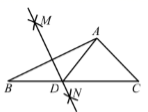
9. 4是　的算术平方根．

查看试题解析
10. 一个不透明的盒子中装有3个红球，2个黄球和1个绿球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是黄球的概率为．

查看试题解析
11. 使 $\sqrt{x - 6}$ 有意义的x的取值范围是．

查看试题解析
12. 若正多边形的一个内角等于140°，则这个正多边形的边数是．

查看试题解析
13. 已知关于x的一元二次方程x²﹣2x﹣a＝0有两个相等的实数根，则a的值是.

查看试题解析
14. 如图，在 $△ A B C$ 中， $B C = 9 ， A C = 4$ ，分别以点 $A 、 B$ 为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点 $M 、 N ，$ 作直线 $M N$ ，交 $B C$ 边于点 $D$ ，连接 $A D$ ，则 $△ A C D$ 的周长为.

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC.若∠CAB=22.5°，CD=8cm，则⊙O的半径为 cm.

查看试题解析
16. 如图，直线 $y = \frac{5}{2} x + 4$ 与x轴、y轴分别交于A、B两点，把 $△ A O B$ 绕点B逆时针旋转90°后得到 $△ A_{1} O_{1} B$ ，则点 $A_{1}$ 的坐标是.

查看试题解析
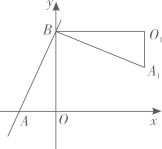17. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第n个图形中白色正方形的个数为.

查看试题解析
18. 如图，抛物线y＝ax²＋bx＋c（a≠0）与x轴交于点A、B，顶点为C，对称轴为直线x＝1，给出下列结论：①abc＜0；②若点C的坐标为（1，4），则△ABC的面积可以等于4；③M（x₁ ， y₁），N（x₂ ， y₂）是抛物线上两点（x₁＜x₂），若x₁＋x₂＞2，则y₁＜y₂；④若抛物线经过点（3，﹣1），则方程ax²＋bx＋c＋1＝0的两根为﹣1，3，其中正确结论的序号为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 1)}^{2020} - {(\frac{1}{3})}^{- 1} + \sqrt[3]{8}$ ；

(2)、 $\frac{x^{2} - 1}{x + 1} \div \frac{x^{2} - 2 x + 1}{x^{2} - x}$ .

查看试题解析
20.

(1)、解方程：x²﹣2x﹣3＝0；

(2)、解不等式组： ${\begin{array}{l} 2 x > 1 - x \\ 2 (2 x + 1) < x + 4 \end{array}$ .

查看试题解析
21. 为了丰富同学们的课余生活，冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动，围绕在绘画、剪纸、舞蹈、书法四类活动小组中，你最喜欢的哪一类？的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢绘画小组的学生人数占所调查人数的 $30 %$ ，请你根据图中提供的信息回答下列问题：

(1)、在这次调查中，一共抽取了多少名学生；

(2)、请通过计算补全条形统计图；

(3)、若冬威中学共有800名学生，请你估计该中学最喜欢剪纸小组的学生有多少名．

查看试题解析
22. 全面两孩政策实施后，甲、乙两个家庭有了各自的规划，假定生男生女的概率相同，回答下列问题：

(1)、甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是女孩的概率是；

(2)、乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率．

查看试题解析
23. 如图，在平行四边形ABCD中，点O是边BC的中点，连接DO并延长，交AB的延长线于点E，连接BD，EC.

(1)、求证：△BOE≌△COD；

(2)、当∠BOD＝°时，四边形BECD是菱形.

查看试题解析
24. 徐州至上海的铁路里程为650km．从徐州乘“C”字头列车A，“D”字头列车B都可到达上海，已知A车的平均速度为B车的2倍，且行驶时间比B车少2.5h．

(1)、设A车的平均速度是xkm/h，根据题意，可列分式方程：；

(2)、求A车的平均速度及行驶时间．

查看试题解析
25. 如图，梯子斜靠在与地面垂直（垂足为O）的墙上.当梯子位于AB位置时，它与地面所成的角∠ABO＝60°，当梯子底端向右滑动0.5m（即BD＝0.5m）到达CD位置时，它与地面所成的角∠CDO＝51°18′，求梯子的长.（参考数据：sin51°18′＝0.780，cos51°18′＝0.625，tan51°18′＝1.248）

查看试题解析
26. 小王骑车从甲地到乙地，小李骑车从乙地到甲地，小王的速度小于小李的速度，两人同时出发，沿同一条公路匀速前进.图中的折线表示两人之间的距离y（km）与小王的行驶时间x（h）之间的函数关系.请你根据图象进行探究：

(1)、小王的速度是km/h，小李的速度是km/h；

(2)、求线段BC所表示的y与x之间的函数表达式，并写出自变量x的取值范围.

(3)、求当两人相距18千米时，小王行驶多少小时？

查看试题解析
27. 如图1，一副直角三角板满足AB＝BC，AC＝DE，∠ABC＝∠DEF＝90°，∠EDF＝30°.将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q.

(1)、如图2，当 $\frac{C E}{E A}$ ＝1时， $\frac{E P}{E Q}$ ＝；

(2)、如图3，当 $\frac{C E}{E A}$ ＝2时，
①EP与EQ满足怎样的数量关系？并说明理由；

②在旋转过程中，连接PQ，若AC＝30cm，设EQ的长为xcm，△EPQ的面积为S（cm²）.求S关于x的函数表达式，并求出x的取值范围.

查看试题解析
28. 如图，已知二次函数y＝ax²＋bx＋3的图象与x轴交于点A（﹣1，0）、B（4，0），与y轴交于点C.

(1)、二次函数的表达式为；

(2)、点M在直线BC上，当△ABM为等腰三角形时，求点M的坐标；

(3)、若点E在二次函数的图象上，以E为圆心的圆与直线BC相切于点F，且EF＝ $\frac{6}{5}$ ，请直接写出点E的坐标.

查看试题解析