江苏省宿迁市泗洪县2021年数学中考二模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

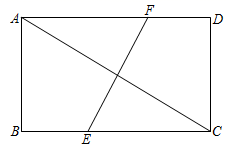
1. ﹣5的相反数是（）

A、﹣5 B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列计算中，正确的是（）

A、 $3 a + 2 a^{2} = 5 a^{3}$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(- 3 x^{3})}^{2} = 9 x^{6}$

查看试题解析
3. 肥皂泡的泡壁厚度大约是0.0007mm，0.0007用科学记数法表示为（　　）

A、0.7×10^﹣³ B、7×10^﹣³ C、7×10^﹣⁴ D、7×10^﹣⁵

查看试题解析
4. 如图，直线 $a / / b$ ，在 $R t Δ A B C$ 中，点 $C$ 在直线 $a$ 上，若 $∠ 1 = 58^{\circ} ， ∠ 2 = 24^{\circ}$ ，则 $∠ A$ 的度数为（）

A、56° B、34° C、36° D、24°

查看试题解析
5. 若一次函数 $y = - x + m$ 的图象经过点 $(- 1, 2)$ ，则不等式 $- x + m \geq 2$ 的解集为（）

A、 $x \geq 0$ B、 $x \leq 0$ C、 $x \geq - 1$ D、 $x \leq - 1$

查看试题解析
6. 如图， $A D$ 为 $Δ A B C$ 的外接圆 $⊙ O$ 的直径，若 $∠ B A D = 58^{\circ}$ ，则 $∠ A C B$ 等于（）

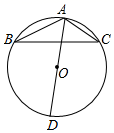A、32° B、36° C、48° D、52°

查看试题解析
7. 已知点 $M (m, 2021), N (n, 2021)$ 是二次函数 $y = a x^{2} + b x + 2020$ 图象上的两个不同的点，则当 $x = m + n$ 时，其函数值等于（）

A、2022 B、2021 C、2020 D、2019

查看试题解析
8. 如图，在 $Δ A B C$ 中， $A B = A C = 5 ， B C = 4 \sqrt{5}$ ， $D$ 为边 $A C$ 上一动点（ $C$ 点除外），把线段 $B D$ 绕着点 $D$ 沿着顺时针的方向旋转90°至 $D E$ ，连接 $C E$ ，则 $Δ C D E$ 面积的最大值为（）

A、16 B、8 C、32 D、10

查看试题解析

二、解答题

9. 不等式组 ${\begin{matrix} - x \leq 1 \\ x - 1 < 2 \end{matrix}$ 的解集是.

查看试题解析
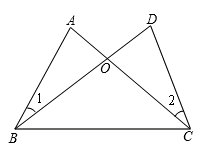
10. 计算： $2 \cos 45^{\circ} + {(π - 2021)}^{0} - | \sqrt{2} - 2 |$ .

查看试题解析
11. 先化简，再求值： $(1 - \frac{1}{a}) \div (\frac{a^{2} + 1}{a} - 2)$ ，其中 $a = \sqrt{2} + 1$ .

查看试题解析
12. 如图，已知AB=DC，AC=DB．求证：∠1=∠2．

查看试题解析
13. 有四张正面分别标有数字﹣2，0，2，3的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上洗均匀.

(1)、随机抽出一张卡片，则抽到数字绝对值为2的卡片概率为；

(2)、随机抽出一张卡片，记下数字后放回并搅匀，再随机抽出一张卡片，请用列表或画树状图的方法，求两次抽出的卡片上的数字之和是0的概率.

查看试题解析
14. 如图，某学校数学兴趣社团成员想测量斜坡 $C D$ 旁一棵树 $A B$ 的高度，他们先在点 $C$ 处测得树顶 $B$ 的仰角为60°，然后在坡顶 $D$ 测得树顶 $B$ 的仰角为30°，已知斜坡 $C D$ 的长度为 $8 m$ ， $D E$ 的长为 $4 m$ ，则树 $A B$ 的高度是多少米.

查看试题解析
15. 如图，以 $B D$ 为直径的 $⊙ O$ 经过点 $A$ .连接 $A B 、 A D (A B > A D)$ .

(1)、尺规作图：在 $B D$ 的延长线上作出点 $C$ ，使 $∠ C A D = ∠ A B D$ ；（要求保留作图痕迹，不写作法）

(2)、请判断直线 $A C$ 与 $⊙ O$ 的位置关系，并说明理由.

查看试题解析
16. 如图，已知反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点 $A (4 ， 2)$ ，过 $A$ 作 $A C ⊥ y$ 轴于点 $C$ .点 $B$ 为反比例函数图象上的一动点，过点 $B$ 作 $B D ⊥ x$ 轴于点 $D$ ，连接 $A D$ .直线 $B C$ 与 $x$ 轴的负半轴交于点 $E$ .

(1)、求 $k$ 的值；

(2)、若 $B D = 3 O C$ ，求四边形 $A C E D$ 的面积.

查看试题解析
17. 阳光小区计划对面积为 $1200 m^{2}$ 的区域进行停车位改造，经投标由甲、乙两个工程队来完成.已知甲队每天能完成改造的面积是乙队每天能完成改造面积的2倍，如果两队各自独立完成面积为 $400 m^{2}$ 区域的改造时，甲队比乙队少用4天.

(1)、求甲、乙两工程队每天各能完成多少面积的改造；

(2)、若甲队每天改造费用是1.2万元，乙队每天改造费用为0.5万元，社区要使这次改造的总费用不超过13万元，则至少应安排乙工程队改造多少天？

查看试题解析
18. 如图，在平面直角坐标系中，点 $A$ 坐标为 $(- 4 ， 0)$ ，点 $B$ 坐标为 $(4 ， 0)$ ，点 $C$ 为线段 $A B$ 上的一个动点，分别以 $A C 、 B C$ 为边在 $x$ 轴上方作正方形 $A C D E$ 和正方形 $B C G F$ ，连接 $E F$ 交直线 $C G$ 于点 $P$ ，设 $P$ 点坐标为 $(x ， y)$ .

(1)、当 $C$ 运动到点 $(- 2 ， 0)$ 时，求 $P$ 点坐标；

(2)、当点 $C$ 从点 $A$ 运动到点 $B$ 的过程中（包含 $A 、 B$ 两点），试求出点 $P$ 运动路径图象的函数表达式，并写出自变量的取值范围；

(3)、连接 $C E 、 C F$ ，在点 $C$ 的运动过程中，是否存在 $Δ P D E$ 和 $Δ C E F$ 相似，若存在，试求出 $P$ 点坐标，若不存在，请说明理由.

查看试题解析
19. （阅读）婆罗摩笈多是七世纪印度数学家，他曾提出一个定理：若圆内接四边形的对角线相互垂直，则垂直于一边且过对角线交点的直线平分对边.

证明：如图1所示内接于圆的四边形 $A B C D$ 的对角线 $A C ， B D$ 互相垂直，垂足为点 $G$ ，过点 $G$ 的直线垂直于 $A D$ ，垂足为点 $E$ ，与边 $B C$ 交于点 $F$ ，由垂直关系得 $∠ E G D + ∠ F G C = 90^{\circ}$ ， $∠ E G D + ∠ E D G = 90^{\circ}$ ，所以 $∠ E D G = ∠ F G C$ ，由同弧所对的圆周角相等得 $∠ A D B = ∠ A C B$ ，所以 $∠ F G C = ∠ F C G$ ，则 $F G = F C$ ，同理， $F G = F B$ ，故 $B F = F C$ ；

(1)、【思考】命题“若圆内接四边形的对角线相互垂直，则平分对边且过对角线交点的直线垂直于另一边”为（填“真命题”，“假命题”）；

(2)、【探究】如图2， $Δ A G B$ 和 $Δ D G C$ 为共顶点的等腰直角三角形， $∠ A G B = ∠ D G C = 90^{\circ}$ ，过点 $G$ 的直线垂直于 $A D$ ，垂足为点 $E$ ，与边 $B C$ 交于点 $F$ .证明：点 $F$ 是 $B C$ 的中点；

(3)、如图3， $Δ A G B$ 和 $Δ D G C$ 为共顶点的等腰直角三角形 $∠ A G B = ∠ D G C = 90^{\circ}$ ，点 $F$ 是 $B C$ 的中点，连接 $F G$ 交 $A D$ 于点 $E$ ，若 $G F = 2$ ，求 $A D$ 的长.

查看试题解析

三、填空题

20. 在函数y= $\frac{x}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
21. 将抛物线 $y = x^{2}$ 的图象向上平移3个单位，则平移后抛物线的函数表达式为.

查看试题解析
22. 在一次投篮比赛中，某小组8名同学的成绩（单位：分）分别是：6，10，7，7，8，6，9，6，则这组数据的中位数是.

查看试题解析
23. 用半径为6，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
24. 已知数轴上两点 $A 、 B$ 到原点的距离是 $\sqrt{2}$ 和2，则 $A B =$ .

查看试题解析
25. 已知 $a + b = 2$ ，则 $a^{2} - b^{2} + 4 b =$ ．

查看试题解析
26. 如图，曲线C₂是双曲线C₁：y= $\frac{6}{x}$ （x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C₂上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于.

查看试题解析
27. 如图，矩形 $A B C D$ 中，对角线 $A C$ 的垂直平分线 $E F$ 分别交 $B C$ ， $A D$ 于点 $E ， F$ ，若 $B E = 4 ， A F = 6$ ，则 $A C$ 的长为.

查看试题解析
28. 面积为2的 $▱ A B C D$ 的边 $A B$ 和 $C D$ 被分为3等份，边 $A D$ 和 $B C$ 被分为4等份，按如图所示的方式连接分点，则图中形成的小平行四边形的面积 $S =$ .

查看试题解析