江苏省无锡市宜兴市和桥联盟2021年数学中考模拟试卷(3月)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、 B、 C、 D、22. 函数 中自变量 的取值范围是( )A、 B、 C、 D、3. sin60°=( )A、 B、 C、1 D、4. 下列图标中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,左图是由4个大小相同的正方体组合而成的几何体,其主视图是( )
5. 如图,左图是由4个大小相同的正方体组合而成的几何体,其主视图是( )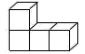 A、
A、 B、
B、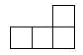 C、
C、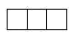 D、
D、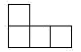 6. 已知某圆锥的底面半径为3cm,母线长5cm,则它的侧面展开图的面积为( )A、30cm2 B、15cm2 C、30πcm2 D、15πcm27. 新冠疑似病例需在定点医院隔离观察,要掌握他在一周内的体温是否稳定,则医生需要了解这位病人7天体温的( )A、中位数 B、平均数 C、方差 D、众数8. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直平分的四边形是菱形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形9. 如图,曲线 是抛物线 的一部分(其中 是抛物线与 轴的交点, 是顶点),曲线 是双曲线 的一部分.曲线 与 组成图形 .由点 开始不断重复图形 形成一组“波浪线”.若点 , 在该“波浪线”上,则 的最大值为( )
6. 已知某圆锥的底面半径为3cm,母线长5cm,则它的侧面展开图的面积为( )A、30cm2 B、15cm2 C、30πcm2 D、15πcm27. 新冠疑似病例需在定点医院隔离观察,要掌握他在一周内的体温是否稳定,则医生需要了解这位病人7天体温的( )A、中位数 B、平均数 C、方差 D、众数8. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直平分的四边形是菱形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形9. 如图,曲线 是抛物线 的一部分(其中 是抛物线与 轴的交点, 是顶点),曲线 是双曲线 的一部分.曲线 与 组成图形 .由点 开始不断重复图形 形成一组“波浪线”.若点 , 在该“波浪线”上,则 的最大值为( )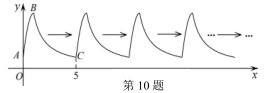 A、5 B、6 C、2020 D、202110. 如图,矩形 中, 是 上一点,连接 ,将矩形沿 翻折,使点 落在 边 处,连接 ,在 上取点 ,以 为圆心, 长为半径作⊙O与 相切于点 .若 , ,则下列结论:① 是 的中点;②⊙O的半径是2;③ ;④S阴影 .其中正确的结论有( )
A、5 B、6 C、2020 D、202110. 如图,矩形 中, 是 上一点,连接 ,将矩形沿 翻折,使点 落在 边 处,连接 ,在 上取点 ,以 为圆心, 长为半径作⊙O与 相切于点 .若 , ,则下列结论:① 是 的中点;②⊙O的半径是2;③ ;④S阴影 .其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
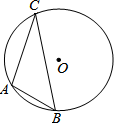
11. 因式分解:3x2﹣12= .12. 电影《流浪地球》中,人类计划带着地球一起逃到距地球4光年的半人马星座比邻星.已知光年是天文学中的距离单位,4光年大约是381000亿千米,该数据用科学记数法表示为亿千米.13. 已知正多边形的一个外角为72°,则该正多边形的内角和为.14. 写出一个 关于 的函数关系式:满足在第一象限内, 随 的增大而增大的函数是.15. 如图,已知 的直径为 , 、 、 三点在 上,且 ,则 长.
 16. 如图,菱形 的边 轴,垂足为点 ,顶点 在第二象限,顶点 在 轴的正半轴上,反比例函数 的图象同时经过顶点 、 ,若点 的横坐标为1, .则 的值为.
16. 如图,菱形 的边 轴,垂足为点 ,顶点 在第二象限,顶点 在 轴的正半轴上,反比例函数 的图象同时经过顶点 、 ,若点 的横坐标为1, .则 的值为. 17. 如图,扇形 中, ,将扇形 绕点 逆时针旋转,得到扇形 ,若点 刚好落在弧 上的点 处,则 的值为.
17. 如图,扇形 中, ,将扇形 绕点 逆时针旋转,得到扇形 ,若点 刚好落在弧 上的点 处,则 的值为.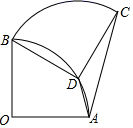
三、解答题
-
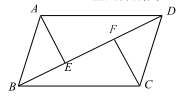
18. 计算:(1)、 ;(2)、 .19.(1)、解方程: ;(2)、解不等式组 .20. 如图, 为 的对角线, , ,垂足分别为 、 .求证: .
 21. 太仓人杰地灵,为了了解学生对家乡历史文化名人的知晓情况,某校对部分学生进行了随机抽样调查,并将调查结果绘制成如图所示统计图的一部分.
21. 太仓人杰地灵,为了了解学生对家乡历史文化名人的知晓情况,某校对部分学生进行了随机抽样调查,并将调查结果绘制成如图所示统计图的一部分.
根据统计图中的信息,回答下列问题:
(1)、本次抽样调查的样本容量是;(2)、在扇形统计图中,“了解很少”所在扇形的圆心角是度;(3)、若全校共有学生1300人,那么该校约有多少名学生“基本了解”太仓的历史文化名人?22. 2020春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,江阴初级中学开通了三条人工测体温的通道,每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师),周一有小卫和小孙两学生进校园,在3个人工测体温通道中,可随机选择其中的一个通过.(1)、求小孙进校园时,由王老师测体温的概率;(2)、求两学生进校园时,都是王老师测体温的概率.23. 已知:如图,在△ABC中,AB=AC,AE是∠BAC的平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径. (1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= 时,求⊙O的半径.24. 城市内环高架能改善整个城市的交通状况.在一般情况下,高架上的车流速度 (单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当高架上的车流密度达到188辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过28辆/千米时,车流速度为80千米/小时.研究表明:当 时,车流速度 是车流密度 的一次函数.(1)、当 时,求车流速度 关于车流密度 的函数解析式;(2)、若车流速度 不低于50千米/小时,求车流密度 为多大时,车流量 (单位时间内通过高架桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.25. 如图,在边长为1小正方形的网格中,△ABC的顶点A、B、C均落在格点上,请用无刻度的直尺按要求作图.(保留画图痕迹,不需证明)
(1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= 时,求⊙O的半径.24. 城市内环高架能改善整个城市的交通状况.在一般情况下,高架上的车流速度 (单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当高架上的车流密度达到188辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过28辆/千米时,车流速度为80千米/小时.研究表明:当 时,车流速度 是车流密度 的一次函数.(1)、当 时,求车流速度 关于车流密度 的函数解析式;(2)、若车流速度 不低于50千米/小时,求车流密度 为多大时,车流量 (单位时间内通过高架桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.25. 如图,在边长为1小正方形的网格中,△ABC的顶点A、B、C均落在格点上,请用无刻度的直尺按要求作图.(保留画图痕迹,不需证明) (1)、如图①,点P在格点上,在线段AB上找出所有符合条件的点Q,使△APQ和△ABC相似;(2)、如图②,在AC上作一点M,使以M为圆心,MC为半径的⊙M与AB相切,并直接写出此时⊙M的半径为 ▲ .26. 如图,二次函数 的图象与 轴交于 、 两点(点 在点 的右边),与 轴交于点 .
(1)、如图①,点P在格点上,在线段AB上找出所有符合条件的点Q,使△APQ和△ABC相似;(2)、如图②,在AC上作一点M,使以M为圆心,MC为半径的⊙M与AB相切,并直接写出此时⊙M的半径为 ▲ .26. 如图,二次函数 的图象与 轴交于 、 两点(点 在点 的右边),与 轴交于点 .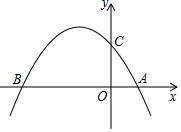 (1)、请直接写出 、 两点的坐标: , ;(2)、若以 为直径的圆恰好经过这个二次函数图象的顶点.
(1)、请直接写出 、 两点的坐标: , ;(2)、若以 为直径的圆恰好经过这个二次函数图象的顶点.①求这个二次函数的表达式;
②若 为二次函数图象位于第二象限部分上的一点,过点 作 平行于 轴,交直线 于点 .连接 、 ,是否存在一个点 ,使 ?如果存在,请求出点 的坐标;如果不存在,请说明理由.
27. 将一矩形纸片 放在直角坐标系中, 为原点, 在 轴上, , . (1)、如图1,在 上取一点 ,将 沿 折叠,使 点落至 边上的 点,求直线 的解析式;(2)、如图2,在 、 边上选取适当的点 、 ,将 沿 折叠,使 点落在 边上的 点,过 作 于点 点,交 于 点.
(1)、如图1,在 上取一点 ,将 沿 折叠,使 点落至 边上的 点,求直线 的解析式;(2)、如图2,在 、 边上选取适当的点 、 ,将 沿 折叠,使 点落在 边上的 点,过 作 于点 点,交 于 点.①求证: ;
②设 ,探求 与 满足的等量关系式,并将 用含 的代数式表示(指出变量 的取值范围);
(3)、在(2)的条件下,当 时,点 在直线 上,问坐标轴上是否存在点 ,使以 、 、 、 为顶点的四边形是平行四边形,若存在,请直接写出 点坐标;若不存在,请说明理由.