江苏省无锡市新吴区新一教育集团2021年数学中考模拟试卷(4月)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. ﹣5的相反数是( )A、5 B、±5 C、﹣5 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列几何体中,俯视图是矩形的是( )A、
 B、
B、 C、
C、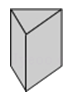 D、
D、 4.
4.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
 A、75° B、55° C、40° D、35°5. 我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4=4.5 D、1.4(1+x)+1.4=4.56. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( )
A、75° B、55° C、40° D、35°5. 我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4=4.5 D、1.4(1+x)+1.4=4.56. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( ) A、20° B、25° C、40° D、50°7. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A、20° B、25° C、40° D、50°7. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )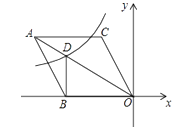 A、 B、- C、 D、-8. 如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( )
A、 B、- C、 D、-8. 如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 小明同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜索到与之相关结果的条数是1650000,这个数用科学记数法表示为.10. 函数 中自变量x的取值范围是 .11. 分解因式: = .12. 已知圆锥的底面半径是3cm,母线长是5cm,则圆锥的侧面积为cm2 . (结果保留π)13. 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为
 14. 如图,点 是正方形 内一点,点 到点 , 和 的距离分别为1, , ,延长 与 相交于点 ,则 的长为.
14. 如图,点 是正方形 内一点,点 到点 , 和 的距离分别为1, , ,延长 与 相交于点 ,则 的长为.
三、解答题
-
15. 计算:(1)、 ;(2)、 .16.(1)、解不等式 ,并把它的解集在数轴上表示出来;(2)、解方程组 .17. 现有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字 , ,0,现从甲袋中随机抽取一个小球,记录标有的数字为 ,再从乙袋中随机抽取一个小球,记录标有的数字为 ,确定点 坐标为 ,求点 在函数 的图象上的概率.(用树状图法或列表法表示)18. 某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
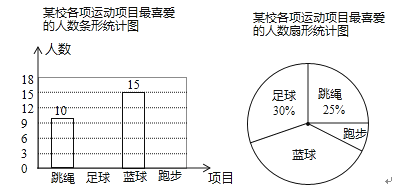 (1)、求本次被调查的学生人数;
(1)、求本次被调查的学生人数;
(2)、补全条形统计图;
(3)、该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?19. 如图,平行四边形 中, . (1)、利用尺规作图,在 边上确定点 ,使点 到边 , 的距离相等(不写作法,保留作图痕迹);(2)、若 , ,求 的长.20. 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)、利用尺规作图,在 边上确定点 ,使点 到边 , 的距离相等(不写作法,保留作图痕迹);(2)、若 , ,求 的长.20. 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.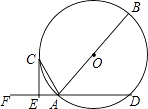 (1)、求证:CE是⊙O的切线;(2)、若AE=1,CE=2,求⊙O的半径.21. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
(1)、求证:CE是⊙O的切线;(2)、若AE=1,CE=2,求⊙O的半径.21. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1 , W2(单位:元)
(1)、用含x的代数式分别表示W1 , W2;
(2)、当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?22. 已知 , 分别为四边形 和 的对角线,点 在 内, . (1)、当四边形ABCD和EFCG均为正方形时,求证: ∽ ;(2)、如图①,当四边形 和 均为正方形时,连接 ,若 , ,求 的长.(3)、如图②,当四边形 和 均为矩形,且 时,若 , , ,求 的值.23. 如图,在平面直角坐标系 中,抛物线 ( )与 轴交于 、 两点(点 在点 的左侧),与 轴交于 点,经过点 的直线 : 与 轴负半轴交于点 ,与抛物线的另一个交点为 ,且 .
(1)、当四边形ABCD和EFCG均为正方形时,求证: ∽ ;(2)、如图①,当四边形 和 均为正方形时,连接 ,若 , ,求 的长.(3)、如图②,当四边形 和 均为矩形,且 时,若 , , ,求 的值.23. 如图,在平面直角坐标系 中,抛物线 ( )与 轴交于 、 两点(点 在点 的左侧),与 轴交于 点,经过点 的直线 : 与 轴负半轴交于点 ,与抛物线的另一个交点为 ,且 . (1)、直接写出点 的坐标,并求直线 的函数表达式(其中 、 用含 的式子表示);(2)、是否存在 和相应的 轴正半轴上一点 ,使得 与 相似,如果存在,求出所有 的值和点 的坐标;若不存在,请说明理由.
(1)、直接写出点 的坐标,并求直线 的函数表达式(其中 、 用含 的式子表示);(2)、是否存在 和相应的 轴正半轴上一点 ,使得 与 相似,如果存在,求出所有 的值和点 的坐标;若不存在,请说明理由.