江苏省南通市通州区2021年中考数学模拟试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、-3 B、3 C、 D、2. 计算 的结果是( )A、 B、a C、 D、3. 下列水平放置的几何体中,俯视图是矩形的是( )A、圆柱
 B、长方体
B、长方体 C、三棱柱
C、三棱柱  D、圆锥
D、圆锥 4. 有一组数据:2,5,5,6,7,这组数据的平均数为( )A、6 B、5 C、4 D、35. 不等式组 的解集在数轴上表示正确的是( )A、
4. 有一组数据:2,5,5,6,7,这组数据的平均数为( )A、6 B、5 C、4 D、35. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、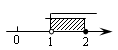 D、
D、 6. 一元二次方程 配方后化为( )A、 B、 C、 D、7. 如图,函数y=kx+b(k≠0)与y= (m≠0)的图象交于点A(2,3),B(-6,-1),则不等式kx+b> 的解集为( )
6. 一元二次方程 配方后化为( )A、 B、 C、 D、7. 如图,函数y=kx+b(k≠0)与y= (m≠0)的图象交于点A(2,3),B(-6,-1),则不等式kx+b> 的解集为( )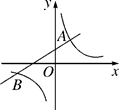 A、x<-6或0<x<2 B、-6<x或x>2 C、 D、8. 某商店今年1月份的销售额是1万元,3月份的销售额是1.21万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、15% C、10% D、5%9. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、x<-6或0<x<2 B、-6<x或x>2 C、 D、8. 某商店今年1月份的销售额是1万元,3月份的销售额是1.21万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、15% C、10% D、5%9. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ) A、4 B、5 C、6 D、710. 如图,在正方形 外侧作直线 ,点C关于直线 的对称点为M,连接 , .其中 交直线 于点N.若 ,则当 时,正方形 的边长为( )
A、4 B、5 C、6 D、710. 如图,在正方形 外侧作直线 ,点C关于直线 的对称点为M,连接 , .其中 交直线 于点N.若 ,则当 时,正方形 的边长为( ) A、 B、5 C、 D、
A、 B、5 C、 D、二、填空题
-
11. 已知一个多边形的每一个外角都等于72°,则这个多边形的边数是.12. 已知方程组 的解为 ,则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为 .13. 计算( - )× 的结果是 .14. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=.
 15. 已知 ,则 . .16. 如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为 .
15. 已知 ,则 . .16. 如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为 . 17. 如图,点A在函数y= (x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为.
17. 如图,点A在函数y= (x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为. 18. 已知关于x的二次函数y=ax2+(a2-1)x-a的图象与
18. 已知关于x的二次函数y=ax2+(a2-1)x-a的图象与 轴的一个交点的坐标为(m,0),若2<m<3,则a的取值范围是.
轴的一个交点的坐标为(m,0),若2<m<3,则a的取值范围是. 三、解答题
-
19.
(1)、计算 (-2)2+( -π)0+|1— |;(2)、解方程组:20. 先化简,再求值: ,其中 .21. 某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
各部门人数及每人所创年利润统计表
部门
员工人数
每人所创的年利润/万元
A
5
10
B
b
8
C

5
(1)、①在扇形图中,C部门所对应的圆心角的度数为;②在统计表中,b= , c=;
(2)、求这个公司平均每人所创年利润.22. 现有一组数:-1, ,0,5,求下列事件的概率:(1)、从中随机选择一个数,恰好选中无理数;(2)、从中随机选择两个不同的数,均比0大.23. 如图,已知 的直径 ,弦 ,D是 的中点,过点D作 ,交 的延长线于点E.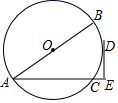 (1)、求证: 是 的切线;(2)、求 的长.24. 已知抛物线 .
(1)、求证: 是 的切线;(2)、求 的长.24. 已知抛物线 . (1)、求抛物线 的对称轴;(2)、过点 作y轴的垂线,与抛物线 交于不同的两点M,N(不妨设点M在点N的左侧).
(1)、求抛物线 的对称轴;(2)、过点 作y轴的垂线,与抛物线 交于不同的两点M,N(不妨设点M在点N的左侧).①当 时,求线段 的长;
②当 时,若 ,求a的值;
③当 时,若 ,直接写出a的取值范围.
25. 在 中, 于点 . (1)、如图1,当点 是线段 的中点时,
(1)、如图1,当点 是线段 的中点时,① 的长为;
②延长 至点 ,使得 ,此时 与 的数量关系是 , 与 的数量关系是;
(2)、如图2,当点 不是线段 的中点时,画 (点 与点 在直线 的异侧),使 ,连接 .①按要求补全图形;
②求 的长.
26.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
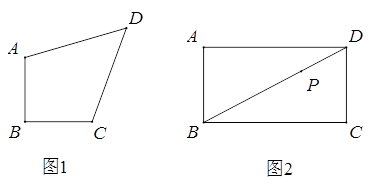 (1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
(1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)、如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.