江苏省常州市2021年数学中考新课结课试卷(4月)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 在平面直角坐标系中,点(2,6)关于原点对称的点的坐标是( )A、(﹣2,﹣6) B、(﹣2,6) C、(﹣6,﹣2) D、(6,2)2. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:
跳高成绩
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1
这些运动员跳高成绩的中位数和众数分别是( )
A、1.65,1.70 B、1.70,1.65 C、1.60,1.70 D、3,54. 如图,⊙O的弦AB=6,M是AB上任意一点,且OM最小值为4,⊙O的半径为( ) A、5 B、4 C、3 D、25. 已知半径为5的⊙O是△ABC的外接圆.若∠ABC=25°,则劣弧 的长为( )A、 B、 C、 D、6. 关于二次函数y=(x-1)2+2,下列说法正确的是( )A、图象与y轴的交点坐标为(0,2) B、图象的对称轴在y轴的左侧 C、y的最大值为2 D、当x>1时,y的值随x值的增大而增大7. 已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为2的点共有( )A、1个 B、2个 C、3个 D、4个8. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A、5 B、4 C、3 D、25. 已知半径为5的⊙O是△ABC的外接圆.若∠ABC=25°,则劣弧 的长为( )A、 B、 C、 D、6. 关于二次函数y=(x-1)2+2,下列说法正确的是( )A、图象与y轴的交点坐标为(0,2) B、图象的对称轴在y轴的左侧 C、y的最大值为2 D、当x>1时,y的值随x值的增大而增大7. 已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为2的点共有( )A、1个 B、2个 C、3个 D、4个8. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )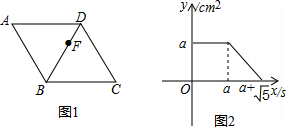 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题
-
9. 若 ,则锐角 的度数是.10. 已知一元二次方程 有一个根为 ,则另一根为.11. 如果一个正多边形的每一个外角都是 ,那么这个多边形是边形.12. 一个不透明的口袋中装有1个黄球和1白球,它们除颜色外都相同,搅匀后从中任意摸出1个球然后放回,再搅匀任意摸出1个球,小红第1次摸到的是黄球,那么小红第2次摸到黄球的概率是.13. 某农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种甜玉米各用10块试验田进行实验,得到这两个品种甜玉米每公顷产量的两组数据(如图所示).根据图6中的信息,可知在试验田中,种甜玉米的产量比较稳定.
 14. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为℃.15. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,DE=40cm,测得边DF离地面的高度AC=1.5m,CD=12m,则树高AB=.
14. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为℃.15. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,DE=40cm,测得边DF离地面的高度AC=1.5m,CD=12m,则树高AB=. 16. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC= .
16. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC= . 17. 如图,以点C(0,1)为位似中心,将△ABC按相似比1:2缩小,得到△DEC,则点A(1,﹣1)的对应点D的坐标为.
17. 如图,以点C(0,1)为位似中心,将△ABC按相似比1:2缩小,得到△DEC,则点A(1,﹣1)的对应点D的坐标为. 18. 如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF= ,则点F与点C的最小距离为.
18. 如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF= ,则点F与点C的最小距离为.
三、解答题
-
19. 计算: .20. 解下列方程:(1)、x2﹣6x﹣3=0;(2)、3x(x﹣1)=2(1﹣x).21. 我市某校想知道学生对家乡旅游品牌的了解程度,随机抽取了部分学生进行问卷调查,问卷有四个选项(每位被调查的学生必选且只选一项)A.十分了解,B.了解较多,C.了解较少,D.不知道.将调查的结果绘制成如下两幅不完整的统计图,根据两幅统计图中的信息回答下列问题
 (1)、本次调查了多少名学生?补全条形统计图;(2)、扇形统计图中,A选项所对应扇形的圆心角度数为多少?(3)、该校共有500名学生,请你估计“不知道”的学生有多少名?22. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、若随机抽取1名,则恰好抽中甲的概率是;(2)、若随机抽取2名,试用画树状图或列表的方法表示所有可能的结果,并求出甲在其中的概率.23. 将线段 放在正方形网格中,点A、点B均在格点上.请你分别按要求在下图中画点C(点C在格点上).
(1)、本次调查了多少名学生?补全条形统计图;(2)、扇形统计图中,A选项所对应扇形的圆心角度数为多少?(3)、该校共有500名学生,请你估计“不知道”的学生有多少名?22. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、若随机抽取1名,则恰好抽中甲的概率是;(2)、若随机抽取2名,试用画树状图或列表的方法表示所有可能的结果,并求出甲在其中的概率.23. 将线段 放在正方形网格中,点A、点B均在格点上.请你分别按要求在下图中画点C(点C在格点上). (1)、在图1中画 ,使得 的值为 ;(2)、在图2中画 ,使得 的值为1;(3)、在图3中画钝角 ,使得 的值为 (请画出2种不同的图形).24. 某购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD与地平线的夹角为18°,一楼到地下停车场地面的距离CD=2.8米,地平线到一楼的垂直距离BC=1米.
(1)、在图1中画 ,使得 的值为 ;(2)、在图2中画 ,使得 的值为1;(3)、在图3中画钝角 ,使得 的值为 (请画出2种不同的图形).24. 某购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD与地平线的夹角为18°,一楼到地下停车场地面的距离CD=2.8米,地平线到一楼的垂直距离BC=1米. (1)、应在地面上距点B多远的A处开始斜坡施工?(精确到0.1米)(2)、如果给该购物广场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)25. 某百货商店服装柜在销售中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件.(1)、若想要这种童装销售利润每天达到1200元,同时又能让顾客得到更多的实惠,每件童装应降价多少元?(2)、当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?26. 如图,P为x轴正半轴上一点,过点P作x轴的垂线,交函数 的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交 于点C,连结 .
(1)、应在地面上距点B多远的A处开始斜坡施工?(精确到0.1米)(2)、如果给该购物广场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)25. 某百货商店服装柜在销售中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件.(1)、若想要这种童装销售利润每天达到1200元,同时又能让顾客得到更多的实惠,每件童装应降价多少元?(2)、当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?26. 如图,P为x轴正半轴上一点,过点P作x轴的垂线,交函数 的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交 于点C,连结 . (1)、当点P的坐标为 时,求 的面积;(2)、当点P的坐标为 时, 的面积是否随t值的变化而变化?27.
(1)、当点P的坐标为 时,求 的面积;(2)、当点P的坐标为 时, 的面积是否随t值的变化而变化?27. (1)、(问题情境)
(1)、(问题情境)射影定理:如图1,在 中, ,如果 ,垂足为D,那么有① ;② ;③ ;请你证明射影定理中的结论③即 .
(2)、(结论运用:请直接使用射影定理解决下列问题)如图2,正方形 的边长为6,点O是对角线 的交点,点E在 上,过点C作 ,垂足为F,连接 ,
①求证: ;
②若 ,求 的长.
28. 如图,抛物线 与x轴交于 两点,与y轴交于点C,直线 与该抛物线交于 两点. (1)、求抛物线的表达式.(2)、P是直线 下方抛物线上的一个动点,作 于点H,求 的最大值.(3)、以点C为圆心,1为半径作圆, 上是否存在点D,使得 是以 为直角边的直角三角形?若存在直接写出点D的坐标;若不存在,则说明理由.
(1)、求抛物线的表达式.(2)、P是直线 下方抛物线上的一个动点,作 于点H,求 的最大值.(3)、以点C为圆心,1为半径作圆, 上是否存在点D,使得 是以 为直角边的直角三角形?若存在直接写出点D的坐标;若不存在,则说明理由.