湖南省娄底市新化县2021年数学中考模拟试卷(一)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. |-2021|的结果是( )A、2021 B、-2021 C、 D、2. 下列图形中既是轴对称图形,也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、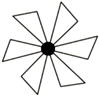 3. 下列运算正确的是( )A、 B、 C、 D、4. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、5. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差6. 不等式3(1﹣x)>2﹣4x的解在数轴上表示正确的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、5. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差6. 不等式3(1﹣x)>2﹣4x的解在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、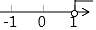 7. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )
7. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )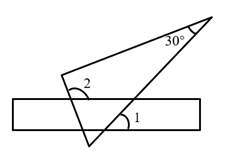 A、80° B、100° C、110° D、120°8. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、80° B、100° C、110° D、120°8. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )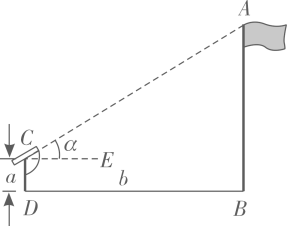 A、 B、 C、 D、9. 往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
A、 B、 C、 D、9. 往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )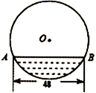 A、8cm B、10cm C、14cm D、16cm10. 如图,点 在双曲线 上,点 在双曲线 上,且 轴,点 、 在 轴上,若四边形 为矩形,则它的面积为( )
A、8cm B、10cm C、14cm D、16cm10. 如图,点 在双曲线 上,点 在双曲线 上,且 轴,点 、 在 轴上,若四边形 为矩形,则它的面积为( ) A、6 B、8 C、10 D、1211. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )
A、6 B、8 C、10 D、1211. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( ) A、148 B、152 C、168 D、17412. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4
A、148 B、152 C、168 D、17412. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4二、填空题
-
13. 使 有意义的 的取值范围是.14. 在平面直角坐标系中,点A(a,2)与点B(6,b)关于原点对称,则ab=.15. 已知 ,则代数式 的值是.16. 如图所示的电路图中,在开关全部断开的情况下,闭合其中任意一个开关,灯泡发亮的概率是 .
 17. 如图,在平行四边形 中, 平分 , ,连接 , 是 的中点,连接 ,若 ,则 .
17. 如图,在平行四边形 中, 平分 , ,连接 , 是 的中点,连接 ,若 ,则 .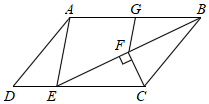 18. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
18. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
三、解答题
-
19. 计算∶20. 先化简,再求值:
,其中a,b是一元二次方程 的两个实数根.
21. 某校对九年级学生进行一次综合文科中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.等级
频数(人数)
频率
A
a
20%
B
16
40%
C
b
m
D
4
10%
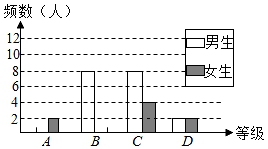
请你根据统计图表提供的信息解答下列问题:
(1)、上表中的a , b= , m=.(2)、本次调查共抽取了多少名学生?请补全条形图.(3)、若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )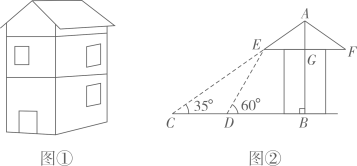 (1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).23. 某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进单批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.(1)、4月份进了这批T恤衫多少件?(2)、4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
(1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).23. 某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进单批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.(1)、4月份进了这批T恤衫多少件?(2)、4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.①用含a的代数式表示b;
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
24. 如图,在 中, ,以AB为直径的 分别交AC、BC于点D、E , 点F在AC的延长线上,且 .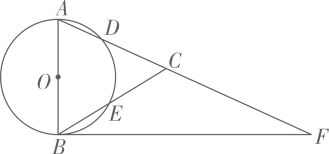 (1)、求证:BF是 的切线;(2)、若 的直径为4, ,求 .25. 如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)、求证:BF是 的切线;(2)、若 的直径为4, ,求 .25. 如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.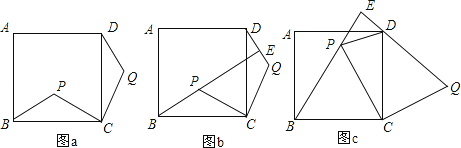 (1)、如图a,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E.
(1)、如图a,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E.①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
26. 如图,二次函数 的图象与 轴交于点 , ,与 轴交于点 ,抛物线的顶点为 ,其对称轴与线段 交于点 ,垂直于 轴的动直线 分别交抛物线和线段 于点 和点 ,动直线 在抛物线的对称轴的右侧(不含对称轴)沿 轴正方向移动到 点.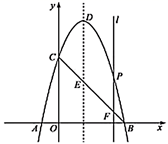 (1)、求出二次函数 和 所在直线的表达式;(2)、在动直线 移动的过程中,试求使四边形 为平行四边形的点 的坐标;(3)、连接 , ,在动直线 移动的过程中,抛物线上是否存在点 ,使得以点 , , 为顶点的三角形与 相似,如果存在,求出点 的坐标,如果不存在,请说明理由.
(1)、求出二次函数 和 所在直线的表达式;(2)、在动直线 移动的过程中,试求使四边形 为平行四边形的点 的坐标;(3)、连接 , ,在动直线 移动的过程中,抛物线上是否存在点 ,使得以点 , , 为顶点的三角形与 相似,如果存在,求出点 的坐标,如果不存在,请说明理由.