湖北省咸宁市四校2021年数学中考模拟联考试卷(3月)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 下列运算中,不正确的是( )A、 B、 C、 D、3. 下面几何体中,同一几何体的主视图和俯视图相同的是( )
 A、1个 B、2个 C、3个 D、4个4. 如图,已知 ,若 ,则 等于( )
A、1个 B、2个 C、3个 D、4个4. 如图,已知 ,若 ,则 等于( ) A、 B、 C、 D、5. “人间四月天,麻城看杜鹃”,2016年麻城市杜鹃花期间共接待游客约1200000人次,同比增长约26%,将1200000用科学记数法表示应是( )A、12×105 B、1.2×106 C、1.2×105 D、0.12×1056. 使代数式 有意义的x的取值范围是( )A、 B、 C、 D、 且7. 麻城市思源实验学校篮球队12名队员的年龄如下表:
A、 B、 C、 D、5. “人间四月天,麻城看杜鹃”,2016年麻城市杜鹃花期间共接待游客约1200000人次,同比增长约26%,将1200000用科学记数法表示应是( )A、12×105 B、1.2×106 C、1.2×105 D、0.12×1056. 使代数式 有意义的x的取值范围是( )A、 B、 C、 D、 且7. 麻城市思源实验学校篮球队12名队员的年龄如下表:年龄:(岁)
13
14
15
16
人数
2
5
4
1
关于这12名队员的年龄,下列说法错误的是( )
A、众数是14 B、极差是3 C、中位数是14 D、平均数是14.88. 如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )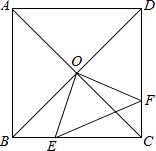 A、
A、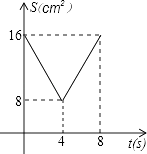 B、
B、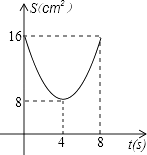 C、
C、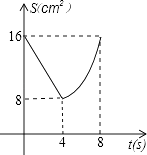 D、
D、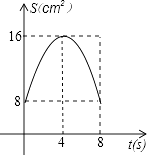
二、填空题
-
9. 分解因式:x2+2xy+y2﹣4=.10. 如果实数a,b满足a+b=6,ab=8,那么a2+b2=.11. 化简 的结果为12. 计算: .13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
 14. 如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.
14. 如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.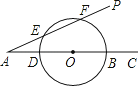 15. 在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC饶边AC所在的直线旋转一周得到圆锥,则该圆锥的表面积是.16. 如图,矩形 中, ,点E是 边上一点,连接 ,把 沿 折叠,使点B落在点F处,当 为直角三角形时, 的长为.
15. 在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC饶边AC所在的直线旋转一周得到圆锥,则该圆锥的表面积是.16. 如图,矩形 中, ,点E是 边上一点,连接 ,把 沿 折叠,使点B落在点F处,当 为直角三角形时, 的长为.
三、解答题
-
17. 解不等式组 ,并把它的解集在数轴上表示出来.18. 如图所示, 内一点 满足 于点 ,且 , .找出图中一条与 相等的线段,并加以证明.
 19. 端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?20. 每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).
19. 端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?20. 每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整). (1)、补全条形统计图和扇形统计图;(2)、若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?(3)、要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .21. 已知,如图, 是 的直径,点 为 上一点, 于点 ,交 于点 . 与 交于点 ,点 为 的延长线上一点,且 .
(1)、补全条形统计图和扇形统计图;(2)、若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?(3)、要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .21. 已知,如图, 是 的直径,点 为 上一点, 于点 ,交 于点 . 与 交于点 ,点 为 的延长线上一点,且 . (1)、求证: 是 的切线;(2)、求证: .22. 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为 海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.
(1)、求证: 是 的切线;(2)、求证: .22. 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为 海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截. (1)、求可疑船只的速度及点B到直线CD的距离;(2)、若军舰航行速度为20海里/时,可侦测半径为10海里,问军舰最快几小时可以侦测到可疑船只?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)23. 如图,已知正比例函数 和反比例函数 的图象交于A、B两点,若A点的纵坐标为 .
(1)、求可疑船只的速度及点B到直线CD的距离;(2)、若军舰航行速度为20海里/时,可侦测半径为10海里,问军舰最快几小时可以侦测到可疑船只?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)23. 如图,已知正比例函数 和反比例函数 的图象交于A、B两点,若A点的纵坐标为 . (1)、求反比例函数的解析式和点B坐标;(2)、根据图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)、若C是双曲线上的动点,D是x轴上的动点,是否存在这样的点C和点D,使以A、B、C、D为顶点的四边形是平行四边形?若存在,求出C、D坐标;若不存在,请说明理由.24. 某水产经销商从批发市场以30元每千克的价格收购了1000千克的虾,了解到市场价在30元每千克的基础上一个月内会以每天0.5元每千克的价格上涨,经销商打算先在塘里放养几天后再出售(但不超过一个月).假设放养期间虾的个体质量保持不变,但每天有10千克的虾死去.死去的虾会在当天以20元每千克的价格售出.(1)、若放养8天后出售,则活虾的市场价为每千克元.(2)、若放养x天后将活虾一次性售出,总共获得的销售总额y元,求y与x的函数关系式;(3)、若放养期间,每天会有各种其他的各种费用支出为a元,经销商在放养x天后全部售出,当 时,经销商总获利的最大值为1800元,求a的值(总获利=日销售总额-收购成本-其他费用)25. 如图,在平面直角坐标系中,已知矩形 的三个顶点 ,以A为顶点的抛物线 过点C,动点P从点A出发,以每秒 个单位的速度沿线段 向点D运动,运动时间为t秒,过点P作 轴交抛物线于点M,交 于点N.
(1)、求反比例函数的解析式和点B坐标;(2)、根据图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)、若C是双曲线上的动点,D是x轴上的动点,是否存在这样的点C和点D,使以A、B、C、D为顶点的四边形是平行四边形?若存在,求出C、D坐标;若不存在,请说明理由.24. 某水产经销商从批发市场以30元每千克的价格收购了1000千克的虾,了解到市场价在30元每千克的基础上一个月内会以每天0.5元每千克的价格上涨,经销商打算先在塘里放养几天后再出售(但不超过一个月).假设放养期间虾的个体质量保持不变,但每天有10千克的虾死去.死去的虾会在当天以20元每千克的价格售出.(1)、若放养8天后出售,则活虾的市场价为每千克元.(2)、若放养x天后将活虾一次性售出,总共获得的销售总额y元,求y与x的函数关系式;(3)、若放养期间,每天会有各种其他的各种费用支出为a元,经销商在放养x天后全部售出,当 时,经销商总获利的最大值为1800元,求a的值(总获利=日销售总额-收购成本-其他费用)25. 如图,在平面直角坐标系中,已知矩形 的三个顶点 ,以A为顶点的抛物线 过点C,动点P从点A出发,以每秒 个单位的速度沿线段 向点D运动,运动时间为t秒,过点P作 轴交抛物线于点M,交 于点N. (1)、直接写出点A的坐标,并求出抛物线的解析式;(2)、当t为何值时, 的面积最大?最大值为多少?(3)、点Q从点C出发,以每秒1个单位的速度沿线段 向点D运动,连接 .当t为何值时, 为等腰三角形?求出所有符合条件的t的值;(4)、在(3)的条件下,求当t为何值时,在线段 上存在点H,使以C,Q,N,H为顶点的四边形为菱形?
(1)、直接写出点A的坐标,并求出抛物线的解析式;(2)、当t为何值时, 的面积最大?最大值为多少?(3)、点Q从点C出发,以每秒1个单位的速度沿线段 向点D运动,连接 .当t为何值时, 为等腰三角形?求出所有符合条件的t的值;(4)、在(3)的条件下,求当t为何值时,在线段 上存在点H,使以C,Q,N,H为顶点的四边形为菱形?