湖北省武汉市2021年数学中考模拟试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 实数-2020的相反数是( )A、2020 B、-2020 C、2021 D、-20212. 下列x的值能使二次根式 有意义的是( )A、-2 B、-1 C、0 D、13. 下列事件中,是必然事件的是( )A、从一个只有红球的盒子里摸出一个球是红球 B、买一张电影票,座位号是5的倍数 C、掷一枚质地均匀的硬币,正面向上 D、走过一个红绿灯路口时,前方正好是红灯4. 下列微信表情图标属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图是一个空心圆柱体,其俯视图是( )
5. 如图是一个空心圆柱体,其俯视图是( )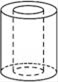 A、
A、 B、
B、 C、
C、 D、
D、 6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 若两个点(x1 , ﹣2),(x2 , 4)均在反比例函数y= 的图象上,且x1>x2 , 则k的值可以是( )A、4 B、3 C、2 D、18. 某快递公司每天上午 为集中件和派件时段,甲仓库用来揽收快件,乙仓库用来派发件快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:① 分钟后,甲仓库内快件数量为 件;②乙仓库每分钟派送快件数量为 件:③ 时,甲仓库内快件数为 件;④ 时,两仓库快递件数相同( )
6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 若两个点(x1 , ﹣2),(x2 , 4)均在反比例函数y= 的图象上,且x1>x2 , 则k的值可以是( )A、4 B、3 C、2 D、18. 某快递公司每天上午 为集中件和派件时段,甲仓库用来揽收快件,乙仓库用来派发件快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:① 分钟后,甲仓库内快件数量为 件;②乙仓库每分钟派送快件数量为 件:③ 时,甲仓库内快件数为 件;④ 时,两仓库快递件数相同( ) A、 个 B、 个 C、 个 D、 个9. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
A、 个 B、 个 C、 个 D、 个9. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )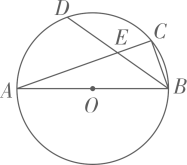 A、 B、 C、 D、10. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图形有10个正三角形,…依此规律,若第n个图案有2020个三角形,则 ( )
A、 B、 C、 D、10. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图形有10个正三角形,…依此规律,若第n个图案有2020个三角形,则 ( ) A、670 B、672 C、673 D、676
A、670 B、672 C、673 D、676二、填空题
-
11. 化简二次根式 的结果是.12. 热爱劳动,劳动最美!某合作学习小组6名同学一周居家劳动的时间(单位:h),分别为:4,3,3,5,5,6.这组数据的中位数是.13. 计算: .14. 在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD=.
 15. 抛物线 与x轴有两个交点,且交点位于y轴两侧,则下列关于这个二次函数的说法正确的有.(填序号)
15. 抛物线 与x轴有两个交点,且交点位于y轴两侧,则下列关于这个二次函数的说法正确的有.(填序号)① ;②若 ,则当 时,y随x的增大而增大;③ ;④一元二次方程 的两根异号.
16. 如图,折叠矩形纸片 ,使点D落在 边的点M处, 为折痕, , .设 的长为t,用含有t的式子表示四边形 的面积是.
三、解答题
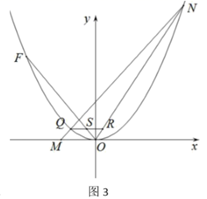
-
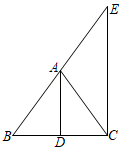
17. 计算: .18. 如图,已知 于点 , 是延长线 上一点,且 于点 ,若 .求证: 平分 .
 19. 为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100~90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如图统计图,请你根据统计图解答以下问题:
19. 为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100~90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如图统计图,请你根据统计图解答以下问题: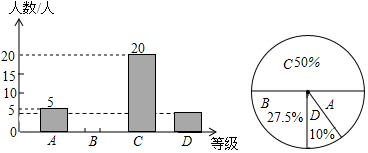 (1)、这次随机抽取的学生共有人?在如图扇形统计图中A等级所对应的圆心角度数为度.(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?20. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形, 的顶点均在格点上,点 的坐标为 .
(1)、这次随机抽取的学生共有人?在如图扇形统计图中A等级所对应的圆心角度数为度.(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?20. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形, 的顶点均在格点上,点 的坐标为 .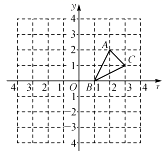
( 1 )画出 关于 轴对称的 ,并写出 点的坐标;
( 2 )画出将 绕原点 按逆时针旋转 所得的 ,并写出 点的坐标.
21. 如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.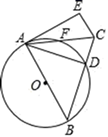 (1)、求证:AD=AE.(2)、若AB=10,sin∠DAC= 求AD的长.22. 某超市购进一批时令水果,成本为10 元/千克,根据市场调研发现,这种水果在未来30天的销售单价m(元/千克)与时间x(天)之间的函数关系式为 ( 且 为整数),且其日销售量y (千克)与时间x(天)之间的函数关系如图所示:
(1)、求证:AD=AE.(2)、若AB=10,sin∠DAC= 求AD的长.22. 某超市购进一批时令水果,成本为10 元/千克,根据市场调研发现,这种水果在未来30天的销售单价m(元/千克)与时间x(天)之间的函数关系式为 ( 且 为整数),且其日销售量y (千克)与时间x(天)之间的函数关系如图所示: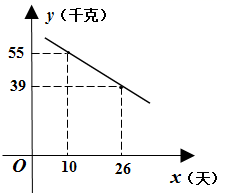 (1)、求每天销售这种水果的利润W(元)与x(天)之间的函数关系式;(2)、问哪一天销售这种水果的利润最大?最大日销售利润为多少?23. 在平行四边形ABCD中,点E、F分别在边AB、BC上,DE、AF交于点M.
(1)、求每天销售这种水果的利润W(元)与x(天)之间的函数关系式;(2)、问哪一天销售这种水果的利润最大?最大日销售利润为多少?23. 在平行四边形ABCD中,点E、F分别在边AB、BC上,DE、AF交于点M. (1)、如图1,E为AB的中点,AF⊥BC交BC于点F,过点E作EN⊥AF交AF于点N, ,直接写出 的值是;(2)、如图2,∠B=90°,∠ADE=∠BAF,求证:△AEM∽△AFB;(3)、如图3,∠B=60°,AB=AD,∠ADE=∠BAF,求证: .24. 如图1,直线 与 轴, 轴分别交于点 ,点 ,抛物线 经过点 ,点 和点 ,并与直线 交于另一点 .
(1)、如图1,E为AB的中点,AF⊥BC交BC于点F,过点E作EN⊥AF交AF于点N, ,直接写出 的值是;(2)、如图2,∠B=90°,∠ADE=∠BAF,求证:△AEM∽△AFB;(3)、如图3,∠B=60°,AB=AD,∠ADE=∠BAF,求证: .24. 如图1,直线 与 轴, 轴分别交于点 ,点 ,抛物线 经过点 ,点 和点 ,并与直线 交于另一点 .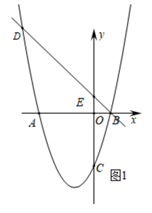 (1)、求抛物线 的解析式;(2)、如图2,点 为 轴上一动点,连接 ,当 时,求点 的坐标;
(1)、求抛物线 的解析式;(2)、如图2,点 为 轴上一动点,连接 ,当 时,求点 的坐标;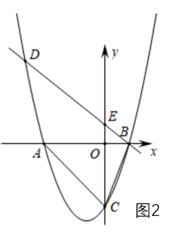 (3)、如图3,将抛物线 平移,使其顶点是坐标原点 ,得到抛物线 ;将直线 向下平移经过坐标原点 ,交抛物线 于另一点 .点 ,点 是 上且位于第一象限内一动点, 交 于 点, 轴分别交 于 ,试说明: 与 存在一个确定的数量关系.
(3)、如图3,将抛物线 平移,使其顶点是坐标原点 ,得到抛物线 ;将直线 向下平移经过坐标原点 ,交抛物线 于另一点 .点 ,点 是 上且位于第一象限内一动点, 交 于 点, 轴分别交 于 ,试说明: 与 存在一个确定的数量关系.