河南省洛阳市汝阳县2021年数学中考一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 抛物线y＝（x﹣2）²+3的对称轴是（）

A、直线x＝﹣3 B、直线x＝3 C、直线x＝2 D、直线x＝﹣2

查看试题解析
2. 为了解汝阳县汽车站今年春节期间每天乘车人数这个问题，随机抽查了其中七天的乘车人数，被抽查的这七天的乘车人数是这个问题的（）.

A、总体 B、个体 C、样本 D、以上都不对

查看试题解析
3. 如图，被阴影覆盖的可能是下面哪一个数（）

A、﹣ $\sqrt{3}$ B、 $\sqrt{7}$ C、 $\sqrt{11}$ D、以上都不对

查看试题解析
4. 关于x的一元二次方程x²+4x+k＝0有两个相等的实数根，则k的值为（）

A、k＝4 B、k＝﹣4 C、k≥﹣4 D、k≥4

查看试题解析
5. 李红同学遇到了这样一道题： $\sqrt{3}$ tan(α+20°)=1，你猜想锐角α的度数应是（）

A、40° B、30° C、20° D、10°

查看试题解析
6. 若AB是⊙O的直径，∠ACB＝90°，则点C一定在（）

A、⊙O内 B、⊙O外 C、⊙O上 D、⊙O内或⊙O上

查看试题解析
7. 已知二次函数y=ax²+bx+c，且a＜0，a-b+c＞0，则一定有（）

A、 $b^{2} - 4 ac > 0$ B、 $b^{2} - 4 ac = 0$ C、 $b^{2} - 4 ac < 0$ D、 $b^{2} - 4 ac \leq 0$

查看试题解析
8. 某市公园的东、西、南、北方向上各有一个入口，周末佳佳和琪琪随机从一个入口进入该公园游玩，则佳佳和琪琪恰好从同一个入口进入该公园的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{16}$

查看试题解析
9. 如图，已知⊙O中∠AOB度数为100°，C是圆周上的一点，则∠ACB的度数为（）

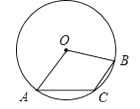A、130° B、100° C、80° D、50°

查看试题解析
10. 已知二次函数y=ax²+bx+c的图象如图所示，有以下结论：
①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④9a﹣3b+c＜0；⑤c﹣a＞1.其中所有正确结论的序号是(　　)

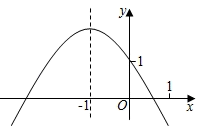A、①② B、①③④ C、①②③④ D、①②③④⑤

查看试题解析

二、填空题

11. 圆锥的底面半径为5cm，圆锥母线长为13cm，则圆锥的侧面积为cm²（结果保留π）.

查看试题解析
12. 一个不透明的盒子里有红色、黄色、白色小球共80个.它们除颜色外均相同，小文将这些小球摇匀后从中随机摸出一个记下颜色，再把它放回盒中，不断重复，多次试验后他发现摸到红色、黄色小球的频率依次为30%和40%.由此可估计盒中大约有白球个.

查看试题解析
13. 如图，在⊙E中，弦AB与CD相交于坐标原点O，已知B（0，﹣3），C（﹣2，0），D（6，0），则点A的坐标是.

查看试题解析
14. 如图， $△ A B C$ 中， $A B = A C = 10$ ， $\tan A = 2$ ， $B E ⊥ A C$ 于点 $E$ ， $D$ 是线段 $B E$ 上的一个动点，则 $C D + \frac{\sqrt{5}}{5} B D$ 的最小值是.

查看试题解析

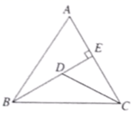
三、解答题

15. 已知实数a是一元二次方程x²－2016x＋1＝0的根，求代数式a²－2015a－ $\frac{a^{2} + 1}{2016}$ 的值.

查看试题解析
16. 先化简，再求代数式 $\frac{a - 2}{a + 1}$ ÷（a﹣1﹣ $\frac{3}{a + 1}$ ）的值，其中a＝2sin60°﹣2tan45°.

查看试题解析
17. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE．

(1)、求证：AE是⊙O的切线；

(2)、如果AB=4，AE=2，求⊙O的半径．

查看试题解析
18. 已知m，n是方程x²﹣2x﹣1＝0的两个根，是否存在实数a使﹣（m+n）（7m²﹣14m+a）（3n²﹣6n﹣7）的值等于8？若存在，求出a的值；若不存在，请说明理由.

查看试题解析

19. 某校为了解学生对“防溺水”安全知识的掌握情况，从全校1500名学生中随机抽取部分学生进行测试，并将测试成绩（百分制，得分均为整数）进行统计分析，绘制了不完整的频数表和频数直方图.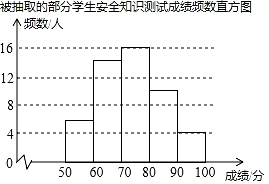

组别	成绩x（分）	频数（人）	频率
A组	50≤x＜60	6	0.12
B组	60≤x＜70	a	0.28
C组	70≤x＜80	16	0.32
D组	80≤x＜90	10	0.20
E组	90≤x≤100	4	0.08

由图表中给出的信息回答下列问题：

(1)、表中的a＝；抽取部分学生的成绩的中位数在组；

(2)、把如图的频数直方图补充完整；

(3)、如果成绩达到80分以上（包括80分）为优秀，请估计该校1500名学生中成绩优秀的人数.

查看试题解析

20. 某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．
根据图象提供的信息，解答下列问题：

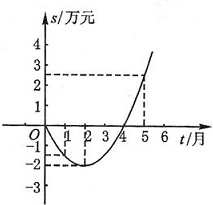(1)、由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；

(2)、求截止到几月末公司累积利润可达到30万元；

(3)、求第8个月公司所获利润为多少万元?

查看试题解析
21. 如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板长 $A B = 120 mm$ ，支撑板长 $C D = 80 mm$ ，底座长 $D E = 90 mm$ ，托板 $A B$ 固定在支撑板顶端点C处，且 $C B = 40 mm$ ，托板 $A B$ 可绕点 $C$ 转动，支撑板 $C D$ 可绕点D转动．（结果保留小数点后一位）

(1)、若 $∠ D C B = 80^{°}$ ， $∠ C D E = 60^{°}$ ，求点A到直线 $D E$ 的距离；

(2)、为了观看舒适，在（1）的情况下，把 $A B$ 绕点C逆时针旋转 $10^{\circ}$ 后，再将 $C D$ 绕点D顺时针旋转，使点B落在直线 $D E$ 上即可，求 $C D$ 旋转的角度．（参考数据： $\sin 40^{°} \approx 0.643 ， \cos 40^{°} \approx 0.766$ ， $\tan 40^{°} \approx 0.839$ ， $\sin {26.6}^{\circ} \approx 0.448$ ， $\cos {26.6}^{°} \approx 0.894 ， \tan {26.6}^{°} \approx 0.500$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
22. 已知二次函数y₁=a（x﹣2）²+k中，函数y₁与自变量x的部分对应值如表：
x
…
1
2
3
4
…
y
…
2
1
2
5
…

(1)、求该二次函数的表达式；

(2)、将该函数的图象向左平移2个单位长度，得到二次函数y₂的图象，分别在y₁、y₂的图象上取点A（m，n₁）B（m+1，n₂），试比较n₁与n₂的大小．

查看试题解析
23. 如图

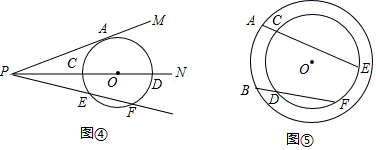
（问题探究）

已知：如图①所示，∠MPN的顶点为P，⊙O的圆心O从顶点P出发，沿着PN方向平移.

(1)、如图②所示，当⊙O分别与射线PM，PN相交于A、B、C、D四个点，连接AC、BD，可以证得△PAC∽△ ，从而可以得到：PA•PB＝PC•PD.

(2)、如图③所示，当⊙O与射线PM相切于点A，与射线PN相交于C、D两个点.求证：PA²＝PC•PD.

(3)、（简单应用）
如图④所示，（2）中条件不变，经过点P的另一条射线与⊙O相交于E、F两点.利用上述（1），（2）两问的结论，直接写出线段PA与PE、PF之间的数量关系；当PA＝4 $\sqrt{3}$ ，EF＝2，则PE＝.

(4)、（拓展延伸）
如图⑤所示，在以O为圆心的两个同心圆中，A、B是大⊙O上的任意两点，经过A、B两点作线段，分别交小⊙O于C、E、D、F四个点.求证：AC•AE＝BD•BF.（友情提醒：可直接运用本题上面所得到的相关结论）

查看试题解析

x	…	1	2	3	4	…
y	…	2	1	2	5	…