2021年河南省中考数学线上公益大模考诊断试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )
A、﹣ B、 C、﹣5 D、52. 2020年,我国国内生产总值达到101.6万亿元,数据“101.6万亿”用科学记数法表示为( )A、 10.16×1013 B、0.1016×1015 C、1.016×1012 D、1.016×10143. 将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=65°,则∠2的度数为( )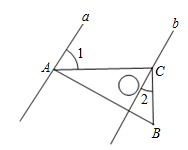 A、75° B、65° C、35° D、25°4. 下列计算正确的是( )A、a2+a3=a5 B、(﹣2a)3=﹣6a3 C、a3•a5=a8 D、(a﹣2)2=a2﹣45. 如图是由7个相同的小正方体搭成的几何体,在标号为①的小正方体上方添加一个小正方体后,所得几何体的三视图与原几何体的三视图相比没有发生变化的是( )
A、75° B、65° C、35° D、25°4. 下列计算正确的是( )A、a2+a3=a5 B、(﹣2a)3=﹣6a3 C、a3•a5=a8 D、(a﹣2)2=a2﹣45. 如图是由7个相同的小正方体搭成的几何体,在标号为①的小正方体上方添加一个小正方体后,所得几何体的三视图与原几何体的三视图相比没有发生变化的是( ) A、主视图和俯视图 B、主视图和左视图 C、左视图和俯视图 D、主视图、左视图和俯视图6. 若点A(﹣2,y1),B(﹣1,y2)在反比例函数y= 的图象上,则y1﹣y2的值为( )A、负数 B、0 C、正数 D、无法确定7. 下列说法正确的是( )A、了解河南省初中生身高情况适宜全面调查 B、甲,乙两名射击运动员5次射击成绩的方差分别为s甲2=1.2,s乙2=2,说明甲的射击成绩比乙的射击成绩稳定 C、同旁内角互补是必然事件 D、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次8. 关于x的一元二次方程x(x+1)﹣3=mx的根的情况是( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断9. 如图,在▱ABCD中,AB=2 ,点E为AD的中点,按以下步骤作图:①以点E为圆心,EA长为半径作弧,交AB于点F;②再分别以点A和点F为圆心,大于 AF的长为半径作弧,两弧相交于点M;③作直线EM交AB于点N,连接CE.若∠ADC=135°,DE=2,则CE的长为( )
A、主视图和俯视图 B、主视图和左视图 C、左视图和俯视图 D、主视图、左视图和俯视图6. 若点A(﹣2,y1),B(﹣1,y2)在反比例函数y= 的图象上,则y1﹣y2的值为( )A、负数 B、0 C、正数 D、无法确定7. 下列说法正确的是( )A、了解河南省初中生身高情况适宜全面调查 B、甲,乙两名射击运动员5次射击成绩的方差分别为s甲2=1.2,s乙2=2,说明甲的射击成绩比乙的射击成绩稳定 C、同旁内角互补是必然事件 D、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次8. 关于x的一元二次方程x(x+1)﹣3=mx的根的情况是( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断9. 如图,在▱ABCD中,AB=2 ,点E为AD的中点,按以下步骤作图:①以点E为圆心,EA长为半径作弧,交AB于点F;②再分别以点A和点F为圆心,大于 AF的长为半径作弧,两弧相交于点M;③作直线EM交AB于点N,连接CE.若∠ADC=135°,DE=2,则CE的长为( )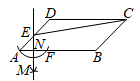 A、2 B、4 C、2 D、10. 如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(4,0),以AB为边构造菱形ABEF,将菱形ABEF与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转45°,则第164次旋转结束时,点 的坐标为( )
A、2 B、4 C、2 D、10. 如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(4,0),以AB为边构造菱形ABEF,将菱形ABEF与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转45°,则第164次旋转结束时,点 的坐标为( ) A、(﹣4,4 ) B、(﹣4,﹣4 ) C、(4 ,﹣4) D、(﹣4 ,﹣4)
A、(﹣4,4 ) B、(﹣4,﹣4 ) C、(4 ,﹣4) D、(﹣4 ,﹣4)二、填空题
-
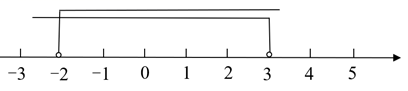
11. 若 都是无理数,且 ,则 的值分别是(填一组满足条件的值).12. 关于 的不等式组 的解集在数轴上如图表示,则 的值为.
 13. 某社团中有三名男生和一名女生,该社团将随机选派两名同学作为代表参加市级比赛,恰好选中一男一女的概率是.14. 如图,在扇形BCD中,∠BCD=150°,以点B为圆心,BC长为半径画弧交 于点A,连接AC,若BC=4,则图中阴影部分的面积为.
13. 某社团中有三名男生和一名女生,该社团将随机选派两名同学作为代表参加市级比赛,恰好选中一男一女的概率是.14. 如图,在扇形BCD中,∠BCD=150°,以点B为圆心,BC长为半径画弧交 于点A,连接AC,若BC=4,则图中阴影部分的面积为.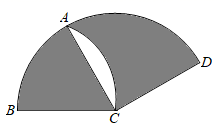 15. 如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN=.
15. 如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN=.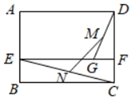
三、解答题
-
16. 先化简,再求值:( ﹣1)÷ ,其中a= +2.17. 某校为了解七、八年级学生对“文明知识礼仪”的掌握情况,从七、八年级各随机抽取了25名学生进行相关测试,并对成绩进行整理、描述和分析,部分信息如下:

c.八年级D组测试成绩数据为:90,90,91,92,93,94,94;
d.七、八年级被抽取学生测试成绩的平均数、中位数如下表所示:
平均数
中位数
七年级
87.36
87
八年级
91.36
a
根据所给信息,解答下列问题:
(1)、根据统计图,对比两个年级成绩在90分以上(含90分)的百分比,七年级比八年级;(填“大”或“小”)(2)、表中a的值为;(3)、小华的测试成绩为89分,他的成绩在本年级参加测试的学生中处于中上游,请判断小华是 ▲ 年级的学生,并说明理由;(4)、学校决定对本次测试成绩优异的学生进行奖励,老师从七、八年级各抽取了4名同学的成绩记录如下表:七年级
八年级
学生代码
A
B
C
D
E
F
G
H
成绩
98
93
90
95
87
96

其中有两名同学的成绩被墨汁污染了,但老师说七年级和八年级被抽取的这4名同学中各有2名同学可以获得奖励,于是小明说G和H两名同学中只有一名同学可以获得奖励.请问小明的说法是否正确?并说明理由.
18. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部,其公园南山门被誉为“亚洲第一门”,学完了三角函数知识后,某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,小组在测量仰角以及两点间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如表:课题
测量南山门最高点的高度
实物图

成员
组长:xxx
组员:xxx,xxx,xxx
测量工具
卷尺、测角仪……
测量示意图
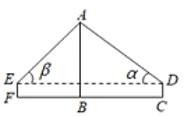
说明:AB表示南山门最高点到地面的竖直距离.测角仪的高度CD-EF-1.5m点C.F与点B在同一直线上,点C.F之间的距离可直接测将,且点A、B.C.D.E、F在同一平面内.
测量数据
第一次
第二次
平均值
35.95°
36.05°
36°
45.09°
44.91°
45°
79.58m
79.62m
79.6m
……
……
(1)、请帮助该小组的同学根据上表中的测量数据,求南山门最高点的高度AB.(结果精确到0.1m,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73, ≈1.41)(2)、该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)19. 为提升校园体育运动多样性,助力师生“阳光运动”,某校决定采购一批排球和足球,小明在某体育用品商店咨询了排球和足球的售价具体信息:购买2个排球和3个足球共需460元,购买12个排球所需费用与购买5个足球所需费用相同.(1)、求排球和足球的售价分别是多少元?(2)、若该校计划购进排球和足球共100个,其中排球的数量不超过足球的3倍,请设计出最省钱的购买方案,并说明理由.20. 如图,抛物线y=ax2﹣4x+c经过点A(2,﹣2),且当x=1时,函数y有最小值.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.) (1)、求抛物线的解析式;(2)、点B的坐标为(﹣3,﹣4),点B关于原点的对称点为B',点C是抛物线对称轴上一动点,若抛物线在直线BB'下方的部分与直线BC有公共点,求点C纵坐标yc的取值范围.21. 若一直线与圆相交,过交点作圆的切线,则此切线与直线的交角中的任意一个称为直线和圆的交角,其中所夹弧为劣弧的角为劣交角,所夹弧为优弧的角为优交角.直线和圆的交角有以下性质:直线和圆的交角等于所夹弧所对的圆周角.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)
(1)、求抛物线的解析式;(2)、点B的坐标为(﹣3,﹣4),点B关于原点的对称点为B',点C是抛物线对称轴上一动点,若抛物线在直线BB'下方的部分与直线BC有公共点,求点C纵坐标yc的取值范围.21. 若一直线与圆相交,过交点作圆的切线,则此切线与直线的交角中的任意一个称为直线和圆的交角,其中所夹弧为劣弧的角为劣交角,所夹弧为优弧的角为优交角.直线和圆的交角有以下性质:直线和圆的交角等于所夹弧所对的圆周角.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)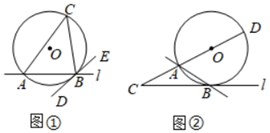 (1)、为了说明直线和圆的交角性质的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程(只证明劣交角即可).
(1)、为了说明直线和圆的交角性质的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程(只证明劣交角即可).已知:如图①,直线l与⊙O相交于点A、B,过点B作.
求证:∠ABD=.
(2)、如图②,直线l与⊙O相交于点A、B,AD为⊙O的直径,BC切⊙O于点B,交DA的延长线于点C,若AD=BC,AC=2,求⊙O的半径.22. 如图①,在△ABC中,∠ACB=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED并延长交CG于点F,连接AF.设A、E两点间的距离为xcm,E、F两点间的距离为ycm.小亮根据学习函数的经验,对因变量y随自变量x变化而变化的规律进行了探究.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)下面是小亮的探究过程,请补充完整: (1)、列表:如表的已知数据是根据A、E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
(1)、列表:如表的已知数据是根据A、E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:x/cm
0
1
2
3
4
5
6
y/cm
9.49
7.62
5.83
3.16
3.16
4.24
请你通过计算补全表格;
(2)、描点、连线:在平面直角坐标系xOy中,描出剩余的点(x,y),并画出函数y关于x的图象;(3)、根据函数图象,当E、F两点间的距离y最小时,A、E两点间的距离约为cm;(4)、解决问题:当EF﹣AE=2时,BE的长度大约是cm.(结果保留1位小数)23. 如图①,△ABC为直角三角形,∠ACB=90°,∠BAC=30°,点D在AB边上,过点D作DE⊥AC于点E,取BC边的中点F,连接DF并延长到点G,使FG=DF,连接CG.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.) (1)、问题发现:
(1)、问题发现:填空:CE与CG的数量关系是 , 直线CE与CG所夹的锐角的度数为.
(2)、探究证明:将△ADE绕点A逆时针旋转,(1)中的结论是否仍然成立,若成立,请仅就图②所示情况给出证明,若不成立,请说明理由;
(3)、问题解决:若AB=4,AD=3,将△ADE由图①位置绕点A逆时针旋转α(0°<α<180°),当△ACE是直角三角形时,请直接写出CG的值.