河南省2021年九年级第四届名校联盟考数学试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. -2021的绝对值是( )A、-2021 B、2021 C、 D、2. 植物学家在厄瓜多尔意外地发现了一种兰花新物种,是兰花物种中最小的一种,花瓣直径仅2.1毫米,把2.1毫米用科学记数法表示为 米,则 的值为( )A、-4 B、-3 C、-2 D、-13. 下列立体图形的主视图与左视图相同是( )
 A、①②③ B、②③ C、①②④ D、①②③④4. 下列各式计算正确的是( )A、 B、 C、 D、5. 如图, 是 的外角, , ,则 的度数为( )
A、①②③ B、②③ C、①②④ D、①②③④4. 下列各式计算正确的是( )A、 B、 C、 D、5. 如图, 是 的外角, , ,则 的度数为( )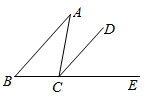 A、 B、 C、 D、6. 某学校对学生的期末操行评语成绩按班委评分、任课教师评分、家长评分三方面确定成绩(评分满分均为100分),若三方面依次按2:5:3确定成绩,且某同学所评的得分依次为90分、92分、91分,则该同学评分的最后得分是( )A、91分 B、91.3分 C、91.2分 D、91.1分7. 将4个数 、 、 、 排成2行、2列,两边各加一条竖直线记成 ,定义 .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根8. 如图, 的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A、 B、 C、 D、6. 某学校对学生的期末操行评语成绩按班委评分、任课教师评分、家长评分三方面确定成绩(评分满分均为100分),若三方面依次按2:5:3确定成绩,且某同学所评的得分依次为90分、92分、91分,则该同学评分的最后得分是( )A、91分 B、91.3分 C、91.2分 D、91.1分7. 将4个数 、 、 、 排成2行、2列,两边各加一条竖直线记成 ,定义 .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根8. 如图, 的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( ) A、1.5 B、2 C、2.5 D、39. 在 中 , ,分别以点 、 为圆心,大于 的长为半径作弧,两弧相交于点 、 .作直线 ,分别交 、 于点 、 ,连接 ,则 的周长为( )
A、1.5 B、2 C、2.5 D、39. 在 中 , ,分别以点 、 为圆心,大于 的长为半径作弧,两弧相交于点 、 .作直线 ,分别交 、 于点 、 ,连接 ,则 的周长为( )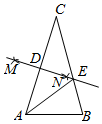 A、 B、 C、 D、10. 某同学在平面直角坐标系内设计了一个动点运动的编程.若一个动点从点 出发,沿 …运动,则点 的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、10. 某同学在平面直角坐标系内设计了一个动点运动的编程.若一个动点从点 出发,沿 …运动,则点 的坐标为( )A、 B、 C、 D、二、填空题
-
11. 计算: .12. 不等式组 的解集为.13. 在一个不透明的袋子里,放着标有数字2、5、7、8的四个小球(除数字不同外,其余都相同),在看不见的情况下随机摸出2个球,则摸出的两个球上的数字的和不小于10的概率是.14. 如图,在 中, , ,以 的中点 为圆心, 为半径作半圆.若 , 与 分别交半圆于点 、 ,则图中阴影部分的面积是.
 15. 如图,在周长为16,面积为6的矩形纸片 中, 是 的中点. 是 上一动点,将 沿直线 折叠,点 落在点 处.在 上任取一点 ,连接 , ,则 的最小值为.
15. 如图,在周长为16,面积为6的矩形纸片 中, 是 的中点. 是 上一动点,将 沿直线 折叠,点 落在点 处.在 上任取一点 ,连接 , ,则 的最小值为.
三、解答题
-
16. 先化简,再求值: .其中 , .17. 如图, 是 的直径, 是圆上不与点 、 重合的动点,连接 并延长 到点 ,使 ,连接 , 是 的中点,连接 、 、 .
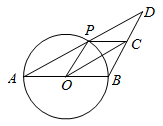 (1)、求证: .(2)、填空:
(1)、求证: .(2)、填空:①若 ,当 时,四边形 是菱形;
②当 时,四边形 是正方形.
18. 为了了解中学生对父母的关心程度,某校九年级兴趣小组利用课外活动时间随机调查了某市若干名学生对父母关心程度的情况( .给父母送自制的生日礼物; .陪父母聊天; .主动帮父母做家务; .知道母亲或父亲某个人的生日; .知道母亲和父亲的生日),并将调查结果绘制成条形统计图(如图1)和扇形统计图(如图2)(不完整).请你根据图中提供的信息,解答下列问题: (1)、此次调查的学生有人.(2)、将图1补充完整.(3)、在扇形统计图中, 部分所对应的圆心角的度数是.(4)、根据抽样调查结果,请你估计该市90000名中学生中主动帮父母做家务的有多少人?19. 如图,某公园有一小亭 ,它周围350米内是文物保护区.某勘探队员在公园由西向东行走,在 处测得小亭 在北偏东 的方向上,若勘探队员行走的速度是每分钟60米,从点 走到点 需要20分钟,此时测得小亭 在北偏西 的方向上.若该公园打算沿射线 的方向修一条笔直的小路,则此小路是否会通过文物保护区?请说明理由.(结果保留整数.参考数据: , , , )
(1)、此次调查的学生有人.(2)、将图1补充完整.(3)、在扇形统计图中, 部分所对应的圆心角的度数是.(4)、根据抽样调查结果,请你估计该市90000名中学生中主动帮父母做家务的有多少人?19. 如图,某公园有一小亭 ,它周围350米内是文物保护区.某勘探队员在公园由西向东行走,在 处测得小亭 在北偏东 的方向上,若勘探队员行走的速度是每分钟60米,从点 走到点 需要20分钟,此时测得小亭 在北偏西 的方向上.若该公园打算沿射线 的方向修一条笔直的小路,则此小路是否会通过文物保护区?请说明理由.(结果保留整数.参考数据: , , , ) 20. 如图,直线 与双曲线 相交于 、 两点,直线 与 轴相交于点 ,点 的坐标是 , , 为 轴正半轴上一点,且 .
20. 如图,直线 与双曲线 相交于 、 两点,直线 与 轴相交于点 ,点 的坐标是 , , 为 轴正半轴上一点,且 . (1)、双曲线 的解析式是 , 直线 的解析式是.(2)、求证: .(3)、当 时, 的取值范围是.21. 某超市每天能销售河南特产“伊川富硒小米”和“伊川贡小米”共21袋(5斤装),且“伊川富硒小米”6天销售的袋数与“伊川贡小米”8天销售的袋数相同.(1)、该超市每天销售“伊川富硒小米”和“伊川贡小米”各多少袋?(2)、“伊川富硒小米”每袋进价20元,售价25元;“伊川贡小米”每袋进价30元,售价33元.若超市打算购进“伊川富硒小米”和“伊川贡小米”共80袋,其中“伊川富硒小米”不超过40袋,要求这80袋小米全部销售完后的总利润不少于316元,则该超市如何购进这两种小米获利最大?最大利润是多少元?22. 如图
(1)、双曲线 的解析式是 , 直线 的解析式是.(2)、求证: .(3)、当 时, 的取值范围是.21. 某超市每天能销售河南特产“伊川富硒小米”和“伊川贡小米”共21袋(5斤装),且“伊川富硒小米”6天销售的袋数与“伊川贡小米”8天销售的袋数相同.(1)、该超市每天销售“伊川富硒小米”和“伊川贡小米”各多少袋?(2)、“伊川富硒小米”每袋进价20元,售价25元;“伊川贡小米”每袋进价30元,售价33元.若超市打算购进“伊川富硒小米”和“伊川贡小米”共80袋,其中“伊川富硒小米”不超过40袋,要求这80袋小米全部销售完后的总利润不少于316元,则该超市如何购进这两种小米获利最大?最大利润是多少元?22. 如图 (1)、观察猜想:如图1,在 中, , , 是 的平分线,以 为一边作正方形 ,点 与点 重合,则 .(2)、类比探究:在(1)的条件下,如果正方形 绕点 旋转,连接 、 、 ,(1)中的结论是否成立?请按图2加以证明.(3)、问题解决:当正方形 旋转到 、 、 三点共线时,请直接写出线段 的长.23. 已知抛物线 与 轴交于 、 两点(点 在点 的左边),与 轴交于点 ,抛物线的顶点为 ,连接 、 , .(1)、求抛物线的顶点 的坐标.(2)、求证: ,(3)、点 在抛物线上,点 在直线 上,是否存在点 、 使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、观察猜想:如图1,在 中, , , 是 的平分线,以 为一边作正方形 ,点 与点 重合,则 .(2)、类比探究:在(1)的条件下,如果正方形 绕点 旋转,连接 、 、 ,(1)中的结论是否成立?请按图2加以证明.(3)、问题解决:当正方形 旋转到 、 、 三点共线时,请直接写出线段 的长.23. 已知抛物线 与 轴交于 、 两点(点 在点 的左边),与 轴交于点 ,抛物线的顶点为 ,连接 、 , .(1)、求抛物线的顶点 的坐标.(2)、求证: ,(3)、点 在抛物线上,点 在直线 上,是否存在点 、 使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.