海南省乐东县2021年数学中考模拟试卷(一)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 有理数2021的相反数为( )A、2021 B、-2021 C、 D、2. 下列各选项的运算结果正确的是( )A、 B、 C、 D、3. 钓鱼岛自古以来就是中国的固有领土,在“百度”搜索引擎中输入“钓鱼岛最新消息”,能搜索到与之相关的结果个数约为4640000,这个数字用科学记数法表示为( )A、 B、 C、 D、4. 如图中几何体的左视图是( )
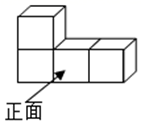 A、
A、 B、
B、 C、
C、 D、
D、 5. 在△ABC中,∠C=90°,AB=15,sinA= , 则BC等于( )A、45 B、5 C、 D、6. 如图所示的各图中,上方图形可看成由下方图形绕着一个顶点顺时针旋转90°而形成的是( )A、
5. 在△ABC中,∠C=90°,AB=15,sinA= , 则BC等于( )A、45 B、5 C、 D、6. 如图所示的各图中,上方图形可看成由下方图形绕着一个顶点顺时针旋转90°而形成的是( )A、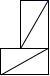 B、
B、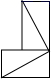 C、
C、 D、
D、 7. 从一副(54张)扑克牌中任意抽取一张,正好为K的概率为( )A、 B、 C、 D、8. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣9. 能判定 与 相似的条件是( )A、 B、 ,且 C、 且 D、 ,且10. 如图, 是 的外接圆,半径为 ,若 ,则 的度数为( )
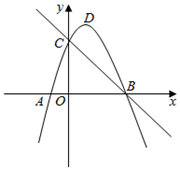
7. 从一副(54张)扑克牌中任意抽取一张,正好为K的概率为( )A、 B、 C、 D、8. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣9. 能判定 与 相似的条件是( )A、 B、 ,且 C、 且 D、 ,且10. 如图, 是 的外接圆,半径为 ,若 ,则 的度数为( )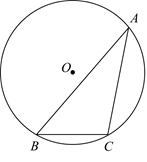 A、30° B、25° C、15° D、10°11. 经过两次连续降价,某药品销售单价由原来的60元降到42元,设该药品平均每次降价的百分率为x,根据题意可列方程是( )A、 B、 C、 D、12. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A、30° B、25° C、15° D、10°11. 经过两次连续降价,某药品销售单价由原来的60元降到42元,设该药品平均每次降价的百分率为x,根据题意可列方程是( )A、 B、 C、 D、12. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
13. 因式分解: .14. 若关于x的一元二次方程x2﹣4x﹣m=0有两个不相等的实数根,则实数m的取值范围是 .
15. 计算 的结果是.16. 把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,…,按此规律排列下去,则第n个图案中黑色三角形的个数为.
三、解答题
-
17.(1)、计算: .(2)、解不等式组 ,并写出它的最大负整数解.18. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?19. 农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
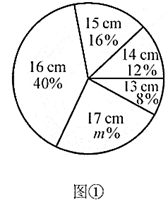
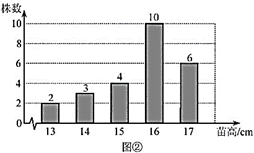
请根据相关信息,解答下列问题:
(Ⅰ)本次抽取的麦苗的株数为 ▲ ,图①中m的值为 ▲ ;
(Ⅱ)求统计的这组苗高数据的平均数、众数和中位数.
20. 如图,我国某海城有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西 方向,在港口B的北偏西 方向. (1)、直接写出: , .(2)、求货船与港口A之间的距离.(结果保留根号)
(1)、直接写出: , .(2)、求货船与港口A之间的距离.(结果保留根号)