贵州省毕节市织金县2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
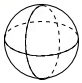
1. 2021的相反数的倒数是( )A、 B、﹣2021 C、±2021 D、﹣2. 下列计算:①(﹣1)0=﹣1;②(﹣2)﹣2= ;③用科学记数法表示﹣0.0000108=1.08×10﹣5.其中正确的有( )A、3个 B、2个 C、1个 D、0个3. 若 满足 则 的值是( )A、1 B、-1 C、2019 D、-20194. 下面四个几何体中,主视图为三角形的是( )A、
 B、
B、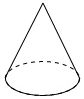 C、
C、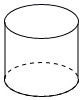 D、
D、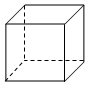 5. 下列图标中,既是轴对称图形又是中心对称图形的是( )A、
5. 下列图标中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、a3+a3=a6 B、(a3)2=a6 C、a6÷a2=a3 D、(ab)3=ab37. 若 = ,则 的值为( )A、 B、 C、 D、8. 如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )
6. 下列计算正确的是( )A、a3+a3=a6 B、(a3)2=a6 C、a6÷a2=a3 D、(ab)3=ab37. 若 = ,则 的值为( )A、 B、 C、 D、8. 如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )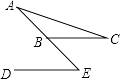 A、24° B、59° C、60° D、69°9. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )
A、24° B、59° C、60° D、69°9. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )成绩/分
84
88
92
96
100
人数/人
2
4
9
10
5
A、92分,96分 B、94分,96分 C、96分,96分 D、96分,100分10. 已知等腰三角形的一条腰长是15,底边长是18,则它底边上的高为( )A、9 B、12 C、15 D、1811. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )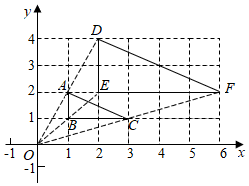 A、 B、2 C、4 D、212. 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A、 B、2 C、4 D、212. 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )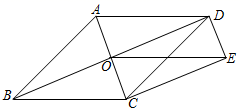 A、8 B、9 C、10 D、1213. 关于 的不等式组 ,有四个整数解,则 的取值范围是( )A、 B、 C、 D、14. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
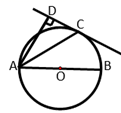
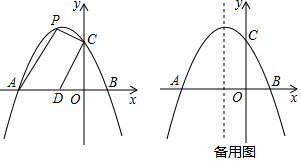
A、8 B、9 C、10 D、1213. 关于 的不等式组 ,有四个整数解,则 的取值范围是( )A、 B、 C、 D、14. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )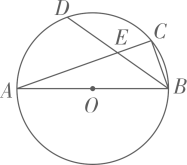 A、 B、 C、 D、15. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
A、 B、 C、 D、15. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
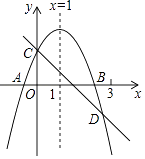 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
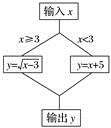
16. 分解因式y3﹣2y2+y=.17. 已知a,b是一个等腰三角形的两边长,且满足a2+b2-6a-8b+25=0,则这个等腰三角形的周长为.18. 某计算程序如图所示,当输入x= , 输出y=1.
 19. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是
19. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是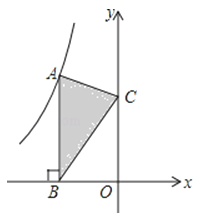 20. 设a= ,b= ,则a2020b2021的值是.
20. 设a= ,b= ,则a2020b2021的值是.三、解答题
-
21. 计算: .22. 先化简,( ﹣x﹣2)÷ ,然后从﹣2≤x≤2范围内选取一个合适的整数作为x的值代入求值.23. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
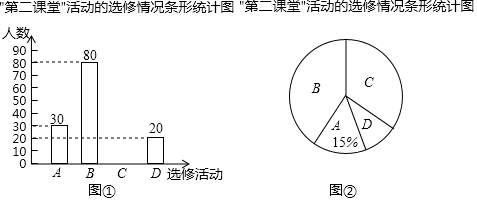
根据图中提供的信息,解答下列问题:
(1)、本次调查的学生共有人;在扇形统计图中,B所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.24. 某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.(1)、求甲、乙两种水果的单价分别是多少元?(2)、该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?25. 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.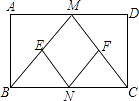 (1)、求证:△ABM≌△DCM;(2)、判断四边形MENF是什么特殊四边形,并证明你的结论.
(1)、求证:△ABM≌△DCM;(2)、判断四边形MENF是什么特殊四边形,并证明你的结论.