广西柳州市2021年数学中考一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 下面四个标志图是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面的几何体中,主(正)视图为三角形的是( )A、
2. 下面的几何体中,主(正)视图为三角形的是( )A、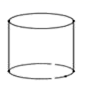 B、
B、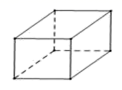 C、
C、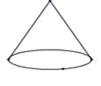 D、
D、 3. 上汽通用五菱2020年销量突破1600000辆,成为销量第一的民族品牌,该销量用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查5. 下列计算正确的是( ).A、 B、 C、 D、6. 下列关于方程 的结论正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、无实数根7. 如图, 、 、 是 上的三个点, ,则 的度数是( ).
3. 上汽通用五菱2020年销量突破1600000辆,成为销量第一的民族品牌,该销量用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查5. 下列计算正确的是( ).A、 B、 C、 D、6. 下列关于方程 的结论正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、无实数根7. 如图, 、 、 是 上的三个点, ,则 的度数是( ).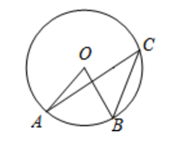 A、 B、 C、 D、8. 如图,在 中, , , ,则 ( )
A、 B、 C、 D、8. 如图,在 中, , , ,则 ( )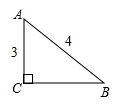 A、 B、 C、 D、9. 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( ).
A、 B、 C、 D、9. 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( ). A、1:2 B、1:4 C、2:1 D、4:110. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )
A、1:2 B、1:4 C、2:1 D、4:110. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )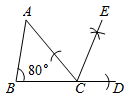 A、 B、 C、 D、11. 如图,有一圆弧形桥拱,拱形半径 ,桥拱跨度 ,则拱高 为( )
A、 B、 C、 D、11. 如图,有一圆弧形桥拱,拱形半径 ,桥拱跨度 ,则拱高 为( )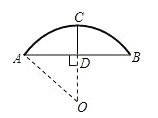 A、 B、 C、 D、12. 某企业1-6月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
A、 B、 C、 D、12. 某企业1-6月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )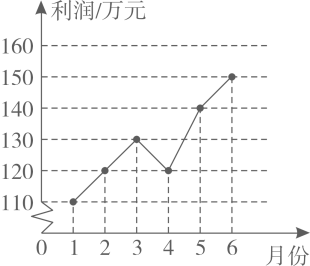 A、1-6月份利润的众数是130万元 B、1-6月份利润的中位数是130万元 C、1-6月份利润的平均数是130万元 D、1-6月份利润的极差是40万元
A、1-6月份利润的众数是130万元 B、1-6月份利润的中位数是130万元 C、1-6月份利润的平均数是130万元 D、1-6月份利润的极差是40万元二、填空题
-
13. 分解因式: = .14. 不等式组 的解为 .15. 如果m是关于x的方程x2+2x﹣3=0的一个根,则2m2+4m= .16. 一个扇形的半径为 ,圆心角为 ,则它的面积为 .17. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 .
 18. 如图,在矩形ABCD中,AD=3,M是CD上的一点,将△ADM沿直线AM对折得到△ANM , 若AN平分∠MAB , 则折痕AM的长为 .
18. 如图,在矩形ABCD中,AD=3,M是CD上的一点,将△ADM沿直线AM对折得到△ANM , 若AN平分∠MAB , 则折痕AM的长为 .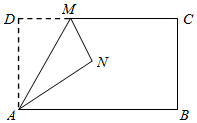
三、解答题
-
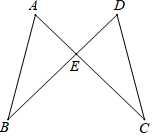
19. 计算:20. 如图,线段AC、BD相交于点E,AE=DE,BE=CE.求证:∠B=∠C.
 21. 如图,在 中, ,且点A的坐标是(2,0)
21. 如图,在 中, ,且点A的坐标是(2,0)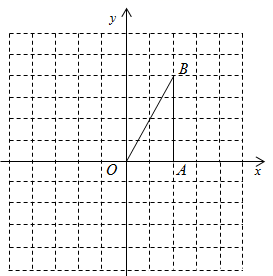 (1)、写出点B的坐标是;(2)、将点B向左平移4个单位长度,再向下平移1个单位长度,得到点C , 则点C的坐标为;(3)、点C与点D关于原点O对称,则点D的坐标为;(4)、将点A绕点O按逆时针方向旋转90°,得到点E , 则 的面积是 . (把答案填在相应的横线上,不用书写解答过程)22. 有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外无其他差别,现将它们背面朝上洗匀.(1)、随机抽取一张卡片,卡片上的数字是偶数的概率为.(2)、随机抽取一张卡片,然后放回洗匀,再随机抽取一张卡片,请用列表或画树状图的方法,求两次抽取的卡片上的数字和等于5的概率.23. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;(2)、销售单价为多少元时,该商品每天的销售利润最大?24. 如图,一次函数 与反比例函数 在第一象限的图象交于 , 两点.
(1)、写出点B的坐标是;(2)、将点B向左平移4个单位长度,再向下平移1个单位长度,得到点C , 则点C的坐标为;(3)、点C与点D关于原点O对称,则点D的坐标为;(4)、将点A绕点O按逆时针方向旋转90°,得到点E , 则 的面积是 . (把答案填在相应的横线上,不用书写解答过程)22. 有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外无其他差别,现将它们背面朝上洗匀.(1)、随机抽取一张卡片,卡片上的数字是偶数的概率为.(2)、随机抽取一张卡片,然后放回洗匀,再随机抽取一张卡片,请用列表或画树状图的方法,求两次抽取的卡片上的数字和等于5的概率.23. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;(2)、销售单价为多少元时,该商品每天的销售利润最大?24. 如图,一次函数 与反比例函数 在第一象限的图象交于 , 两点.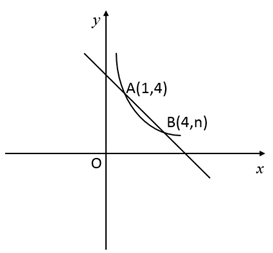 (1)、求出反比例函数的解析式和点B的坐标;(2)、根据图像直接写出 时x的取值范围;(3)、在y轴上找一点P , 使 的值最小,求出 的最小值和点P的坐标.25. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)、求出反比例函数的解析式和点B的坐标;(2)、根据图像直接写出 时x的取值范围;(3)、在y轴上找一点P , 使 的值最小,求出 的最小值和点P的坐标.25. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:AB•CP=BD•CD;(3)、当AB=5cm,AC=12cm时,求线段PC的长.26. 如图,已知直线y=﹣ x+2与x轴、y轴分别交于点B、C,抛物线y=﹣ +bx+c过点B、C,且与x轴交于另一个点A.
(1)、求证:PD是⊙O的切线;(2)、求证:AB•CP=BD•CD;(3)、当AB=5cm,AC=12cm时,求线段PC的长.26. 如图,已知直线y=﹣ x+2与x轴、y轴分别交于点B、C,抛物线y=﹣ +bx+c过点B、C,且与x轴交于另一个点A. (1)、求该抛物线的表达式;(2)、点M是线段BC上一点,过点M作直线l∥y轴交该抛物线于点N,当四边形OMNC是平行四边形时,求它的面积;(3)、联结AC,设点D是该抛物线上的一点,且满足∠DBA=∠CAO,求点D的坐标.
(1)、求该抛物线的表达式;(2)、点M是线段BC上一点,过点M作直线l∥y轴交该抛物线于点N,当四边形OMNC是平行四边形时,求它的面积;(3)、联结AC,设点D是该抛物线上的一点,且满足∠DBA=∠CAO,求点D的坐标.