广西河池市2021年数学中考一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 在下列各数中，比﹣2小的数是（）

A、﹣3 B、﹣2 C、0 D、1

查看试题解析
2. 计算（a²）³ ，正确结果是（　　）

A、a⁵ B、a⁶ C、a⁸ D、a⁹

查看试题解析
3. 抛物线y＝x²+4x+7的对称轴是（）

A、直线x＝4 B、直线x＝﹣4 C、直线x＝2 D、直线x＝﹣2

查看试题解析
4. 甲骨文是中国的一种古代文字，是汉字的早期形式.下列甲骨文中，是轴对称图形的是（）.

A、 B、 C、 D、

查看试题解析
5. 如图所示的几何体的主视图为（）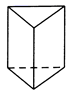

A、 B、 C、 D、

查看试题解析
6. 要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为4厘米，6厘米和9厘米，另一个三角形的最长边是18厘米，则它的最短边是（）

A、2厘米 B、4厘米 C、8厘米 D、12厘米

查看试题解析
7. 若mn＝﹣2，m﹣n＝3，则代数式m²n﹣mn²的值是（）

A、﹣6 B、﹣5 C、1 D、6

查看试题解析
8. 小明准备用40元钱购买作业本和签字笔.已知每个作业本6元，每支签字笔2.2元，小明买了7支签字笔，他最多还可以买的作业本个数为（）

A、5 B、4 C、3 D、2

查看试题解析
9. 如图， $⊙ O$ 中， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ， $∠ A B C = 70 °$ ．则 $∠ B O C$ 的度数为（）

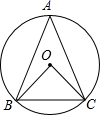A、100° B、90° C、80° D、70°

查看试题解析
10. 某语文教师调查了本班10名学生平均每天的课外阅读时间，统计结果如下表所示：

课外阅读时间（小时）

0.5

1

1.5

2

人数

2

3

4

1

那么这10名学生平均每天的课外阅读时间的平均数和众数分别是（）

A、1.2和1.5 B、1.2和4 C、1.25和1.5 D、1.25 和4

查看试题解析
11. 已知关于x的分式方程 $\frac{m}{x - 1} + 2 = - \frac{3}{1 - x}$ 的解为非负数，则正整数m的所有个数为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，有如下结论：① $a b c > 0$ ；② $2 a + b = 0$ ；③ $3 b - 2 c < 0$ ；④ $a m^{2} + b m \geq a + b$ （m为实数）.其中正确结论的个数是（）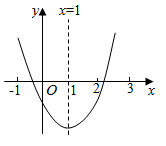

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 函数y= $\sqrt{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
14. 因式分解：a³－ab²＝.

查看试题解析
15. 盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字1，2，3，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为奇数的概率是.

查看试题解析
16. 如图， $⋄ A B C D$ 的对角线AC、BD相交于点O， $O E / / A B$ 交AD于点E，若OA=1， $Δ A O E$ 的周长等于5，则 $⋄ A B C D$ 的周长等于．

查看试题解析
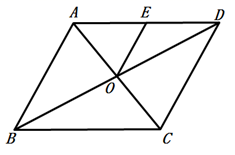17. 如图，点C、D分别是半圆AOB上的三等分点，若阴影部分的面积为 $\frac{3}{2} π$ ，则半圆的半径OA的长为．

查看试题解析
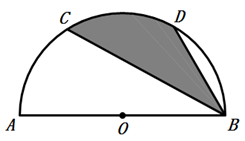18. 如图，已知矩形OABC的面积为 $\frac{100}{3}$ ，它的对角线OB与双曲线 $y = \frac{k}{x}$ 相交于点D，且OB：OD＝5：3，则k＝.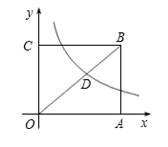

查看试题解析

三、解答题

19. 计算： $| - \sqrt{5} | - {(2021 - \sqrt{5})}^{0} + 2 \cos 60^{°} + {(\frac{1}{3})}^{0} - 1$ .

查看试题解析
20. 化简求值： $(2 x + 3) (2 x - 3) - {(x + 2)}^{2} + 4 (x + 3)$ ，其中 $x = \sqrt{2}$

查看试题解析
21. 如图，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠DCB，交对角线BD于点E，F.

(1)、若∠BCF=60°，求∠ABC的度数；

(2)、求证：BE=DF.

查看试题解析

22. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）.相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10.

七，八年级抽取的学生的竞赛成绩统计表

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%

根据以上信息，解答下列问题：

(1)、填空：a＝， b＝， c＝；

(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

(3)、根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异.

查看试题解析

23. 如图，在平面直角坐标系 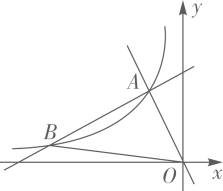$x O y$ 中，一次函数 $y = \frac{1}{2} x + 5$ 和 $y = - 2 x$ 的图象相交于点 $A$ ，反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A$ .

(1)、求反比例函数的表达式；

(2)、设一次函数 $y = \frac{1}{2} x + 5$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象的另一个交点为 $B$ ，连接 $O B$ ，求 $Δ A B O$ 的面积.

查看试题解析
24. 某校举办“创建全国文明城市”知识竞赛，计划购买甲、乙两种奖品共30件．其中甲种奖品每件30元，乙种奖品每件20元．

(1)、如果购买甲、乙两种奖品共花费800元，那么这两种奖品分别购买了多少件？

(2)、若购买乙种奖品的件数不超过甲种奖品件数的3倍，如何购买甲、乙两种奖品，使得总花费最少？

查看试题解析
25. 如图，点P、Q分别是等边 $Δ A B C$ 边AB、BC上的动点（端点除外），点P、点Q以相同的速度，同时从点A、点B出发．

(1)、如图1，连接AQ、CP求证： $Δ A B Q ≅ Δ C A P$

(2)、如图1，当点P、Q分别在AB、BC边上运动时，AQ、CP相交于点M， $∠ Q M C$ 的大小是否变化？若变化，请说明理由；若不变，求出它的度数

(3)、如图2，当点P、Q在AB、BC的延长线上运动时，直线AQ、CP相交于M， $∠ Q M C$ 的大小是否变化？若变化，请说明理由；若不变，求出它的度数．

查看试题解析
26. 如图，抛物线 $y = a x^{2} + b x + 4$ 交x轴于 $A (- 3 ， 0)$ ， $B (4 ， 0)$ 两点，与y轴交于点C ， AC ， BC ． M为线段OB上的一个动点，过点M作 $P M ⊥ x$ 轴，交抛物线于点P ，交BC于点Q ．

(1)、求抛物线的表达式；

(2)、过点P作 $P N ⊥ B C$ ，垂足为点N ．设M点的坐标为 $M (m ， 0)$ ，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？

(3)、试探究点M在运动过程中，是否存在这样的点Q ，使得以A ， C ， Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．

查看试题解析

课外阅读时间（小时）	0.5	1	1.5	2
人数	2	3	4	1