福建省三明市2021年初中毕业班教学质量检测数学试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 2020年6月23日,我国的北斗卫星导航系统(BDS)星座部署完成,其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为( )A、 0.215×108 B、2.15×107 C、2.15×106 D、21.5×1062. 下列几何体中,俯视图为三角形的是( )A、
 B、
B、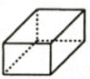 C、
C、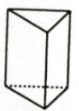 D、
D、 3. 如图,在▱ABCD中,对角线AC,BD相交于点O,E是BC的中点,若OE=3,则AB的长为( )
3. 如图,在▱ABCD中,对角线AC,BD相交于点O,E是BC的中点,若OE=3,则AB的长为( ) A、3 B、6 C、9 D、124. 实数a在数轴上对应点的位置如图所示,若实数b满足-a<b<a,则b的值不可能是下列四个数中的( )
A、3 B、6 C、9 D、124. 实数a在数轴上对应点的位置如图所示,若实数b满足-a<b<a,则b的值不可能是下列四个数中的( ) A、1 B、0 C、-1 D、-25. 下列运算正确的是( )A、 B、 C、 D、6. 为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图 (每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A、1 B、0 C、-1 D、-25. 下列运算正确的是( )A、 B、 C、 D、6. 为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图 (每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( ) A、中位数在60分~70分之间 B、中位数在70分~80分之间 C、中位数在80分~90分之间 D、中位数在90分~100分之间7. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,下列结论错误的是( )
A、中位数在60分~70分之间 B、中位数在70分~80分之间 C、中位数在80分~90分之间 D、中位数在90分~100分之间7. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,下列结论错误的是( ) A、AC=OD B、BC=BD C、∠AOD=∠CBD D、∠ABC=∠ODB8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,在等边△ABC中,点D和点B关于直线AC对称,连接CD,过D作DE⊥BC,交BC的延长线于点E,若CE=5,则BE的长为( )
A、AC=OD B、BC=BD C、∠AOD=∠CBD D、∠ABC=∠ODB8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,在等边△ABC中,点D和点B关于直线AC对称,连接CD,过D作DE⊥BC,交BC的延长线于点E,若CE=5,则BE的长为( )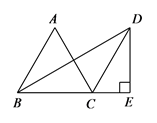 A、10 B、15 C、 D、10. 已知抛物线y=-x2+(6-2m)x-m2+3的对称轴在y轴的右侧,当x>2时,y的值随着x值的增大而减小,点P是抛物线上的点,设P的纵坐标为t,若t≤3,则m的取值范围是( )A、m≥ B、 ≤m<3 C、m<3 D、1≤m<3
A、10 B、15 C、 D、10. 已知抛物线y=-x2+(6-2m)x-m2+3的对称轴在y轴的右侧,当x>2时,y的值随着x值的增大而减小,点P是抛物线上的点,设P的纵坐标为t,若t≤3,则m的取值范围是( )A、m≥ B、 ≤m<3 C、m<3 D、1≤m<3二、填空题
-
11. 分解因式:x2﹣4= .
12. 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B坐标为(4,3),则tan∠AOB的值为. 13. 今年某果园随机从甲、乙、丙三个品种的枇杷树中各选了5棵,每棵产量的平均数 (单位:千克)及方差S2(单位:千克2)如表所示:
13. 今年某果园随机从甲、乙、丙三个品种的枇杷树中各选了5棵,每棵产量的平均数 (单位:千克)及方差S2(单位:千克2)如表所示:甲
乙
丙
45
45
42
S2
1.8
2.3
1.8
明年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是.
14. 如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,扇形的圆心角∠AOB=120°,半径为9m,则扇形的弧长是m. 15. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为.
15. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为. 16. 如图,在Rt△ABC中,∠ACB=90°,AB=8,直线AB经过原点O,点C在y轴上,AC交x轴于点D,CD:AD=4:3,若反比例函数 经过A,B两点,则k的值为.
16. 如图,在Rt△ABC中,∠ACB=90°,AB=8,直线AB经过原点O,点C在y轴上,AC交x轴于点D,CD:AD=4:3,若反比例函数 经过A,B两点,则k的值为.
三、解答题
-
17. 解不等式组:18. 如图,AC为正方形ABCD的对角线,E为AC上一点,且AE=AB,过E作EF⊥AC,交BC于点F.求证:BF=EF.
 19. 先化简,再求值: ,其中a= .20. 如图,在△ABC中,点D在AB边上,且AD:AB=2:3.
19. 先化简,再求值: ,其中a= .20. 如图,在△ABC中,点D在AB边上,且AD:AB=2:3. (1)、在AC边求作点E,使AE:AC=2:3;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若△ABC的周长为12,求△ADE的周长.21. 如图,点M,N在以AB为直径的⊙O上, ,弦MN交AB于点C,BM平分∠ABD,直线EF过点M,且EF⊥BD,垂足为F.
(1)、在AC边求作点E,使AE:AC=2:3;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若△ABC的周长为12,求△ADE的周长.21. 如图,点M,N在以AB为直径的⊙O上, ,弦MN交AB于点C,BM平分∠ABD,直线EF过点M,且EF⊥BD,垂足为F. (1)、求证:EF是⊙O的切线;(2)、若CM=5,CN=6,求BN的长.22. 某校为改善办学条件,计划购进A,B两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:
(1)、求证:EF是⊙O的切线;(2)、若CM=5,CN=6,求BN的长.22. 某校为改善办学条件,计划购进A,B两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:规格
线下
线上
单价(元/个)
运费(元/个)
单价(元/个)
运费(元/个)
A
300
0
260
20
B
360
0
300
30
(1)、如果在线下购买A,B两种书架共20个,花费6720元,求A,B两种书架各购买了多少个;(2)、如果在线上购买A,B两种书架共20个,且购买B种书架的数量不少于A种书架的2倍,请设计出花费最少的购买方案,并计算按照这种方案购买线上比线下节约多少钱.23. 某款热销净水器使用寿命为十年,过滤功能由核心部件滤芯来实现.在使用过程中,滤芯需要不定期更换,滤芯每个200元,若在购买净水器的同时购买滤芯,则滤芯可享受5折优惠(使用过程中如需再购买无优惠).如图是根据100位客户所购买的该款净水器在十年使用期内更换滤芯的个数绘制成的频数分布直方图 (每位客户购买一台). (1)、以这100位客户所购买的净水器在十年使用期内更换滤芯的个数为样本,估计一台净水器在十年使用期内更换滤芯的个数大于10的概率;(2)、假设每位客户在购买净水器的同时购买滤芯10个,计算这100位客户所购买的净水器在十年使用期内购买滤芯所需总费用的平均数.24. 在△ABC和△ADE中,AC=BC,AD=AE,∠ACB=∠DAE=90°,点E在AB上,点F在EB上,∠BCF=∠BDE.
(1)、以这100位客户所购买的净水器在十年使用期内更换滤芯的个数为样本,估计一台净水器在十年使用期内更换滤芯的个数大于10的概率;(2)、假设每位客户在购买净水器的同时购买滤芯10个,计算这100位客户所购买的净水器在十年使用期内购买滤芯所需总费用的平均数.24. 在△ABC和△ADE中,AC=BC,AD=AE,∠ACB=∠DAE=90°,点E在AB上,点F在EB上,∠BCF=∠BDE. (1)、如图①,若E是AB中点,CE延长线交BD于点G,求证:△CEF≌△BEG;(2)、如图②,若E不是AB中点,
(1)、如图①,若E是AB中点,CE延长线交BD于点G,求证:△CEF≌△BEG;(2)、如图②,若E不是AB中点,①求证:CF= BD;
②求证:EF=BF.
25. 已知抛物线的对称轴为直线x=2,且经过点A(0,3)和点B(3,0).(1)、求抛物线的解析式;(2)、点C坐标为(2,- ),过点D(0,- )作x轴的平行线l,设抛物线上的任意一点P到直线l 的距离为d,求证:PC=d;(3)、点E在y轴上(点E位于点A下方),点M,N在抛物线上(点M,N均不同于点A,点M在点N左侧),直线EM,EN与抛物线均有唯一公共点,直线MN交y轴于点F,求证:点A为线段EF的中点.