福建省2021年数学中考精准模拟试卷(三)
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 世界文化遗产—长城的总长约为 ,数据2100000用科学记数法可表示为( )A、 B、 C、 D、3. 在数轴上,表示实数 的点如图所示,则 的值可以为( )
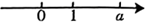 A、-4.5 B、-0.5 C、0 D、0.54. 如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( )
A、-4.5 B、-0.5 C、0 D、0.54. 如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( ) A、70° B、80° C、90° D、100°5. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:
A、70° B、80° C、90° D、100°5. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:调查问卷 ________年________月________日
你平时最喜欢的一种体育运动项目是( )(单选)
A. B. C. D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是( )
A、①②③ B、①③⑤ C、②③④ D、②④⑤6. 如图,图2是图1中长方体的三视图,若该长方体主视图的面积是 ,左视图的面积是 ,则其俯视图的面积是( )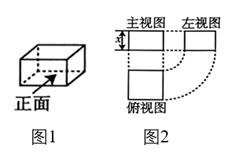 A、 B、 C、 D、7. 若 ,则 的值为( )A、-2 B、-1 C、0 D、8. 下列性质中,等腰三角形具有而直角三角形不一定具有的是 ( )A、两边之和大于第三边 B、有一个角的平分线垂直于这个角的对边 C、有两个锐角的和等于90° D、内角和等于180°9. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )
A、 B、 C、 D、7. 若 ,则 的值为( )A、-2 B、-1 C、0 D、8. 下列性质中,等腰三角形具有而直角三角形不一定具有的是 ( )A、两边之和大于第三边 B、有一个角的平分线垂直于这个角的对边 C、有两个锐角的和等于90° D、内角和等于180°9. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )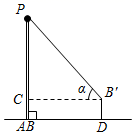 A、 米 B、 米 C、 米 D、 米10. 已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )A、16 B、15 C、9 D、7
A、 米 B、 米 C、 米 D、 米10. 已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )A、16 B、15 C、9 D、7二、填空题
-
11. 计算: .12. 在一个不透明的盒子里,装有10个红球和5个蓝球,每个球除颜色外都相同,从中任意摸出一个球,摸到蓝球的概率是.13. 不等式x+3>5的解集为 .14. 在半径为12的圆中, 圆心角所对的弧长是.15. 在平面直角坐标系中有一个轴对称图形只有一条对称轴,其中点 和点 是这个图形上的一对称点,若此图形上另有一点 ,则点 的对称点的坐标是.16. 二次函数 ,当 时, 的最小值为1,则 的取值范围是.
三、解答题
-
17. 先化简,再求值: ,其中 .18. 解分式方程: .19. 如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交边 , 于点 , ;
②分别以点 , 为圆心,大于 的相同长度为半径作弧,两弧交于点 ;
③作射线 交 于点 .
(1)、根据上述步骤补全作图过程(要求:规作图,不写作法,保留作图痕迹);(2)、如果 , ,那么 的面积与 的面积的比值是.20. 如图,在足够大的空地上有一段长为 的旧墙 ,某人利用旧墙和木栏围成一个矩形菜园 ,其中 .已知矩形菜园的一边靠墙,修筑另三边一共用了 木栏.若所围成的矩形菜园的面积为 ,求 的长.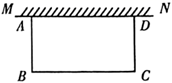 21. 如图, 内接于 , ,动点 , 分别在边 , 上,且 .求证: .
21. 如图, 内接于 , ,动点 , 分别在边 , 上,且 .求证: .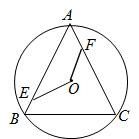 22. 某公司生产某种产品,如果该产品年返修率不超过千分之一,则其生产部门当年考核优秀,现有该公司2012~2019年的相关数据如下表所示:
22. 某公司生产某种产品,如果该产品年返修率不超过千分之一,则其生产部门当年考核优秀,现有该公司2012~2019年的相关数据如下表所示:年份
2012
2013
2014
2015
2016
2017
2018
2019
年生产数量 万台
2
3
4
5
6
7
10
11
该产品的年利润 百万元
2.1
2.75
3.5
3.25
3
4.9
6
6.5
年返修数量/台
21
22
28
65
80
65
84
88
参考数据: ,
, .
其中下角标1~8分别对应2012~2019年.
注:年返修率 .
(1)、该公司的生产部门在2012~2019这八年中总共获得次考核优秀;(2)、从表中数据可以发现2016年的数据偏差较大,如果去掉2016年的数据,试用剩下的数据求出年利润 (百万元)的平均数.23. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,即 ;由周长为m,得2(x+y)=m,即y=-x+ .满足要求的(x,y)应是两个函数图象在第象限内交点的坐标.
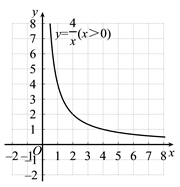
(2)、画出函数图象函数 (x>0)的图象如图所示,而函数y=-x+ 的图象可由直线y=-x平移得到.请在同一直角坐标系中直接画出直线y=-x.
 (3)、平移直线y=-x,观察函数图象
(3)、平移直线y=-x,观察函数图象在直线平移过程中,交点个数有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论 若能生产出面积为4的矩形模具,则周长m的取值范围为.24. 如图1, 的面积为1,点 , , 和 分别在边 , , 上, , , , .设 ,图形 的面积为 .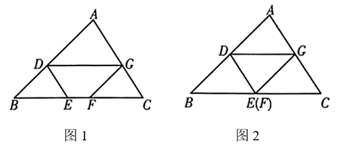 (1)、如图2,当点 和点 重合时,求 与 的值;(2)、如图1,当点 和点 不重合时,求 的最大值.25. 在平面直角坐标系 中,直线 与 轴, 轴分别交于 、 两点.抛物线 经过点 .(1)、如果抛物线 经过点 ,求该抛物线的解析式;(2)、如果抛物线 的顶点 位于 内.
(1)、如图2,当点 和点 重合时,求 与 的值;(2)、如图1,当点 和点 不重合时,求 的最大值.25. 在平面直角坐标系 中,直线 与 轴, 轴分别交于 、 两点.抛物线 经过点 .(1)、如果抛物线 经过点 ,求该抛物线的解析式;(2)、如果抛物线 的顶点 位于 内.①求 的取值范围;
②将该抛物线平移,平移后的抛物线仍经过点 ,此时点 的对应点 坐标为 ,平移后的抛物线与线段 是否还存在其它交点?若存在,请求出交点坐标;若不存在,请说明理由.