重庆市2020-2021学年九年级下学期数学第二阶段考试试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 以下各数中，比 $- 1$ 小的数是（）

A、2 B、0 C、 $- \frac{1}{2}$ D、-2

查看试题解析
2. 据中央广播电视总台中国之声《全国新闻联播》报道，最新数据显示，2020年我国农产品加工业营业收入超过23.2万亿元，较上年增长5.2%将23.2万用科学记数法表示为（）

A、 $0.232 \times 10^{3}$ B、 $23.2 \times 10^{4}$ C、 $2.32 \times 10^{5}$ D、 $2.32 \times 10^{4}$

查看试题解析
3. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 分式 $\frac{x - 3}{x + 1}$ 的值是 $0$ ，则 $x$ 的值为（）

A、3 B、1 C、-1 D、-3

查看试题解析
5. 如图，已知 $B C$ 是 $⊙ O$ 的直径，点 $A ， D$ 在 $⊙ O$ 上，若 $∠ A C B = 32 °$ ，则 $∠ A D C$ 的大小为（）

A、 $68^{\circ}$ B、 $62^{\circ}$ C、 $58^{\circ}$ D、 $52^{\circ}$

查看试题解析
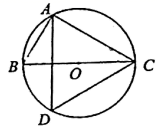6. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $x^{6} \div x^{3} = x^{3}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $\sqrt{x} + \sqrt{y} = \sqrt{x y}$

查看试题解析
7. 下列命题中，是真命题的是（）

A、对角线相等的四边形是平行四边形 B、对角线互相垂直的平行四边形是矩形 C、菱形的对角线相等 D、有一组邻边相等的平行四边形是菱形

查看试题解析
8. 如图，已知， $Δ A B C$ 和 $Δ A' B' C'$ 是位似图形，点 $О$ 是位似中心， $A A' = 2 O A ，$ 若 $Δ A B C$ 的面积为2，则 $Δ A' B' C'$ 的面积为（）

A、4 B、8 C、12 D、18

查看试题解析
9. 清明假期，小明和小亮一起去爬山踏青，感受春的味道.小明和小亮分别选择了两条不同的路线登顶，如图，小明从 $A$ 点出发水平直行到达了 $B$ 点，然后沿坡度为 $i = 0.75 ： 1$ 的斜坡 $B C$ 走500米到达 $C$ 点处，再从 $C$ 点出发水平直行120米到达 $D$ 点，最后从 $D$ 点沿着坡度为 $i = 5 ： 12$ 的斜坡走520米登顶到达 $E$ 点，而小亮选择了从 $A$ 点直接沿着斜坡 $A E$ 登顶 $E$ 点，已知小亮在山顶 $E$ 点测得山脚 $A$ 点的俯角为 $22^{\circ}$ ，则 $A B$ 的长度约为（）米（参考数据： ${sin22}^{o} \approx 0 {.37，cos22}^{o} \approx 0 {.93，tan22}^{o} \approx 0 .40$ ）

A、230米 B、240米 C、250米 D、260米

查看试题解析
10. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{3 x - 1}{2} < x + 2 \\ 5 x - 2 \geq x + a \end{array}$ ，有且仅有3个整数解，且关于 $x$ 的分式方程 $\frac{a x - 2}{x - 1} + \frac{3}{1 - x} = 1$ 有正数解，则所有满足条件的整数 $a$ 的和为（）

A、12 B、13 C、14 D、15

查看试题解析
11. 如图，已知在 $△ A B C$ 中，点 $E$ 是 $B C$ 边上一点，连接 $A E$ ，将 $Δ A B E$ 沿 $A E$ 翻折，得到 $Δ A E B' ， A B$ 交 $B C$ 中点 $D$ .若 $A C = 6 ， B E = 2 ， A D = 3 D B'$ ，若 $S_{Δ D E B^{'}} = 1$ ，求点 $B$ 到线段 $A C$ 的距离（）

A、 $\frac{25}{9}$ B、3 C、 $\frac{28}{9}$ D、4

查看试题解析
12. 如图，矩形 $O A B C$ 在以 $О$ 为原点的平面直角坐标系中，且它的两边 $O A ， O C$ 分别在 $x$ 轴、 $y$ 轴的正半轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与 $B C$ 交于点 $D$ ，与 $A B$ 相交于点 $E$ ，若 $B D = 2 C D ，$ 且 $Δ O D E$ 的面积为4，则 $k$ 的值为（）

A、 $\frac{8}{3}$ B、3 C、4 D、 $\frac{10}{3}$

查看试题解析

二、填空题

13. 计算 ${(\sqrt{2})}^{0} - | - 2 |$ 的结果是.

查看试题解析
14. 将直线 $y = 2 x - 1$ 向上平移2个单位长度，平移后直线的解析式为.

查看试题解析
15. 一个盆子中有若干个红球和8个白球，这些球除了颜色外都相同，再往该盒子中放入4个相同的红球，摇匀后从中随机摸出一个球，若摸到红球的概率是则盒子中原有的红球个数为.

查看试题解析
16. 如图，已知 $A B$ 是 $⊙ O$ 的直径，半径 $O A = 2 ， A C$ 是 $⊙ O$ 的切线，连接 $O C$ 交 $⊙ O$ 于点 $D ，$ 连接 $B D$ .若 $∠ O D B = 30 ° ，$ 则图中阴影部分的面积为.（结果保留）

查看试题解析
17. 五一劳动节假期，小明一家开车去旅游景区游玩，他们从家里出发驾车匀速行驶，出发30分钟后，小明发现自己忘记带学生证了，景区学生证票价半价，于是小明一家马上调头回家，把车速提高到了之前的 $\frac{4}{3}$ ，到家后小明从拿学生证到重新出发用时10分钟，然后他们以 $70 km/h$ 的速度匀速出发赶往景区，中途不停歇，已知小明到景区的距离 $y$ 千米与小明出发的时间 $x$ 分钟的函数关系如图所示，则小明一家从最初出发开始，到最后达到景区整个过程共用时分钟.

查看试题解析
18. 今年春节某超市组装了甲、乙两种礼品盆，他们都是由 $a, b, c$ 三种零食组成，其中甲礼品盒装有3千克 $a$ 零食，1千克 $b$ 零食，1千克 $c$ 零食，乙礼品盒装有2千克 $a$ 零食，2千克 $b$ 零食，2千克 $c$ 零食，甲、乙两种礼品盒的成本均为盆中 $a, b, c$ 三种零食的成本之和.已知每千克 $a$ 的成本为10元，乙种礼品盒的售价为60元，每盒利润率为25%甲种每盒的利润率为50%当甲、乙两种礼盒的销售利润率为 $\frac{1}{3}$ 时，该商场销售甲、乙两种礼盒的数量之比是.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(x - 2 y)}^{2} - y (3 x + 4 y)$

(2)、 $(\frac{10 - 6 m}{m - 1} + m + 1) \div \frac{m^{2} - 3 m}{m - 1}$

查看试题解析
20. 如图， $A B // C D ， A D$ 与 $B C$ 相交于点 $E$ .

(1)、尺规作图：作 $∠ B A D$ 的平分线 $A F$ ，交 $B C$ 于点 $F$ ，交 $C D$ 的延长线于点 $G$ .（要求：不写做法，只保留作图痕迹，并标明字母）

(2)、求证： $D A = D G$ .

查看试题解析

21. 近年来，儿童青少年近视问题受到社会广泛关注.日前，国家卫健委发布《儿童背少年防控近视手册》，分别针对幼儿园、小学生、中学生量身定制了不同版本的个性化防控近视方案.某校为了了解本校学生的视力情况，现抽取学校七、八年级的部分学生进行视力筛查，根据视力检查结果对学生的视力情况进行打分，满分100分.本次视力筛查，分别从七、八年级学生中各抽取了20人进行检测，现对学生视力成绩的数据进行整理和分析.

视力成绩得分用 $x$ 表示，数据共分 $6$ 组：

$A : 40 \leq x < 50$ ； $B : 50 \leq x < 60$ ； $C : 60 \leq x < 70$ ； $D : 70 \leq x < 80, E : 80 \leq x < 90, F : 90 \leq x \leq 100$ .

经过对七、八年级这 $40$ 名学生成绩的整理，绘制了表格如下：

年级	平均数	中位数	众数
七年级	74.1	$a$	$b$
八年级	73.8	75.5	83

七年级学生视力成绩的频数分布如下：

成绩等级	人数
$A$	1
$B$	$c$
$C$	3
$D$	5
$E$	6
$F$	3

七年级视力成绩在 $D 、 E$ 两组的分布是： $70, 75, 70, 76, 70, 80, 85, 85, 80, 85, 85$ .

根据以上数据，完成下列问题：

(1)、完成填空：

a =

_；

b =

；

c =

；

(2)、七年级学生共有300人，若视力成绩在80分及以上为优秀，请估计七年级学生视力优秀的学生有多少人？

(3)、根据以上数据，你觉得七、八年级学生哪个年级的学生视力水平相对较好？请说明理由.

查看试题解析

22. 探究函数的性质可以扩展我们的数学思维.小明正在探究函数

y = a | x - 1 | + b (a ， b

为常数）的性质.下面是小明的探究过程，请补充完整，并解决相关问题：

(1)、列表：

$x$	···	-3	-2	-1	0	1	2	3	4	···
$y$	···	9	7	5	3	1	3	5	$e$	···

(2)、如图，在平面直角坐标系中，根据表格的数据描点、连线，画出该函数的图象；

(3)、观察函数图象，写出该函数图象的其中一条性质；

(4)、当

a | x - 1 | + b > 3

时，直接写出

x

的取值范围.

查看试题解析

23. 材料一：若一个三位数各个数位上的数字之和为9的倍数，则称这个数为“长久数”.
例如：126是“长久数”，因为 $1 + 2 + 6 = 9 ，$ $9$ 是 $9$ 的倍数.658不是“长久数”，因为 $6 + 5 + 8 = 19 ， 19$ 不是9的倍数.

材料二：三位数 $M = \bar{a b c}$ ，若满足 $a > b > c$ 且 $a + c = 2 b$ ，则称 $M$ 为“递减数”.

(1)、判断963是否为“长久数”和“递减数”？并说明理由；

(2)、求出既是“长久数”又是“递减数”的所有三位数.

查看试题解析
24. 已知，在 $R t Δ A B C$ 中， $∠ B C A = 90^{°}$ .点 $D$ 为边 $B C$ 延长线上一动点，过点 $D$ 作 $B E ⊥ B A$ 于点 $E$ 并交 $A C$ 于点 $G$ ，连接 $A D$ .点 $F$ 是 $A D$ 的中点.连接 $C F 、 E F 、 C E .$

(1)、如图1，小华研究发现 $∠ B$ 和 $∠ C F E$ 有特定的数量关系，请你认真研究.当 $∠ B = ∠ C F E$ 时，求出 $∠ B$ .

(2)、在（1）小题的结论下，如图2，在点 $D$ 的运动过程中，当 $G C = B C$ 时.式子 $\frac{D E - A E}{C E}$ 的值不变.猜想这个值并证明你猜想的结论.

(3)、在（1）小题的结论下，如图3，过点 $C$ 作 $C M / / D E$ 交 $A B$ 于点 $M$ .在 $M C$ 的延长线上取点 $N$ .使得 $C N = C M$ ，连接 $N F$ .在点 $D$ 的运动过程中，当 $N F$ 取得最小值时，请直接写出 $\sin ∠ F C N$ 的值.

查看试题解析
25. 已知如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 为常数， $a \neq 0$ ）与 $x$ 轴交于点 $A (- 1 ， 0) ， B$ 两点.与 $y$ 轴交于点 $C (0 ， 3)$ 、且抛物线的对称轴为直线 $x = 1$ .

(1)、求抛物线的解析式；

(2)、在以线 $B C$ 上方的抛物线线上有一动点 $P$ ，过点 $P$ 作 $P D ⊥ x$ 轴.垂足为 $D$ ，交直线 $B C$ 于点 $Q$ .是否存在点 $P$ .使得 $P Q + \frac{\sqrt{2}}{2} Q C$ 取得最大值，若存在，请求出它的最大值以及点Р的坐标：若不存在，请说明理由.

(3)、在 $(2)$ 的条件下，将抛物线沿射线 $B C$ 方向平移 $2 \sqrt{2}$ 个单位长度，此时 $P$ 的对应点为 $P' ， M$ 为平移后抛物线对称轴上的一动点.是否存在点 $M$ 使得 $Δ P P' M$ 为等腰三角形，若存在，请求出点 $M$ 的坐标；若不存在，请说明理由.

查看试题解析
26. 魅力重庆，风景秀美，其中享有“鬼城”之称的丰都，世界闻名，吸引大批游客前来.旅游业的发展带动美食经济，中央电视台也曾在“欢乐中国行”栏目中力推“胡辣壳抄手、仙家豆腐乳、麻辣鸡块”等丰都美食.某麻辣鸡店铺推出“到店消费”和“美味到家”两种营销方式，其中“到店消费”按72元/斤付费，“美味到家”按80元/斤，邮费自付的方式付费.2021年2月“到店消费”的销售量比“美味到家”的销售量高12斤，总营业额为17280元.

(1)、求该店2月份“到店消费”和“美味到家”的销售量分别是多少斤？

(2)、为了提高大众知名度，店面决定在3月份搞促销活动，同比2月份“到店消费”的单价下降了 $a %$ ，“美味到家”的单价不变，但购买则送凉拌鸡杂一份，3月底统计发现“到店消费”和“美味到家”销售量同比2月份分别提升了 $25 a %$ 和 $10 a %$ ，总营业额比2月份的总营业额提升了 $15 a %$ 元，求 $a$ 的值.

查看试题解析