河南省郑州市金水区2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 下列图形中,属于中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 一个等腰三角形的两边长分别是3和7,则它的周长为( )A、17 B、15 C、13 D、13或173. 若 ,下列不等式不一定成立的是( )A、 B、 C、 D、4. 不等式组 的解集在数轴上表示正确的是( )A、
A、1个 B、2个 C、3个 D、4个2. 一个等腰三角形的两边长分别是3和7,则它的周长为( )A、17 B、15 C、13 D、13或173. 若 ,下列不等式不一定成立的是( )A、 B、 C、 D、4. 不等式组 的解集在数轴上表示正确的是( )A、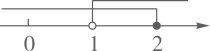 B、
B、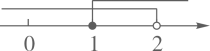 C、
C、 D、
D、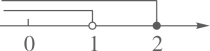 5. 三名同学分别站在一个三角形三个顶点的位置上,他们在玩抢凳子的游戏,要求在他们中间放一个凳子,抢到凳子者获胜,为使游戏公平,凳子应放的最适当的位置在三角形的( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点6. 下列命题中,错误的是( )A、三角形两边之和大于第三边 B、角平分线上的点到这个角两边的距离相等 C、三角形的一条中线能将三角形面积分成相等的两部分 D、等边三角形既是轴对称图形,又是中心对称图形7. 如图, , , 三点在正方形网格线的交点处,若将 绕点 逆时针旋转得到 ,则 点的坐标为( )
5. 三名同学分别站在一个三角形三个顶点的位置上,他们在玩抢凳子的游戏,要求在他们中间放一个凳子,抢到凳子者获胜,为使游戏公平,凳子应放的最适当的位置在三角形的( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点6. 下列命题中,错误的是( )A、三角形两边之和大于第三边 B、角平分线上的点到这个角两边的距离相等 C、三角形的一条中线能将三角形面积分成相等的两部分 D、等边三角形既是轴对称图形,又是中心对称图形7. 如图, , , 三点在正方形网格线的交点处,若将 绕点 逆时针旋转得到 ,则 点的坐标为( ) A、 B、 C、 D、8. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A、 B、 C、 D、8. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )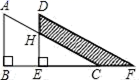 A、20 B、24 C、25 D、269. 如图,在四边形ABCD中, , , , .分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A、20 B、24 C、25 D、269. 如图,在四边形ABCD中, , , , .分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )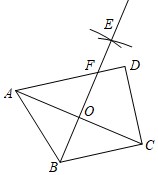 A、 B、4 C、3 D、10. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )
A、 B、4 C、3 D、10. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )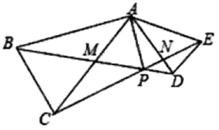 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于 长为半径作弧,两弧交于点P.若点C的坐标为( ),则a的值为 .
 12. 如图,在 中, , ,BD平分 ,CD平分 , ,且EF过点D,则 的周长是.
12. 如图,在 中, , ,BD平分 ,CD平分 , ,且EF过点D,则 的周长是.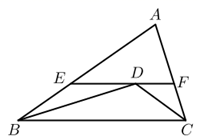 13. 若关于 的不等式组 无解,则 的取值范围是.14. 对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,﹣1}=﹣1,若关于x的函数y=min{2x﹣1,﹣x+3},则该函数的最大值为.15. 如图,在 中, ,将 绕点 旋转 到 ,边 和边 相交于点 ,边 和边 相交于 ,当 为等腰三角形时,则 .
13. 若关于 的不等式组 无解,则 的取值范围是.14. 对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,﹣1}=﹣1,若关于x的函数y=min{2x﹣1,﹣x+3},则该函数的最大值为.15. 如图,在 中, ,将 绕点 旋转 到 ,边 和边 相交于点 ,边 和边 相交于 ,当 为等腰三角形时,则 .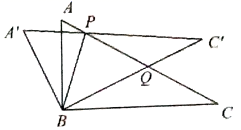
三、解答题
-
16. 解不等式组 ,并求它的所有整数解的和.17. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,坐标分别为 , , .
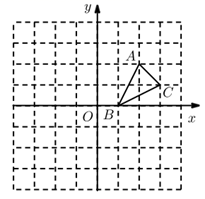 (1)、画出 关于x轴对称的 ;(2)、画出将 绕原点O逆时针旋转90°所得的 ;(3)、 与 成中心对称图形吗?若成中心对称图形,直接写出对称中心的坐标.18. 已知在 中, , 在 上, 在 的延长线上, 交 于 ,且 ,求证: .
(1)、画出 关于x轴对称的 ;(2)、画出将 绕原点O逆时针旋转90°所得的 ;(3)、 与 成中心对称图形吗?若成中心对称图形,直接写出对称中心的坐标.18. 已知在 中, , 在 上, 在 的延长线上, 交 于 ,且 ,求证: .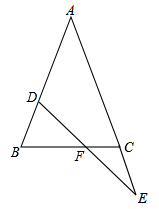 19. 如图,直线y=x+3分别与x轴、y轴交于点A、C , 直线y=mx+ 分别与x轴、y轴交于点B、D , 直线AC与直线BD相交于点M(﹣1,b)
19. 如图,直线y=x+3分别与x轴、y轴交于点A、C , 直线y=mx+ 分别与x轴、y轴交于点B、D , 直线AC与直线BD相交于点M(﹣1,b) (1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.20. 如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.证明:
(1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.20. 如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.证明: (1)、△ABD≌△ACE(2)、BD⊥CE.21. 学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.(1)、求A,B两种奖品的单价;(2)、学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的 .请设计出最省钱的购买方案,并说明理由.22. 阅读材料:
(1)、△ABD≌△ACE(2)、BD⊥CE.21. 学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.(1)、求A,B两种奖品的单价;(2)、学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的 .请设计出最省钱的购买方案,并说明理由.22. 阅读材料:对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)、已知 ,若 ,则当 时, 有最小值,最小值为;(2)、已知 ,若 ,则 取何值时, 有最小值,最小值是多少?(3)、用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?23. 探究:如图1和图2,四边形 中,已知 , ,点 、 分别在 、 上, .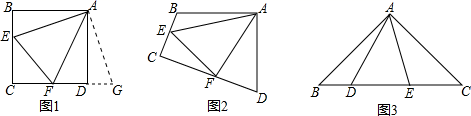 (1)、①如图1,若 、 都是直角,把 绕点 逆时针旋转90°至 ,使 与 重合,直接写出线段 、 和 之间的数量关系 ▲ ;
(1)、①如图1,若 、 都是直角,把 绕点 逆时针旋转90°至 ,使 与 重合,直接写出线段 、 和 之间的数量关系 ▲ ;②如图2,若 、 都不是直角,但满足 ,线段 、 和 之间①中的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(2)、拓展:如图3,在 中, , ,点 、 均在边 上,且 ,若 ,求 的长.