山东省枣庄市台儿庄区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列说法正确的是( )A、同旁内角互补 B、在同一平面内,若a⊥b,b⊥c,则a⊥c C、对顶角相等 D、一个角的补角一定是钝角3. 的值为( )A、 B、 C、 D、4. 如图,AB CD,AD⊥AC,∠BAD=35°,则∠ACD=( )
 A、35° B、45° C、55° D、70°5. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
A、35° B、45° C、55° D、70°5. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、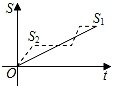 B、
B、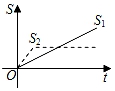 C、
C、 D、
D、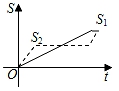 6. 下列各正方形中的四个数之间都有相同的规律,根据此规律, 的值为( )
6. 下列各正方形中的四个数之间都有相同的规律,根据此规律, 的值为( )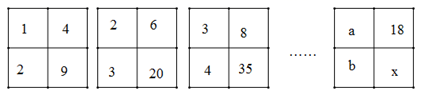 A、135 B、153 C、169 D、1707. 若 , ,则 的值为( )A、0 B、2 C、3 D、48. 如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线 上,斜边AB平分 ,交直线GH于点E,则 的大小为( )
A、135 B、153 C、169 D、1707. 若 , ,则 的值为( )A、0 B、2 C、3 D、48. 如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线 上,斜边AB平分 ,交直线GH于点E,则 的大小为( ) A、 B、 C、 D、9. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、10. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A、 B、 C、 D、9. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、10. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )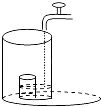 A、
A、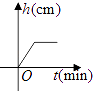 B、
B、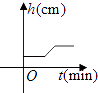 C、
C、 D、
D、 11. 若3×9m×27m=311 , 则m的值为( )A、4 B、3 C、5 D、212. 如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是( )
11. 若3×9m×27m=311 , 则m的值为( )A、4 B、3 C、5 D、212. 如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是( ) A、30 B、20 C、60 D、40
A、30 B、20 C、60 D、40二、填空题
-
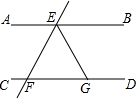
13. 若实数m,n满足 ,则 .14. 如果 能写成一个完全平方的形式,那么k等于;若 ,那么a的值为 .15. 如图,AB∥CD , 直线EF分别交AB , CD于点E , F , EG平分∠BEF , 若∠EFG=64°,则∠EGD的大小是 .
 16. 在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是.17. 若 ,则 .18. 设 , , 是同一平面内三条互相平行的直线,已知 与 的距离是 , 与 的距离是 ,则 与 的距离等于 .
16. 在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是.17. 若 ,则 .18. 设 , , 是同一平面内三条互相平行的直线,已知 与 的距离是 , 与 的距离是 ,则 与 的距离等于 .三、解答题
-
19. 计算(1)、(2)、(3)、(4)、20. 化简求值(1)、 ,其中 , .(2)、 ,其中 ,21. 司机小王开车从A地出发去B地送信,其行驶路s与行驶时间t之间的关系如图所示,当汽车行驶若干小时到达C地时,汽车发生了故障,需停车检修,修理了几小时后,为了按时赶到B地,汽车加快了速度,结果正好按时赶到,根据题意结合图回答下列问题:
 (1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从A地到C地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?22. 观察以下等式:
(1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从A地到C地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?22. 观察以下等式:(x+1)(x2﹣x+1)=x3+1
(x+3)(x2﹣3x+9)=x3+27
(x+6)(x2﹣6x+36)=x3+216
…
(1)、按以上等式的规律,填空:(a+b)()=a3+b3(2)、利用多项式的乘法法则,说明(1)中的等式成立.(3)、利用(1)中的公式化简:(x+y)(x2﹣xy+y2)﹣(x+2y)(x2﹣2xy+4y2)23. 如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H , ∠C=∠EFG , ∠CED=∠GHD .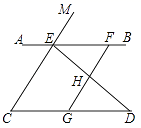 (1)、求证:AB∥CD;(2)、试判断∠AED与∠D之间的数量关系,并说明理由;(3)、若∠EHF=100°,∠D=30°,求∠AEM的度数.
(1)、求证:AB∥CD;(2)、试判断∠AED与∠D之间的数量关系,并说明理由;(3)、若∠EHF=100°,∠D=30°,求∠AEM的度数.