吉林省长春市2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 下列方程是一元一次方程的是( )A、 B、 C、 D、2. 若 是关于 的二元一次方程 的解,则a的值是( )A、1 B、2 C、3 D、43. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、4. 将方程 去分母得到 ,错在( )A、分母的最小公倍数找错 B、去分母时漏乘项 C、去分母时分子部分没有加括号 D、去分母时各项所乘的数不同5. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、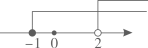 D、
D、 6. 用加减消元法解二元一次方程组 时,下列方法中无法消元的是( )A、①×2﹣② B、②×(﹣3)﹣① C、①×(﹣2)+② D、①﹣②×37. 根据图中给出的信息,下面所列方程正确的是( )
6. 用加减消元法解二元一次方程组 时,下列方法中无法消元的是( )A、①×2﹣② B、②×(﹣3)﹣① C、①×(﹣2)+② D、①﹣②×37. 根据图中给出的信息,下面所列方程正确的是( )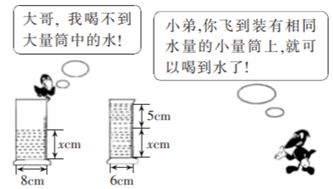 A、 B、 C、 D、8. 从甲地到乙地有一段上坡路与-段平路.如果保持上坡速度为3km/h,平路速度为4km/h,下坡速度为5km/h,那么从甲地到乙地需54min,从乙地到甲地需42min.求甲地到乙地的路程.小玲将这个实际问题转化为二元一次方程组问题,设从甲地到乙地上坡路x km,平路ykm,她已经列出一个方程 ,则另一个方程正确的是( )A、 B、 C、 D、
A、 B、 C、 D、8. 从甲地到乙地有一段上坡路与-段平路.如果保持上坡速度为3km/h,平路速度为4km/h,下坡速度为5km/h,那么从甲地到乙地需54min,从乙地到甲地需42min.求甲地到乙地的路程.小玲将这个实际问题转化为二元一次方程组问题,设从甲地到乙地上坡路x km,平路ykm,她已经列出一个方程 ,则另一个方程正确的是( )A、 B、 C、 D、二、填空题
-
9. 若关于x的方程 的解是 ,则a的值为 .10. 已知方程5x﹣y=7,用含x的代数式表示y,y=
11. “x与5的差不小于x的2倍”用不等式表示为 .12. 关于x的方程3x﹣2m=1的解为正数,则m的取值范围是 .13. 已知关于x、y的方程 的解满足 ,则a的值为.14. 我国古代数学著作《算学启蒙》中有这样一个学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,根据题意,可列方程为 .
三、解答题
-
15. 解方程:16. 解二元一次方程组:17. 解方程组:18. 解不等式:
解:去分母,得
…
(1)、请完成上述解不等式的余下步骤.(2)、解题回顾:本题“去分母”这一步的变形依据是(填“A”或“B”).A.不等式两边都乘以(或都除以)同一个正数,不等号的方向不变.
B . 不等式两边都乘以(或都除以)同一个负数﹐不等号的方向改变.
19. 已知关于x的方程 的解比方程 的解大2.求m值.20. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中有一道题,原文是:“今三人共车,两车空;二人共车,九人步.间人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?21. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .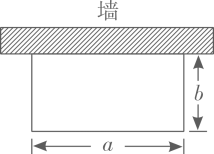 (1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.22. 一般情况下 不成立,但有些数可以使得它成立,例如: .我们称使得 成立的一对数m、n为“相伴数对”,记为 .(1)、若 是“相伴数对”,则 .(2)、若 是“相伴数对”,请用含n的代数式表示m.(要求写过程)(3)、在(2)的条件下,求代数式 的值.23. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件,B种物品45件,共需1140元;如果购买A种物品45件,B种物品30件,共需840元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共600件,总费用不超过7000元,那么A种防疫物品最多购买多少件?24. 如图,已知点A在数轴上对应的数为a,点B对应的数为b,A与B之间的距离记作AB.
(1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.22. 一般情况下 不成立,但有些数可以使得它成立,例如: .我们称使得 成立的一对数m、n为“相伴数对”,记为 .(1)、若 是“相伴数对”,则 .(2)、若 是“相伴数对”,请用含n的代数式表示m.(要求写过程)(3)、在(2)的条件下,求代数式 的值.23. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件,B种物品45件,共需1140元;如果购买A种物品45件,B种物品30件,共需840元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共600件,总费用不超过7000元,那么A种防疫物品最多购买多少件?24. 如图,已知点A在数轴上对应的数为a,点B对应的数为b,A与B之间的距离记作AB.
已知a=-2,b比a大12,
(1)、则B点表示的数是;(2)、设点P在数轴上对应的数为x,当PA-PB=4时,求x的值;(3)、若点M以每秒1个单位的速度从A点出发向右运动,同时点N以每秒2个单位的速度从B点向左运动.设运动时间是t秒,则运动t秒后,用含t的代数式表示M点到达的位置表示的数为 , N点到达的位置表示的数为;
当t为多少秒时,M与N之间的距离是9?